Тема: ДИНАМИКА ТВЁРДОГО ТЕЛА.

ЛЕКЦИЯ 8Д.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА.

1. Дифференциальные уравнения поступательного движения твёрдого тела.

2. Дифференциальные уравнения вращательного движения твёрдого тела.

3. Дифференциальные уравнения плоского движения твёрдого тела.

1. Дифференциальные уравнения поступательного движения твёрдого тела

(8.1)

Здесь m – масса тела, x_c, y_c, z_c - координаты центра масс тела;

проекции внешней силы на оси координат,

проекции главного вектора внешних сил на эти оси.

По дифференциальным уравнениям поступательного движения можно решать два основных типа задач на поступательное движение твёрдого тела:

1. по заданным уравнениям движения твёрдого тела определять главный вектор приложенных к нему внешних сил;

2. по заданным внешним силам, действующим на тело, и начальным условиям движения находить кинематические уравнения движения тела, если известно, что оно движется поступательно.

2. Дифференциальные уравнения вращательного движения твёрдого тела

Момент количества движения т. Мi тела относительно оси Z где ri - радиус окружности, описываемой точкой Мi; - алгебраическая величина вращательной скорости точки Мi. Кинетический момент твёрдого тела относительно оси Z Здесь - момент инерции твёрдого тела относительно оси Z. (8.2) то есть кинетический момент вращающегося твёрдого тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость тела.

Теорема об изменении кинетического момента механической системы

(8.3)

- дифференциальное уравнение вращательного движения твердого тела

По дифференциальному уравнению (8.3) можно решать следующие задачи:

1) по заданному уравнению вращения тела и его моменту инерции J_z определять главный момент внешних сил, действующих на тело

2) по заданным внешним силам, приложенным к телу, по начальным условиям вращения _о и ω_о и по моменту инерции тела J_z находить уравнение вращения тела ;

3) определять момент инерции тела J_z относительно оси вращения, зная величины и .

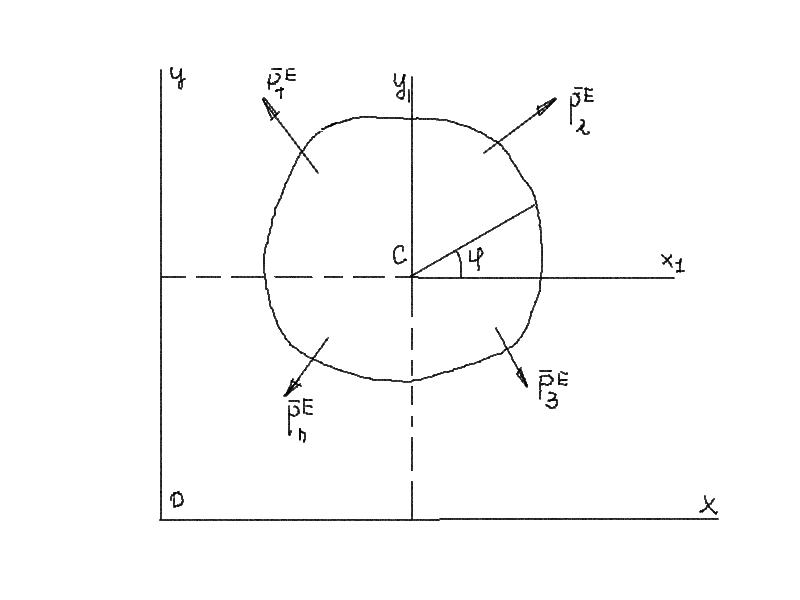
3. Дифференциальные уравнения плоского движения твёрдого тела

- уравнения плоскопараллельного движения твердого тела

Для определения третьего уравнения необходимо последовательно доказать две теоремы:

1. Теорема о зависимости между кинетическими моментами механической системы относительно неподвижного центра и относительно центра масс системы.

2. Теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс. Первая Теорема

Плоское движение разложим на две составляющих:

• относительное движение по отношению к подвижной системе координат.

• переносное движение вместе с подвижной системой отсчёта Сх_1,y_1,z₁, движущейся поступательно

Эти движения называют – поступательным движением системы с центром масс и относительным движением её по отношению к центру масс.

для точки Мi: по определению аналогично - кинетический момент системы относительно центра масс в её относительном движении по отношению к этому центру 1) , где – главный вектор количества движения системы; 2) , Так как при доказательстве теоремы Кенига было получено: ; 3) т.к. так как 4) - кинетический момент системы относительно центра масс в её относительном движении по отношению к этому центру.

теорема

При любом движении механической системы её кинетический момент относительно неподвижного центра равен геометрической сумме: момента относительно этого центра главного вектора количества движения системы, условно приложенного в центре масс, и кинетического момента системы в её относительном движении по отношению к центру масс относительно этого центра.