2.3.2. Сила  функция времени t

В этом случае дифференциальное уравнение движения имеет вид:

. (12)

Так как , то получаем дифференциальное уравнение первого порядка:

,

или

.

Интегрируя это уравнение в соответствующих пределах, имеем:

,

откуда:

. (13)

Интегрируя это уравнение первого порядка, получим x как функцию от t, т.е. найдем искомый закон движения точки.

2.3.3. Сила зависит от положения точки

Задачи, в которых равнодействующая всех сил, приложенных к данной материальной точке, есть функция координаты этой точки. В этом случае дифференциальное уравнение движения точки имеет вид:

, (14)

или:

.

Используя преобразование (10), получим:

,

или:

. (15)

Интегрируя это уравнение в соответствующих пределах, имеем:

. (16)

Из этого равенства определяется скорость V как функция от расстояния х, т.е. , или, разделяя переменныеи проинтегрировав это уравнение первого порядка, найдем зависимость междуx и t. Если является линейной функцией отх, то уравнение (3) будет линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Поэтому для решения этого уравнения можно воспользоваться теорией интегрирования таких дифференциальных уравнений, т.е. составить соответствующее характеристическое уравнение, найти его корни и затем – общее решение данного дифференциального уравнения. Две произвольные постоянные в общем решении находятся по начальным условиям движения точки.

2.3.4. Сила зависит от скорости точки

Такой вид задач будет иметь место при движении точки в сопротивляющейся среде.

В этом случае дифференциальное уравнение движения имеет вид:

, (17)

или, разделяя переменные:

.

Отсюда:

. (18)

Выполняя здесь интегрирование и разрешая полученное уравнение относительно V, находим скорость точки как функцию времени, т.е.

.

Следовательно,

,

и:

. (19)

Это уравнение выражает искомый закон движения точки. Если в задаче требуется найти скорость V как функцию расстояния х, то левую часть уравнения (1) преобразуем:

.

Тогда уравнение (17) принимает вид:

,

или, разделяя переменные:

,

откуда:

. (20)

3. Примеры решения задач

3.1. Примеры решения первой задачи динамики точки

Задача 1. Материальная точка массой m = 0,4 кг совершает гармонические колебания по горизонтальной оси Ох по закону x = 0,2 Sin (/2t) (x выражено в метрах, t – в секундах). Найти силу, действующую на точку в функции оси x.

Решение. Находим проекцию ускорения точки на ось Ох:

(м/с²).

Далее находим проекцию на ось действующей силы:

(Н).

Но по условию задачи , следовательно:(Н).

Рис. 1.

Так как проекция силы на осьОх и координата х движущейся точки противоположны по знаку, то искомая сила направлена вдоль оси Ох к началу координат О и пропорциональна расстоянию от движущейся точки до начала координат.

Задача 2. Лифт весом G поднимается с помощью каната. Канат навернут на барабан радиуса R, вращающийся вокруг неподвижной горизонтальной оси по закону . Определить натяжение каната как функцию высоты подъемаh.

Решение. Так как лифт совершает поступательное движение, при решении задачи будем рассматривать его как материальную точку. При повороте барабана на угол  лифт поднимается на высоту h = R. На него действует две силы: натяжение каната Т и вес лифта G. Причем T > G, т.к. ускорение лифта направленно вверх.

Составим дифференциальное уравнение движения лифта в проекции на ось х:

,

или:

,

откуда:

Рис. 2.

.

Ускорение лифта найдем из соотношения:

,

или:

.

Следовательно:

.

Задача 3. Материальная точка массой m = 0,5 кг совершает движение согласно уравнениям:

.

Координаты точки выражены в метрах, время – в секундах. Определить величину и направление силы, действующей на точку, в момент времени t = 1c.

Решение. Находим проекции ускорения точки на оси координат:

.

На основании системы (2) находим проекции равнодействующей на оси координат:

.

По системе уравнений (6) находим модуль и направляющие косинусы равнодействующей сил:

.

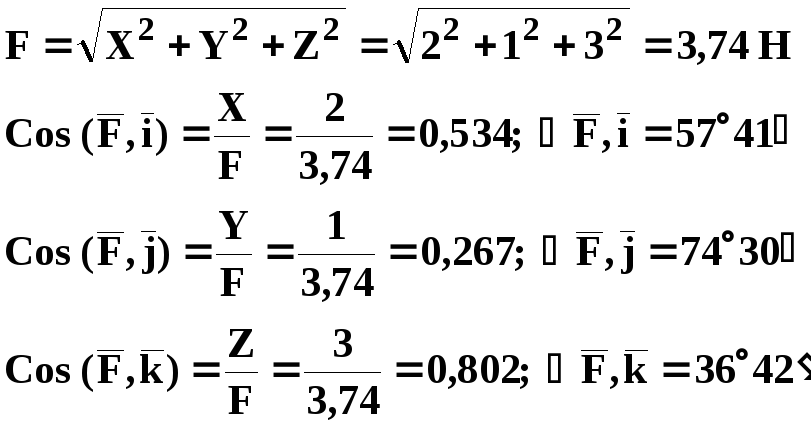Задача 4. Материальная точка массой m = 2 кг описывает криволинейную траекторию по закону (S выражено в метрах, время – в секундах). В данный момент она занимает положение М и имеет скорость V = 3 м/с, радиус кривизны траектории в точке М равен 6 м. Найти в этот момент времени силу, действующую на материальную точку.

Решение. Находим скорость точки и проекции ее ускорения на касательную и главную нормаль траектории:

.

Согласно условию задачи в данный момент времени V = 3 м/с. Определяем время t:

.

Следовательно, в этот момент:

.

Определяем проекции равнодействующей на касательную и главную нормали:

.

Модуль равнодействующей:

Рис. 3.

.