
- •Министерство образования российской федерации
- •Н. Г. Неумоина, а.В.Белов две задачи динамики точки
- •Раздел «динамика»
- •2.2. Первая основная задача динамики точки
- •2.3. Вторая основная задача динамики точки
- •2.3.1. Сила, постоянная по модулю и направлению
- •2.3.2. Сила функция времени t
- •2.3.3. Сила зависит от положения точки
- •2.3.4. Сила зависит от скорости точки
- •3. Примеры решения задач
- •3.1. Примеры решения первой задачи динамики точки
- •Задача 5.Определить натяжение нити математического маятника длинойlи весомG, если качания маятника совершаются согласно уравнению:
- •3.2. Примеры решения второй задачи динамики точки
- •4. Задание на самостоятельную работу
- •5. Контрольные вопросы
- •6. Используемая литература
- •Содержание
- •400131 Волгоград, просп. Им. В.И. Ленина, 28.
- •400131 Волгоград, ул. Советская, 35.
Задача 5.Определить натяжение нити математического маятника длинойlи весомG, если качания маятника совершаются согласно уравнению:
![]() ,
,
где — угол отклонения маятника от вертикали, 0 и k — постоянные величины.
Решение.
К маятнику
приложены: вес G
и реакция нити k.
Покажем на рисунке эти силы, а так же
составляющие ускорения маятника
![]() и
и![]() .
.
Составим
дифференциальное уравнение движения
маятника в проекции на главную нормаль
![]() .
.
![]() .
.
И
Рис.
4.
![]() .
.
Тогда:
![]() ,
,
откуда:
![]() .
.
Так
как по условию
![]() ,
то
,
то
![]() .
.
Окончательно находим:
 . Наибольшее
значение реакции нити наблюдается в
отвесном положении, т.е. когда kt
= n:
. Наибольшее
значение реакции нити наблюдается в
отвесном положении, т.е. когда kt
= n:
![]() .
.
3.2. Примеры решения второй задачи динамики точки
Задача 6. Материальная точка массой m = 0,5 кг движется под действием постоянной силы F = 10 Н. В начальный момент времени скорость точки равна V0 = 2м/с. Определить скорость точки, когда она пройдет расстояние S = 5 м.
Решение. Так как скорость точки требуется найти как функцию расстояния, то по формуле (10) имеем:
![]() ,
,
т. е.:
![]() ,
,
откуда:
![]() м/с.
м/с.
Задача
7. На
материальную точку, совершающую
прямолинейное движение, действует сила
F,
равномерно убывающая с течением времени
и по истечении Т
секунд обращающаяся в нуль. Какой
скорости достигнет точка по истеч
Рис.
5.
![]() .
.
Решение.
Так как сила
![]() ,
действующая на материальную точку,
убывает равномерно с течением времени,
то:
,
действующая на материальную точку,
убывает равномерно с течением времени,
то:
![]() ,
,
где b = const.
В
начальный момент ускорение точки равно
![]() ,
поэтому
,
поэтому![]() .
Кроме того, приt
= T
по условию задачи F
= 0, поэтому:
.
Кроме того, приt
= T
по условию задачи F
= 0, поэтому:
![]() .
.
Отсюда:
![]() ,
,
и:
![]() .
.
Следовательно, дифференциальное уравнение движения точки запишется так:
![]() ,
,
или:
![]() .
.
Интегрируя это уравнение:
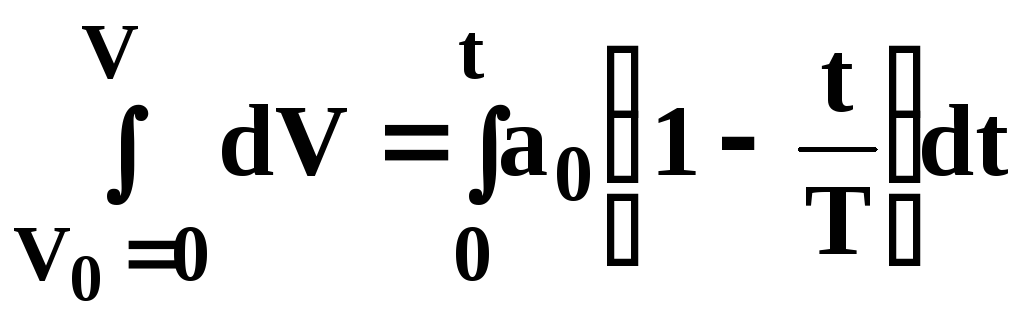 ,
,
получим:
![]() .
.
Так
как
![]() ,
то:
,
то:
![]() ,
,
откуда
![]() .
.
Интегрируя это уравнение в пределах от 0 до x и от 0 до t, находим:
![]() ,
,
![]() .
.
Чтобы найти скорость V1 и пройденный путь x1 к моменту времени Т, достаточно в предыдущих равенствах положить время t = Tc.
Тогда имеем:
![]() ,
,
![]() .
.
Задача 8. Материальная точка М массой m движется прямолинейно по оси Ох. Точка отталкивается от неподвижного центра О силой F, пропорциональной массе m и расстоянию, причем коэффициент пропорциональности равен
k
Рис.
6.
Решение.
Первый способ. По условию задачи
![]() ,
поэтому дифференциальное уравнение
движения имеет вид:
,
поэтому дифференциальное уравнение
движения имеет вид:
![]()
или:
![]() .
.
Так
как в данном случае
![]() ,
то по уравнению (15) имеем:
,
то по уравнению (15) имеем:
![]() ,
,
откуда:
 ,
,
или:
![]() ,
,
т.е.:
![]() ,
,
и:
![]() .
.
Отсюда:
 ,
,
т.е.:
![]() ,
,
или:
![]() .
.
Следовательно:
![]() .
.
Из этого соотношения находим:
![]() ,
,
откуда:
![]() ,
,
или:
![]() .
.
Второй
способ. Так как в данном случае функция
![]() является линейной функцией отх,
то дифференциальное уравнение (15)
является линейным дифференциальным
уравнением второго порядка с постоянными
коэффициентами.
является линейной функцией отх,
то дифференциальное уравнение (15)
является линейным дифференциальным
уравнением второго порядка с постоянными
коэффициентами.
Для решения этого уравнения воспользуемся теорией интегрирования линейных дифференциальных уравнений с постоянными коэффициентами и составим соответствующее характеристическое уравнение:
![]() .
.
Найдем
его корни:
![]() .
Следовательно, общее решение выразится
так:
.
Следовательно, общее решение выразится
так:
![]() .
.
Постоянные С1 и С2 находим по начальным условиям движения. Для этого сначала найдем скорость точки, продифференцировав последнее уравнение по времени:
![]() .
.
В начальный момент согласно условию имеем:
![]() .
.
Следовательно:
![]() ,
,
![]() ,
,
откуда:
С1 = 3, С2 = 2;
таким образом:
![]() .
.
Задача 9. Материальная точка массы m = 0,1 кг движется прямолинейно под действием постоянной силы F = 0,3 Н. Движение происходит в среде, сила сопротивления которой выражается функцией скорости в виде:
![]() ,
,
где V — скорость точки. Найти закон движения точки, если начальная скорость равна нулю.
Р
Рис.
7.
![]() направлена в сторону движения, а сила
направлена в сторону движения, а сила![]() – противоположно скорости.
– противоположно скорости.
В соответствии с уравнением (3) дифференциальное уравнение движения точки имеет вид:
![]() .
.
Так как в данном случае равнодействующая всех приложенных сил есть функция скорости, т.е.:
![]() ,
,
то по уравнению (18) имеем:
 ,
,
откуда:
![]() .
.
Из этого уравнения находим V:
 .
.
Воспользуемся далее уравнением (20) и найдем искомый закон движения точки:
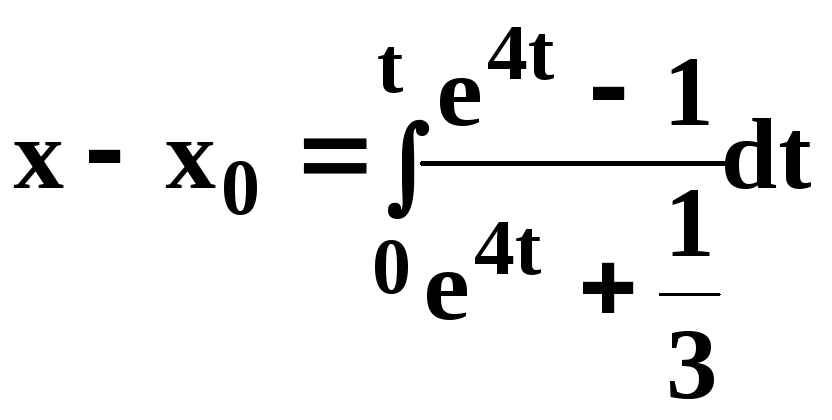 .
.
Чтобы вычислить этот интеграл, сделаем замену переменных:
![]() ,
,
тогда:
 .
.
Следовательно:
![]() .
.
