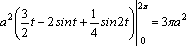Bilety / 33

33. Вычисление длин плоских кривых при помощи определенного интеграла. Длина окружности. Длина арки циклоиды.

3.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой

  . (28)

3.2. Если кривая задана параметрическими уравнениями , где x(t), y(t) - дифференцируемые функции, то длина дуги

. (29)

3.3. Если дуга задана в полярных координатах , , то длина дуги

. (30)

П р и м е р 20. Вычислить длины дуг плоских кривых:

а) ; б) ;

в) , .

Решение. а) Воспользуемся формулой (10). Так как

,

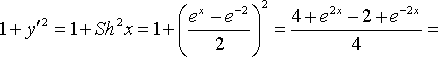
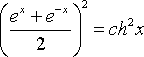то

.

б) Воспользуемся формулой (11). Так как , то.

в) .

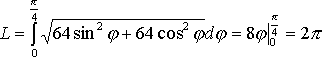Пример 41.4. Найти длину окружности радиуса R.

Решение: Найдем 1/4 часть ее длины от точки (0;R) до точки (R;0) (см. рис. 184). Так как то

Значит, l = 2πR. Если уравнение окружности записать в параметрическом виде х=Rcost, у = Rsint (0≤t≤2π), то

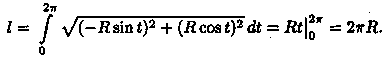
Пример 2. Найти площадь фигуры, ограниченной первой аркой циклоиды , и отрезком оси O_x (рис. 11).

Решение. Точкам O и A соответствуют значения параметра и , поэтому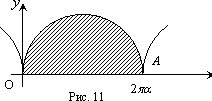