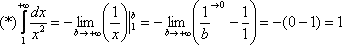Bilety / 30

30.Определение, свойства и вычисление не собственного интеграла, случай бесконечного промежутка. Примеры.

Свойства

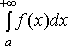1)     Если интеграл  сходиться, С – некоторое число, то интеграл 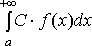 также сходиться и 

2)     Если интегралы 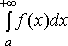 и 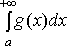 сходятся, то интеграл 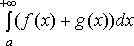 только сходится и

 

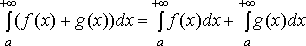
3)     Если функции  и  интегрируемы при , то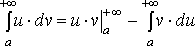 

4)     Пусть функция  непрерывна при , функция  определена, непрерывна и имеет непрерывную производную на промежутке  конечном или бесконечном, где <

Тогда 

_____________________________________________________________________

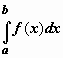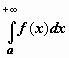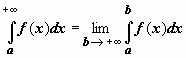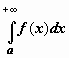Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси  и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла  при  называется несобственным интегралом функции f(x) от a до  и обозначается .  Итак, по определению, . Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.  Примеры: 1. ; этот предел не существует; следовательно, исследуемый интеграл расходится.  2. 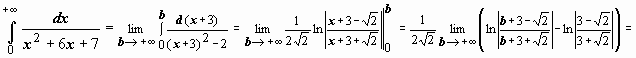; следовательно, интеграл сходится и равен .  Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от  до b :  и в пределах от  до :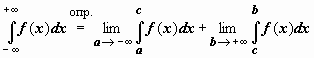. В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Пользуясь свойством аддитивности определённого интеграла, можно показать, что существование конечных пределов и их сумма не зависят от выбора точки c.  Примеры: 3. 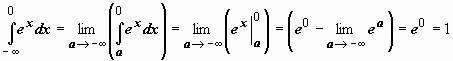. Интеграл сходится.  4.    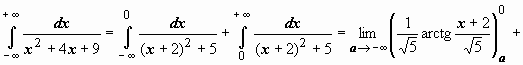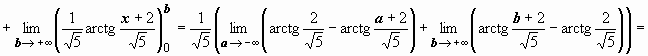следовательно, интеграл сходится и равен .  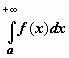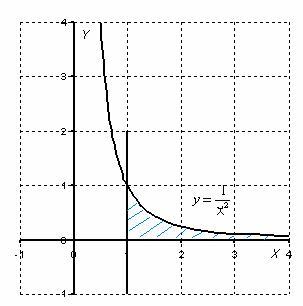Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом:  сходится тогда и только тогда, когда для любого c, удовлетворяющего неравенству c > a, сходится интеграл 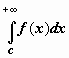 (док-во: так как при a < c < b по свойству аддитивност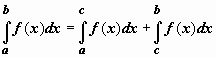и , и 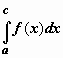 от b не зависит, то конечный предел при  для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства). 

Примеры

Рассмотрим два классических примера:

Пример 1

Вычислить несобственный интеграл или установить его расходимость.

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.

Подынтегральная функция  непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы   и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы  «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».

Если Вам непонятно почему  при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики  и свойства элементарных функций.

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“ Подынтегральная функция  непрерывна на  Несобственный интеграл расходится. “

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией. Этим мы идентифицируем тип несобственного интеграла.

Если Вам встретится интеграл вроде , то с вероятностью, близкой к 100%, можно сказать, что это опечатка. Здесь подынтегральная функция не является непрерывной на промежутке интегрирования , она терпит разрыв в точке . Теоретически и практически допустимо вычислить два несобственных интеграла на полуинтервалах  и , а потом их сложить, но со здравой точки зрения такая вещь выглядит довольно абсурдно. Опечатка.

Иногда вследствие той же опечатки несобственного интеграла может вообще не существовать, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть интервала интегрирования вообще не войдёт вобласть определения подынтегральной функции.

Всегда смотрим и записываем, является ли подынтегральная функция непрерывнойна интервале интегрирования.

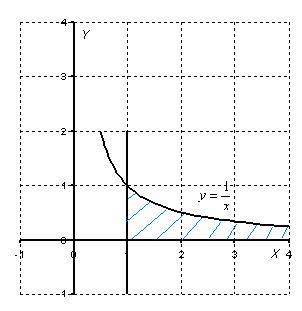
Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция  непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :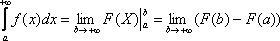

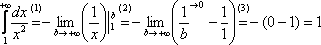
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что  при  (Господа, это уже давно нужно  понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“ Подынтегральная функция непрерывна на