Bilety / 23

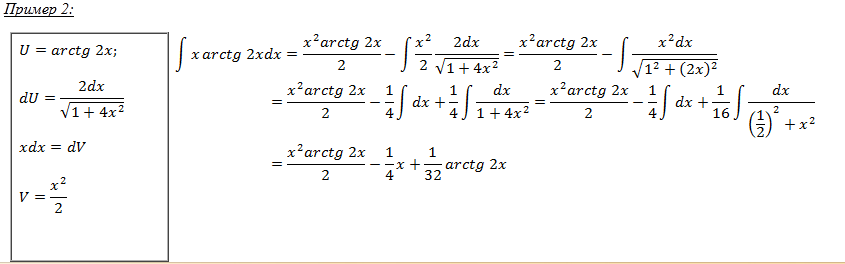
Пример.

Найти неопределенный интеграл 

Решение.

Найдем этот неопределенный интеграл методом интегрирования по частям. В качестве функции u(x) возьмем ln(x), а в качестве d(v(x)) оставшуюся часть подынтегрального выражения, то есть dx.

Имеем, , где .

Дифференциал функции u(x) есть , а функция v(x) – это .

ЗАМЕЧАНИЕ: константу С при нахождении функции v(x) считают равной нулю.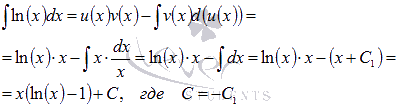

Теперь все подставляем в формулу интегрирования по частям:

Ответ:.

Пример.arcsin

Найти неопределенный интеграл .

Решение.

Используем метод интегрирования по частям. В качестве функции u(x)возьмем arcsin(2x), d(v(x)) = xdx, тогда .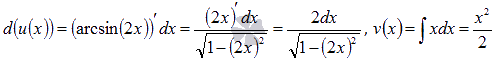

Применяем формулу: 

Таким образом, пришли к равенству: 

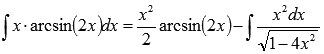
Найдем отдельно полученный интеграл .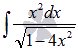

Применим метод интегрирования по частям: 

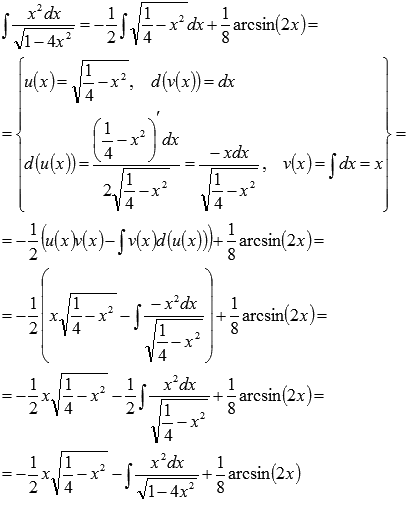
Таким образом, получили равенство .

Интеграл в правой части равенства получился таким же как и в левой части. Перенесем его из правой части в левую:

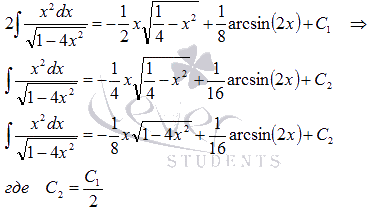
Теперь можно возвращаться к началу примера: 

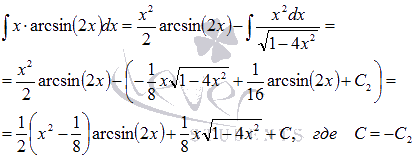
Ответ:

.