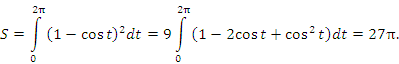Bilety / 32

32. Вычисление площадей плоских фигур при помощи определенного интеграла. Площадь элипса и круга. Площадь арки циклойды.

Пример 4

Вычислить площадь круга, ограниченного окружностью, заданной уравнением 

 – это окружность с центром в начале координат радиуса .

Выполним чертёж:

Сначала вычислим площадь круга с помощью известной школьной формулы. Если радиус круга , то его площадь равна: 

Для того чтобы вычислить площадь круга с помощью определенного интеграла, необходимо из уравнения окружности  выразить функцию «игрек» в явном виде:

Верхняя полуокружность задается уравнением  Нижняя полуокружность задается уравнением 

Особые параноики, как я, могут подставить несколько точек окружности в эти уравнения, и убедиться в справедливости вышеизложенных утверждений.

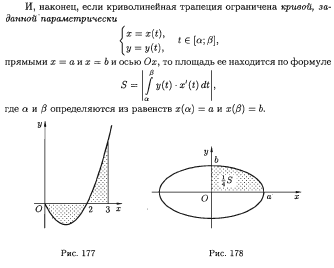
Как вычислить площадь круга? В данном примере круг симметричен относительно начала координат, поэтому достаточно вычислить площадь сектора в 1-ой четверти (заштрихован синим цветом), затем результат умножить на 4.

Таким образом:

Такой же, но неопределенный интеграл рассматривался в примере 6 урока Сложные интегралы, он решался длительным и трудоёмким методом сведения интеграла к самому себе. Можно пойти тем же путём, но для определенного интеграла существует удобный и эффективный метод тригонометрической замены:

Проведём замену: 

Почему именно такая замена, очень скоро станет понятно, а пока найдем дифференциал:

Выясним, во что превратится корень, я распишу очень подробно:

Если в ходе решения вы не сможете догадаться применить формулу наподобие  , то, увы, схлопочете от преподавателя «приходите в следующий раз».

После преобразования корня отчетливо видно, почему проведена замена , особое внимание обращаю на коэффициент при синусе – «двойке», этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.

Осталось вычислить новые пределы интегрирования: Если , то 

Новый нижний предел интегрирования:  Новый верхний предел интегрирования: 

Таким образом:

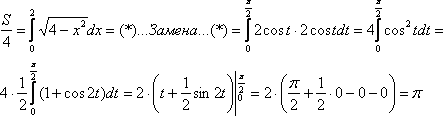
Площадь сектора необходимо умножить на 4, следовательно, площадь всей окружности:

Пример 3.  Найти площадь фигуры, ограниченной осью  0x  и одной аркой циклоиды

            .  Рис. 2. Первая арка циклоиды. Циклоида представляет собой линию, которую описывает точка на ободе катящегося без проскальзывания колеса.

Решение.  Представим интеграл  в терминах переменной  t.  Учитывая, что  x(0)=0,   и  , получаем