2.2. Уравнение Клапейрона-Клаузиуса.

Определение теплоты испарения жидкости

Для равновесия между жидкостью и паром уравнение Клапейрона-Клаузиуса может быть получено следующим образом.

Согласно второму закону термодинамики если система находится в равновесии, то при данных условиях (Р, Т) работа не совершается

Ap = 0; G_ж - G_п = 0; G_ж = G_п(2)

то есть свободные энергии Гиббса чистой жидкости и её пара равны (это условия равновесия).

Изменим одно из условий, определяющих равновесие, например, температуру (то есть нагреем систему на Т), в результате этого установится новое давление, новое равновесие жидкость-пар:

G^'_ж = G^'_п (3)

или G_ж = G_п (4)

Если изменение внешнего параметра произойдет на бесконечно малую величину - dT, то и изобарно-изотермические потенциалы изменятся на бесконечно малую величину:

dG_ж=dG_п (5)

Изобарно-изотермический потенциал представляет собой свободную энергию системы и является функцией давления и температуры:

dG=VdP–SdT (6)

поэтому с его помощью можно установить количественную зависимость между давлением насыщенного пара и температурой.

После подстановки (6) в (5) имеем в состоянии равновесия

V_жdP - S_жdT = V_пdP - S_пdT (7)

откуда (8)

где (S_п - S_ж) и (V_п - V_ж) - изменение соответственно энтропии и объема системы при переходе вещества из жидкого в парообразное состояние. Согласно второму закону термодинамики изменение энтропии системы при испарении равно приведенной теплоте испарения

(9)

Подставив выражение (9) в (8) получим

(10)

где ∆H_исп и ∆V_исп - соответственно изменение энтальпии и объема при испарении, аT_кип- температура кипения.

Уравнение (10) называется уравнением Клапейрона-Клаузиуса. Согласно (10) наклон линий на фазовой диаграмме воды (рис. 1) определяется знаком производнойdP/dT или обратной ей величиныdT/dP - характеризующей изменение температуры с увеличением дав­ления.

Из фазовых переходов рассмотрим испарение и плавление. Теплота испарения - перехода жидкой фазы в газообразную положитель­на. Молярной теплотой испаренияназывается количество тепла, затраченное на испарение одного моля жидкого вещества. Объем газа при испарении всегда больше соответствующего объема жидкости, то есть в уравнении (10)V_п > V_ж. ПоэтомуdP/dT, а значит, иdT/dP также всегда положительны (dT/dP > 0). Следовательно, температура испарения всегда повышается с ростом давления (кривая ОКна рис. 1 или см. табл. 1 Приложения). С увеличением температуры давление насыщенного пара над жидкостью возрастает, принимая максимальное значение при критической температуре. Последняя является предельной температурой (например, для воды она равна 374,12^оС) при которой возможно равновесие между жидкой и паровой фазой ве­щества. При более высоких температурах вещество может находиться только в газообразном состоянии, и понятие насыщенного пара теряет свой смысл.

Теплота плавления - перехода твердой фазы в жидкую также всегда положительна.

Рис. 1. Диаграмма состояния воды при невысоких давлениях

Области: 1 - твердая фаза (лед); II- жидкость; III - пар.

Кривые: АО - возгонки; ОК - испарения; ОВ - плавления.

О - тройная точка, отвечающая равновесию трех фаз.

Объем жидкой фазы в общем случае может быть больше или меньше объёма того же количества твердой фазы. Отсюда в соответствии с уравнением (10) вытекает, что величина dP/dT или обратная её величинаdT/dP, может быть положительной или отрицательной. Это значит, что температура плавления может повышаться или снижаться с увеличением давления. ВеличинаdT/dP положительна для большинства веществ. Она имеет отрицательное значение лишь для воды, висмута и немногих других веществ, для которых плотность жидкости при температуре плавления больше плотности твердой фазы (V_ж -V_т) < 0. В связи с этим при увеличении давления температура плавления льда понижается (криваяОВ).

Необходимо отметить, что рассмотренные закономерности справедливы для невысоких давлений.

Уравнение Клапейрона-Клаузиуса (10) можно преобразовать приняв следующие приближения:

1) Поскольку ∆V_исп =(V_п -V_ж) >> 0 (например, для воды мольный объём в парообразном состоянии при н.у. V_п≈ 22400 см², а в жидком состоянииV_ж ≈ 18 см³), то без большой погрешности можно пренебречь величиной V_жи принять, что ∆V_исп ≈ V_п.

2) При не слишком высоких давлениях и температурах (вдали от критических) можно применять уравнение состояния для идеальных газов и к реальным системам. Погрешность, получаемая при этом, оказывается незначительной.

Тогда

(11)

Подставив (11) в (10) получим:

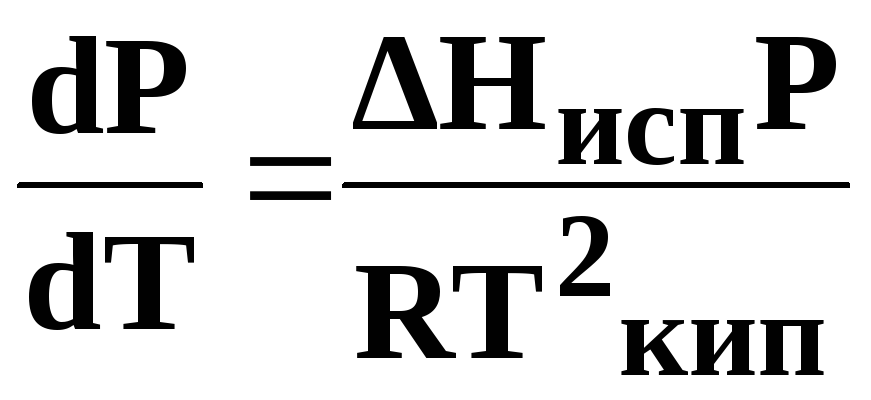(12)

которое после преобразования

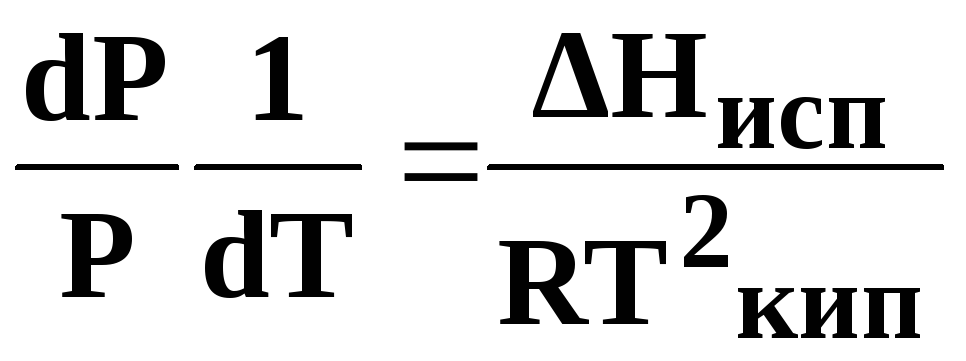(13)

принимает вид

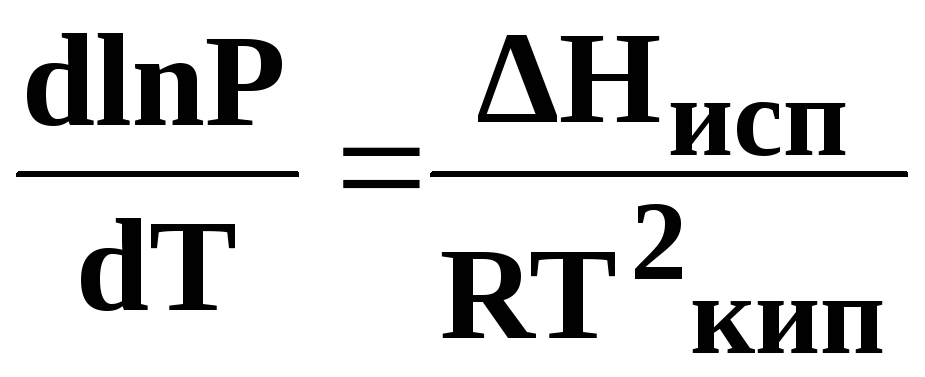(14)

Теплота испарения зависит от температуры: с повышением температуры теплота испарения понижается. При критической температуре теплота испарения равна нулю. Однако при температурах, далеких от критической, изменения ∆Н_испс температурой не очень велики. В не слишком большом интервале температур ∆Н_исп можно считать постоянной.

Интегрирование уравнения Клапейрона-Клаузиуса (14) в пределах температур Т₁ иТ₂, которым отвечают давленияР₁ иР₂ при постоянном значении ∆Н_исп, дает

(15)

или при переходе к десятичным логарифмам

(16)

(R - универсальная газовая постоянная равная 8,314 Дж/моль · К).

Уравнения (15), (16) позволяют рассчитать теплоту испарения. Для этого по экспериментальным данным строят зависимость lnP=f(1/T) илиlgP =f(1/T) и на полученной прямой выбирают две точки (рис. 2). Подставляют соответствующие этим точкам значения логарифма давления и обратной температуры в уравнение (17):

(17)

Значение ∆Н_исппо уравнению (17) зависит от взятого интервала температур и тем ближе к истинному, чем этот интервал меньше. Однако для такого вычисления требуется весьма точное измерение температуры кипения и давления пара.

Для вычисления ∆Н_испв относительно широком интервале температур (50...100^оС) следует выбирать точки, наиболее точно укладывающиеся на прямую lgP=f(1/T).

Температура кипения жидкости, давление пара при данной тем­пературе и теплота испарения являются специфическими константами вещества, значения которых необходимы для многих теоретических и практических расчетов. На основе этих данных можно определять чистоту химических веществ, провести расчет разделения смесей путем перегонки, рассчитать энергетические затраты на испарение жидкости, необходимые для проведения реакции в газовой фазе.