Задание 8

Пример 1. Вычислить модуль циркуляции векторного полявдоль контураГ:

Решение.Для вычисления циркуляции векторного полявдоль замкнутого контураГвоспользуемся формулой (2.4)

Так как задано пространственное векторное поле и пространственный замкнутый контурГ, то переходя от векторной формы записи криволинейного интеграла к координатной форме, получаем

.

Кривая Гзадана как пересечение двух поверхностей: гиперболического параболоидаz = x²–y²+ 2 и цилиндраx²+y²= 1. Для вычисления криволинейного интеграла удобно перейти к параметрическим уравнениям кривойГ:x=cost,y=sint,z= 2 +cos2t, 0 ≤t≤ 2.

Уравнение цилиндрической поверхности можно записать в виде: x=cost,y=sint,z= z. Выражение дляzв параметрических уравнениях кривой получается подстановкойx=cost,y=sintв уравнение гиперболического параболоидаz =2 +cos² t–sin² t= 2 +cos2t.

Так как входящие в параметрические уравнения кривой Гфункцииx(t) =cost,y(t) =sint,z(t) = 2 +cos2tявляются непрерывно дифференцируемыми функциями параметраtприt[0; 2], то находим криволинейный интеграл по формуле (2.6)

Учитывая, что ,,, а также тригонометрические формулы sin 2t= 2sintcost,получаем

так как cos 4 = cos 0 = 1, sin 8 = sin 0 = 0.

Пример 2.Вычислить модуль циркуляции векторного полявдоль контура

Решение.Если одна из поверхностей, при пересечении которых образуется замкнутый контурГ, представляет собой плоскость параллельную одной из координатных плоскостей, то циркуляцию удобно находить, используя формулу Стокса:

где – часть двухсторонней поверхности, ограниченной замкнутым контуромГ, – единичный вектор нормали к поверхностии выбор стороны поверхности и направление обхода контураГсогласованы.

Находим ротор векторного поля по формуле (2.11):

В качестве выбираем верхнюю сторону плоскости z = 1. Тогда и скалярное произведение

.

Подставляя найденное выражение в формулу Стокса, получаем

где S– площадь части поверхности, ограниченной контуромГ. КриваяГзадана как пересечение поверхности эллиптического параболоидаи плоскостиz= 1, то есть представляет собой эллипс, расположенный в плоскостиz= 1 и задаваемый уравнениями

Как известно, площадь эллипса, задаваемого каноническим уравнением вычисляется по формулеS =ab. Поэтому

.

Задание 9

Доказать, что векторное поле потенциально. Найти потенциал поля.

Решение. Докажем, что векторное поле потенциально, используя необходимое и достаточное условие потенциальности векторного поля(2.10)

Найдем по формуле (2.11)

.

Так как , то

Заданное векторное поле потенциально.

Определяем потенциал поля по формуле (2.13)

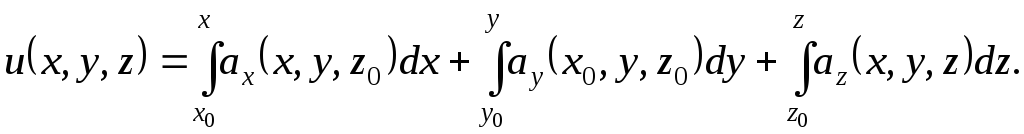
Выбор точки M₀(x₀,y₀,z₀) определяется двумя условиями:

1) в точке M₀векторное поле должно быть определено;

2) интегралы, включающие в формулу (2.13) должны максимально упрощаться,

В данном случае

Задание 1.

Вычислить криволинейный интеграл I рода по дуге L.

1. , гдеL – дуга кривой .

2. , где L – дуга кривой .

3. , где L – дуга эллипса , лежащая в 1 квадранте.

4. , где L – дуга кривой

5. , где L – дуга кривой

6. , где L – дуга кривой между точками О(0,0) и А(π/2,0).

7. где L – контур треугольника с вершинами О(0,0), А(1,0) и В(0,1).

8. где L – дуга кривой .

9. , где L – дуга параболы .

10. , где L – контур прямоугольника с вершинами А(0,0), В(4,0), С(4,2), D(0,2).

11. , где L – дуга кривой .

12. , где L – дуга кривой .

13. , где L – дуга кривой .

14. , где L – дуга кривой между точками А(0,2) и В(1,).

15. , где L – дуга кривой между точками А(0,2) и В(2,).

16. , где L – дуга окружности между точками А(0,5) и В().

17. , где L – отрезок прямой между точками А(0,7) и В(1,10).

18. , где L – дуга кривой между точками О(0,0) и А(4,4).

19. , где L – дуга параболы между точками А(0,1) и В(1,2).

20. , где L – дуга кривой между точками О(0,0) и А(1,1/3).

21. , где L – дуга кривой , между точками А(-3,2) и В(0,1).

22. , где L – отрезок прямой между точками А(0,-5) и В(1,-2).

23. , где L – дуга кривой , отсеченная кривой .

24. , где L – дуга кривой между точками А(0,1) и В(1,1/е).

25. , где L – дуга кривой .

26. , где L – дуга параболы между точками А(0,1) и В(1/2,3/4).

27. , где L – отрезок прямой .

28. , гдеL – дуга окружности между точками А(0,1) и В(1/2,).

29. , где L – дуга кривой между точками А(-2,9) и В(0,5).

30. , где L – дуга кривой .

Задание 2.

Задание 2.

Вычислить криволинейный интеграл I рода по дуге L.

1.

2. .

3. .

4. .

5. .

6. .

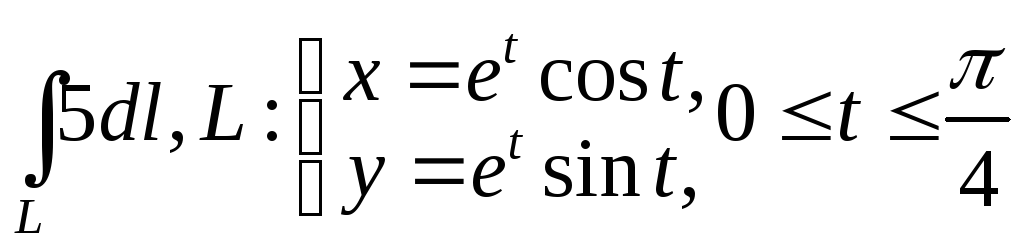7. .

8. .

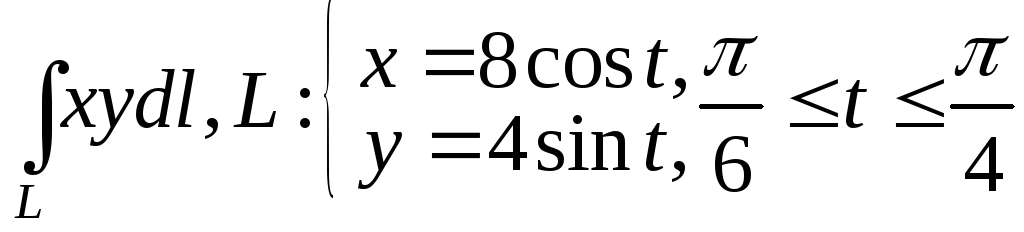9. .

10. .

11. .

12. .

13. .

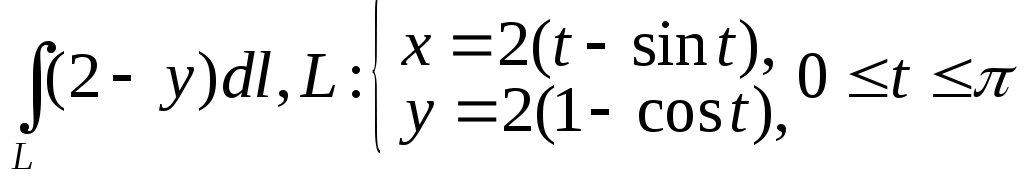14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

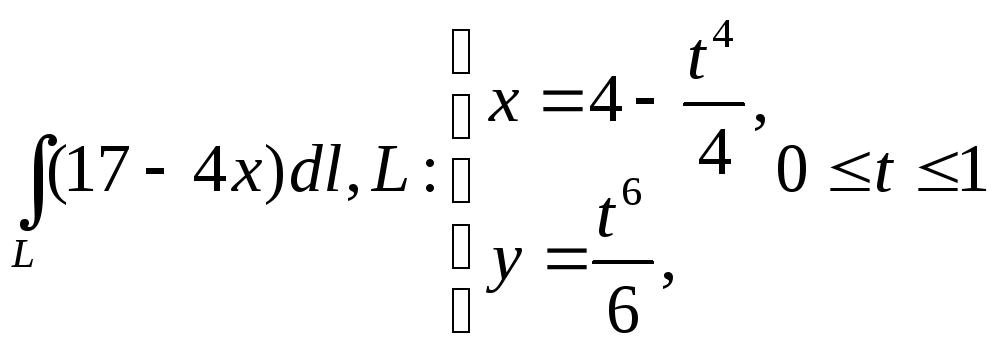22. .

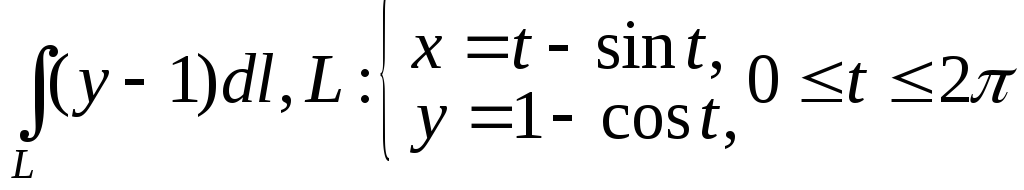23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

Задание 3.

Найти массу дуги линии L с линейной плотностью µ.

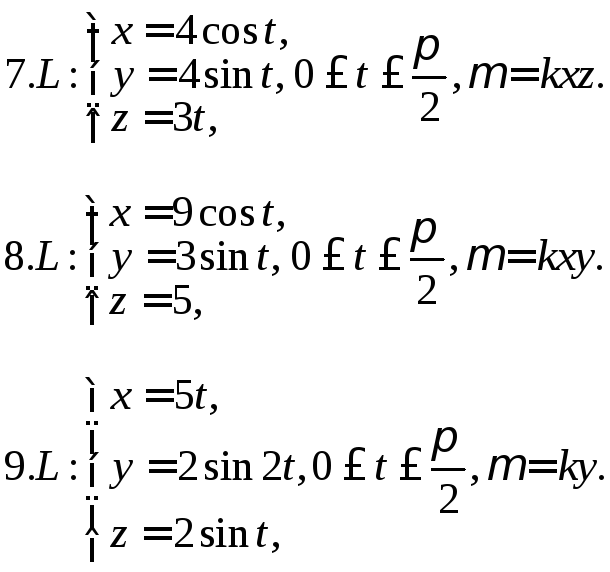
Задание 4.

Вычислить криволинейный интеграл 2 рода по дуге кривой L, где дугой L является:

а) ломаная АВС, б) отрезок АС.

Задание 5.

Вычислить криволинейный интеграл 2 рода по дуге L.

Задание 6.

Вычислить криволинейный интеграл 2 рода по замкнутому контуру С.

где С – контур треугольника с вершинами А(1,1), В(2,2), С(1,3), пробегаемый против часовой стрелки.

где С - контур треугольника с вершинами А(0,0), В(1,1), С(0,3), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(1,1), В(2,2), С(3,1), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(1,1), В(2,3), С(2,5), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(0,0), В(1,0), С(0,1), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(1,1), В(2,3), С(2,5), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(2,2), В(2,5), С(3,5), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(0,0), В(2,2), С(1,3), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(1,1), В(2,2), С(1,3), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(0,0), В(1,1), С(3,0), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(2,0), В(1,1), С(1,0), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(0,-4/3), В(4,0), С(0,4/3), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(1,1), В(2,2), С(1,3), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(0,0), В(1,0), С(1,1),D(0,1), пробегаемый против часовой стрелки.

контур треугольника с вершинами А(-3,-5),

В(-3,5), С(1,1), пробегаемый против часовой стрелки.

Задание 7.

Найти работу силы F при перемещении вдоль линии L от точки М к точке N.

отрезок

отрезок

отрезок

отрезок

отрезок

отрезок

Задание 8.

Вычислить модуль циркуляции векторного поля а вдоль контура F.

Задание 9.

Доказать, что векторное поле а(М) потенциальное. Найти потенциал поля.

список использованной литературы

1. Шипачев В. С. Высшая математика / В. С. Шипачев. – М.: Высш. школа, 2007.

2. Пискунов Н. С. Дифференциальное и интегральное исчисления: учебное пособие для студ. вузов.Т.2. / Н. С. Пискунов. – М.:Интеграл-Пресс, 2004.

3. Письменный Д. Т. Конспект лекций по высшей математике / Д. Т. Письменный. Ч. 2. – М.: Рольф, 2000.

4. Сборник задач по математике для втузов. Специальные разделы математического анализа / под редакцией А. В. Ефимова, Б. П. Демидовича. – М.: Наука, 1986.

5. Краснов М. Л. Векторный анализ / М. Л. Краснов, А. И. Киселев, Г. И. Макаренко. – М.: Наука, 1978.

6. Лунгу К. Н. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу, В. П. Норин, Д. Т. Письменный, Ю. А. Шевченко, Е. Д. Кулагин; под. редакцией С. Н. Федина. – М.: Айрис-пресс, 2006.

7. Данко П. Е. Высшая математика в упражнениях и задачах. Учебное пособие для вузов. Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Мир и образование, 2003.

Марина Израилевна Андреева

Ольга Евгеньевна Григорьева