3. Примеры выполнения заданий Задание 1

Вычислить криволинейный интеграл I рода

где L – дуга кривой , 0 ≤x≤ 1.

Решение. По формуле (1.3) сведения криволинейного интеграла I рода к определенному интегралу в случае гладкой плоской явно заданной кривой:

где y=y(x),x₀≤x≤x₁ – уравнение дугиLкривой интегрирования. В рассматриваемом примереНаходим производную этой функции

и дифференциал длины дуги кривой L

.

Так как

,

то, подставляя в это выражение вместоy, получаем

Преобразуем криволинейный интеграл к определенному:

.

Вычисляем этот интеграл с помощью подстановки . Тогдаt²= 1 +x,x=t²– 1,dx= 2t dt; приx =0t= 1; аx= 1 соответствует. После преобразований получаем

Задание 2

Вычислить криволинейный интеграл 1 рода по дугеLкривойL: x=cos³t,y=sin³ t,.

Решение.Так какL– дуга гладкой плоской кривой, заданной в параметрическом виде, то используем формулу (1.1) сведения криволинейного интеграла 1 рода к определенному:

.

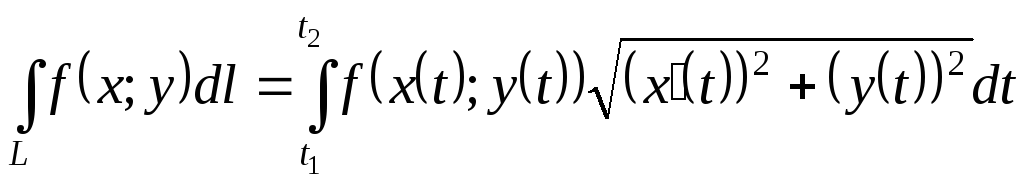В рассматриваемом примере

Найдем дифференциал длины дуги

Найденные выражения подставляем в формулу (1.1) и вычисляем:

Задание 3

Найти массу дуги линии Lс линейной плоскостью.

L:

Решение.Массаm дугиLс плотностью(P) вычисляется по формуле (1.8)

.

Это криволинейный интеграл 1 рода по параметрически заданной гладкой дуге кривой в пространстве, поэтому он вычисляется по формуле (1.2) сведения криволинейного интеграла 1 рода к определенному интегралу:

Найдем производные

и дифференциал длины дуги

Подставляем эти выражения в формулу для массы:

.

Задание 4

Пример 1.Вычислить криволинейный интеграл 2 рода

по дуге L кривой 4x+y²= 4 от точкиA(1; 0) до точкиB(0; 2).

Решение.Плоская дугаLзадана в неявном виде. Для вычисления интеграла удобнее выразитьxчерезy:

и находить интеграл по формуле (2.8) преобразования криволинейного интеграла 2 рода в определенный интеграл по переменной y:

где a_x(x; y) = xy – 1, a_y(x; y) = xy².

С учетом задания кривой

По формуле (2.8) получаем

Пример 2. Вычислить криволинейный интеграл 2 рода

где L– ломанаяABC,A(1; 2),B(3; 2),C(2; 1).

Решение. По свойству аддитивности криволинейного интеграла

Каждый из интегралов- слагаемых вычисляем по формуле (2.7)

где a_x(x;y) =x² +y,a_y(x;y) = –3xy.

Рис. 2

Уравнение отрезка прямой AB:y= 2,y= 0,x₁= 1,x₂= 3. Подставляя в формулу (2.7) эти выражения, получаем:

Для вычисления интеграла

составим уравнение прямой BCпо формуле

где x_B,y_B,x_C,y_C– координаты точекBиС. Получаем

y– 2 =x– 3,y=x– 1,y= 1.

Подставляем полученные выражения в формулу (2.7):

Задание 5

Вычислить криволинейный интеграл 2 рода по дуге L

0 ≤ t≤ 1.

Решение. Так как кривая интегрирования задана параметрически уравнениямиx = x(t),y = y(t),t[t₁;t₂], гдеx(t) иy(t) – непрерывно дифференцируемые функцииtприt[t₁;t₂], то для вычисления криволинейного интеграла второго рода используем формулу (2.5) сведения криволинейного интеграла к определенному для плоской параметрически заданной кривой

.

В рассматриваемом примере a_x(x;y) =y;a_y(x;y) = –2x.

Cучетом задания кривойLполучаем:

Подставляем найденные выражения в формулу (2.5) и вычисляем определенный интеграл:

Задание 6

Пример 1.Вычислить криволинейный интеграл 2 рода по замкнутому контуруC⁺гдеС:y²= 2x,y=x– 4.

Решение.ОбозначениеC⁺указывает, что обход контура осуществляется в положительном направлении, то есть против часовой стрелки.

Проверим, что для решения задачи можно использовать формулу Грина (2.9)

Так как функции a_x(x;y) = 2y–x²;a_y(x;y) = 3x+yи их частные производныенепрерывны в плоской замкнутой областиG, ограниченной контуромC, то формула Грина применима.

.

Для вычисления двойного интеграла изобразим область G, предварительно определив точки пересечения дуг кривыхy²= 2xиy=x– 4, составляющих контурC.

Точки пересечения найдем, решив систему уравнений:

Второе уравнение системы равносильно уравнению x²– 10x+ 16 = 0, откудаx₁= 2,x₂= 8,y₁= –2,y₂= 4.

Итак, точки пересечения кривых: A (2; –2),B (8; 4).

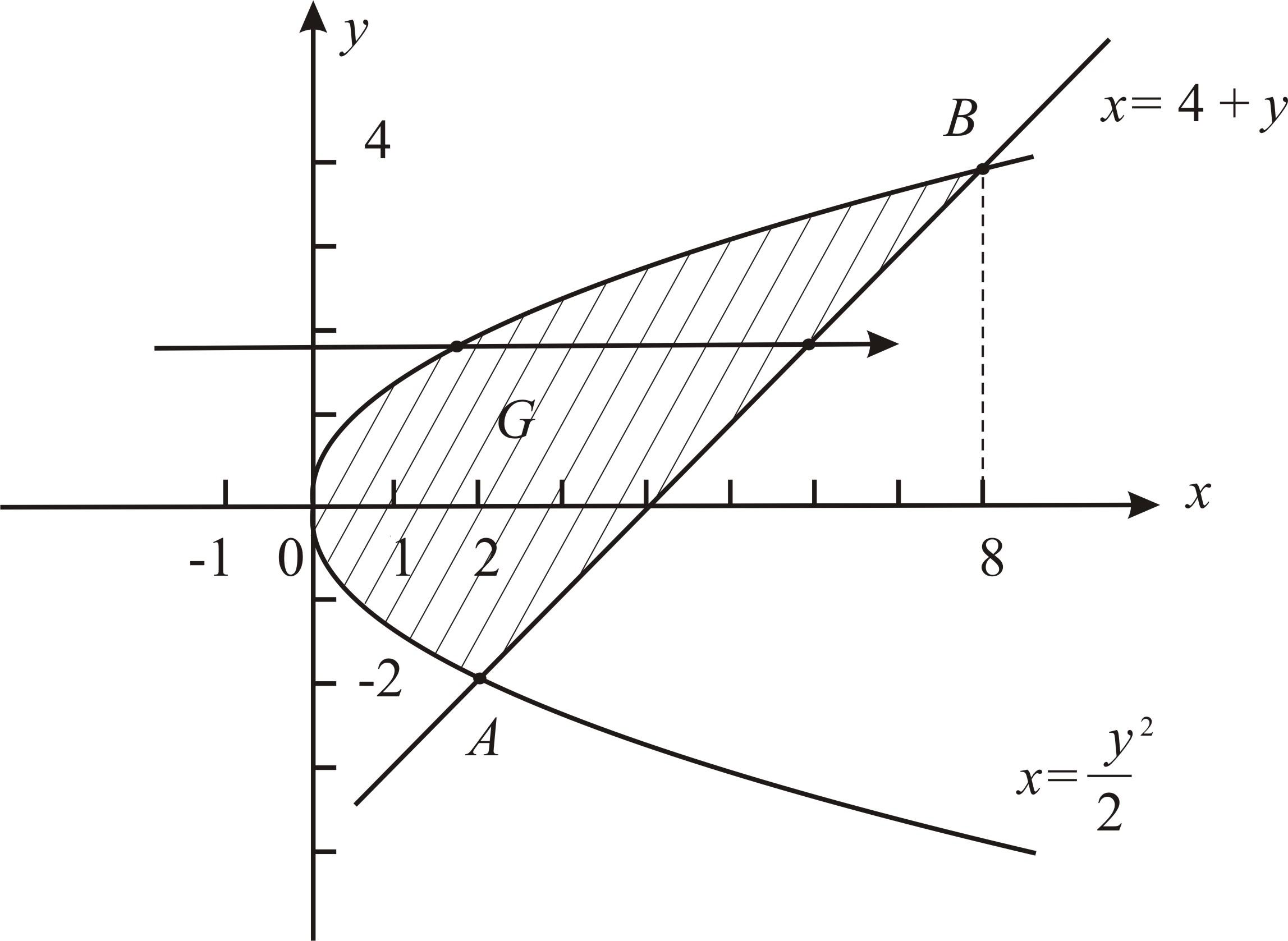
Рис. 3

Так как область G – правильная в направлении осиOx, то для сведения двойного интеграла к повторному спроектируем областьGна осьOYи воспользуемся формулой

.

Так как a= –2,b= 4, x₂(y) = 4+y, то

Пример 2.Вычислить криволинейный интеграл 2 рода по замкнутому контуругдеС– контур треугольника с вершинамиA(0; 0),B(1; 2),C(3; 1).

Решение.Обозначениеозначает, что контур треугольника обходится по часовой стрелке. В случае, когда криволинейный интеграл берется по замкнутому контуру, формула Грина принимает вид

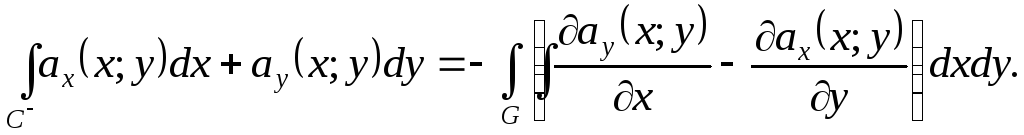
Изобразим область G, ограниченную заданным контуром.

Рис. 4

Функции и частные производныеинепрерывны в областиG, поэтому можно применить формулу Грина. Тогда

Область Gне является правильной в направлении какой-либо из осей. Проведем отрезок прямойx= 1 и представимGв видеG=G₁G₂, гдеG₁иG₂области, правильные в направлении осиOy.

Тогда

Для сведения каждого из двойных интегралов по G₁иG₂к повторному будем использовать формулу

где [a;b] – проекция областиDна осьOx,

y=y₁(x) – уравнение нижней ограничивающей кривой,

y=y₂(x) – уравнение верхней ограничивающей кривой.

Запишем уравнения границ области G₁и найдем

AB: y = 2x, 0 ≤ x ≤ 1; AD: , 0 ≤x ≤ 1.

Составим уравнение границы BCобластиG₂, используя формулу

BC:где 1 ≤x≤ 3.

DC: 1 ≤x≤ 3.

Тогда

Итак,