4.2. Включение постоянного напряжения

в последовательную цепь RLС

Пусть в моментt = 0 в последовательную цепь RLC включается постоянное напряжение U. Второе уравнение Кирхгофа при t > 0 будет таким:

. (1)

Далее можно пойти двумя путями. Либо, продифференцировав (1), заниматься уравнением для тока:

,

где − коэффициент затухания,− собственная частота. Оно точно такое же, как и в предыдущем разделе, только другими будут начальные условия. Либо, подставив в (1) выражение, получить уравнение для напряжения на конденсатореи_С, решить его, а затем уже найти и ток i. Выберем, для определённости, второй путь. Для простоты, опустим у напряжения и_С индекс, т. е. положим и_С ≡ и, . Тогда уравнение (1) примет вид:

. (2)

Как и в предыдущем разделе, решение этого уравнения может быть как колебательным, так и апериодическим, в зависимости от соотношения между параметрами β и ω₀. Рассмотрим вкратце два варианта, с учётом наработок, полученных в предыдущем разделе.

Вариант 1: > 0 (колебательный вариант).

Тогда общим решением уравнения (2) будет функция

. (3)

(здесь последнее слагаемое U – это частное решение неоднородного уравнения (2)).

Коэффициенты А и В находим из начальных условий. Первое начальное условие очевидно: и(0) = 0, откуда получаем: В = −U. Второе начальное условие для можно получить из соотношения: так какi(0) = 0, то и =0.

Это даёт: А = −(β/ω)U. И тогда

. (4)

При слабозатухающем процессе, когда β≪ω₀, это выражение упрощается:

. (5)

Теперь из (4) после некоторых преобразований находим ток:

=. (6)

Видно, что здесь ток ведёт себя точно так же, как и в варианте 1 предыдущего раздела, а вот напряжение на конденсаторе – немного по-другому: его затухающие колебания происходят около уровня U. В первые моменты на конденсаторе возникает перенапряжение, почти в 2 раза превышающее приложенное напряжение U.

Вариант 2: (критический вариант).

Общим решением уравнения (2) в этом случае будет функция

. (6)

Подставив те же начальные условия и(0)=0 и в (6), получим:В=,. И тогда

. (7)

Ток i получаем из (7) после некоторых преобразований и учитывая, что в данном варианте = 1/(LC):

=,

т. е. ток и здесь точно такой же, как и в варианте 2 предыдущего раздела 5.1.

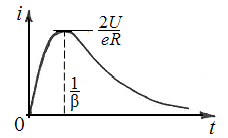
4.3. Воздействие длинными импульсами

на последовательную цепь RLС («звон контура»)

Из разделов 4.1 и 4.2 следует, что если на последовательный контур RLС подавать прямоугольные импульсы достаточно большой длительности:

τ_и ≫ Т= 2π/ω₀,

то, в зависимости от соотношения между β и ω₀, на конденсаторе С будут выделяться следующие картины напряжения:

Причём «звон» в контуре при скачках напряжения на нём будет тем дольше, чем больше добротность контура

.

4.4. Действие очень короткого импульса

на последовательную цепь RLC

Пусть в моментt=0 на последовательный контур RLС подействовали очень коротким прямоугольным импульсом напряжением U, длительностью τ ≪ Т, где Т=1/, т. е.

После действия импульса контур остаётся замкнутым, т. е. внутреннее сопротивление генератора импульсов равно нулю.

Исследуем процесс в контуре после действия такого импульса: i(t) и u_C(t) при t > τ. Рассмотрим два варианта: R < R_кр и R = R_кр.

Решение. Действие на контур очень короткого импульса аналогично удару по шарику математического маятника: сразу после удара потенциальной энергии у шарика ещё нет, но импульс он уже получил.

Здесь аналогично: за время τ ток в катушке стал таким: , а напряжение на конденсаторепри малом τ − ещё практически нулевое.

Таким образом, при t > τ в контуре начнётся свободный процесс при начальных условиях: i(τ) =,u_C(τ) = 0, т. е. .

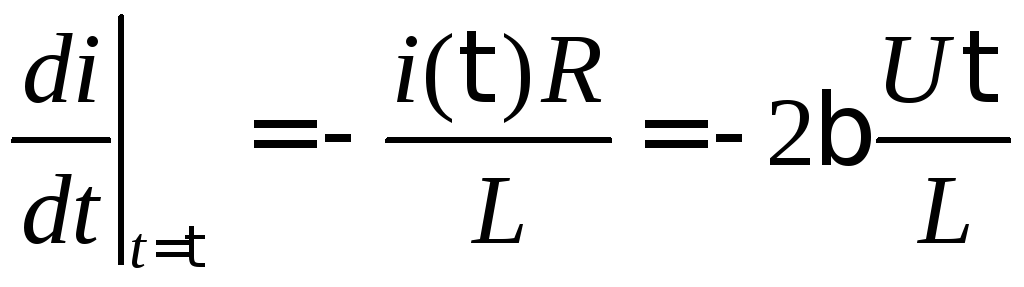ПриR < R_кр ток описывается функцией

, где ,

а при R = R_кр ток ,

а напряжение .

Замечание. Произведение Uτ – это площадь импульса. При τ→0, но Uτ = const, мы имеем δ-функцию.