
- •18 Переходные процессы в простейших цепях Содержание
- •Переходные процессы в простейших цепях
- •1. Понятие о переходных процессах
- •2. Классический метод расчёта переходных процессов в цепях rlc
- •I(t)t→∞→ iчастн.(t).
- •3. Переходные процессы в простейших цепях 1-го порядка
- •3.1. Разряд конденсатора через активное сопротивление
- •3.2. Включение постоянного напряжения
- •3.3. Включение постоянного напряжения
- •3.4. Отключение постоянного напряжения
- •4. Переходные процессы в одноконтурной цепи 2-го порядка
- •4.1. Отключение постоянного напряжения
- •4.2. Включение постоянного напряжения
- •4.3. Воздействие длинными импульсами
- •4.4. Действие очень короткого импульса
- •4.5. Включение синусоидального напряжения
3.1. Разряд конденсатора через активное сопротивление
Разряд предварительно заряженного конденсатора через активное сопротивление (через резистор) является простейшим переходным процессом.
Пусть конденсатор ёмкостью С заряжен до напряжения U. В момент t=0 замыкается ключ К и конденсатор начинает разряжаться через активное сопротивление R. Так как здесь внешнего воздействия нет, то в цепи будет только свободный процесс.
В ыбрав
направление обхода, запишем для этой
цепи второе уравнение Кирхгофа:
ыбрав
направление обхода, запишем для этой
цепи второе уравнение Кирхгофа:
uR−uC=0,
или
iR−uC=0. (1)
А так как для
конденсатора ток i
здесь является разрядным,
то
![]() ,
и тогда
,
и тогда![]() ,
(2)
,
(2)
или
![]() ,
,
где
![]() −постоянная
времени
RC-цепочки.
−постоянная
времени
RC-цепочки.
Общее решение этого однородного уравнения имеет вид (проинтегрировать самостоятельно; однако, решение уравнения такого типа надо знать):
![]() ,
,
где А
– коэффициент, определяемый начальным
условием,
т.е.
![]() − напряжением на конденсаторев
первый момент после замыкания
ключа К.
Так как, по условию, до замыкания
напряжение
− напряжением на конденсаторев
первый момент после замыкания
ключа К.
Так как, по условию, до замыкания
напряжение
![]() ,
а напряжение на конденсаторе скачком
измениться не может (это привело бы к
тому, что
,
а напряжение на конденсаторе скачком
измениться не может (это привело бы к
тому, что![]() ,
тогда как в уравнении (2)иС
– конечно), то
,
тогда как в уравнении (2)иС
– конечно), то
![]() (это второе правило
коммутации).
(это второе правило
коммутации).
Это даёт: А=U, и, следовательно,
![]()
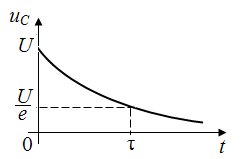 .
(3)
.
(3)
Отсюда видно, что τ – это время, за которое напряжение на конденсаторе убывает в е раз:
 2,7.
2,7.
Реально время переходного процесса оценивается примерно в 3τ, когда напряжение уменьшается в е3 = 20 раз, или когда до установившегося значения осталось лишь 1/20 = 5 % от исходного напряжения U.
Пример. Пусть С=1 мкФ, R=1 кОм. Тогда время переходного процесса Δtперх.=3τ=3RC=3 мс.
Теперь легко получить закон убывания тока в цепи:
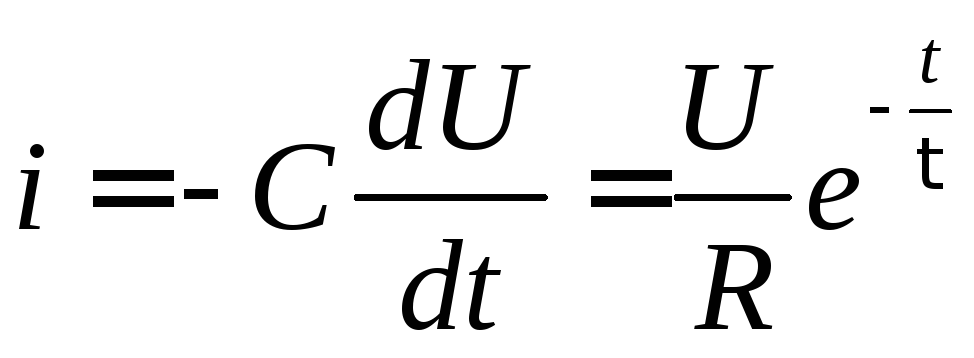 .
.
Видно, что он точно такой же, как и закон убывания напряжения.
3.2. Включение постоянного напряжения
в последовательную цепь RC
Рассмотрим теперь процесс заряда конденсатора через активное сопротивление R от генератора с постоянным напряжением U.
Пусть в момент t=0 замыкается ключ К. Тогда второе уравнение Кирхгофа для выбранного направления обхода контура будет таким:
![]()
 ,
,
или, так как i = C (duC /dt),
![]() ,
(4)
,
(4)
где
![]() −постоянная
времени
RC-цепочки.
−постоянная
времени
RC-цепочки.
Общее решение этого неоднородного уравнения равно сумме его частного решения и общего решения соответствующего однородного. Частное решение легко угадывается: иС частн.=U (оно проверяется простой подстановкой). Тогда
![]()
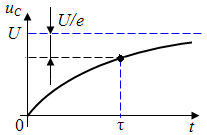 .
.
Коэффициент А определяется из начального условия: иС(+0)=иС(−0)=0. Это даёт: А=−U; и тогда
![]()
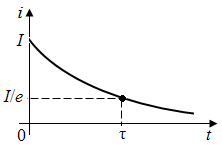 .
.
Ток заряда
 .
.
3.3. Включение постоянного напряжения
в последовательную цепь RL
Процессы при коммутациях в цепи RL описываются такими же дифференциальными уравнениями, как и (2) или (4), поэтому подробнее остановимся лишь на некоторых специфических особенностях.
В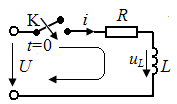 торое
уравнение Кирхгофа:
торое
уравнение Кирхгофа:
![]() ,
или:
,
или:
![]() .
.
Или:
![]() ,
(5)
,
(5)
где
![]() −постоянная
времени цепи
RL.
−постоянная
времени цепи
RL.
Общее решение
неоднородного уравнения (5): i
=
iоднор.+iчастн.=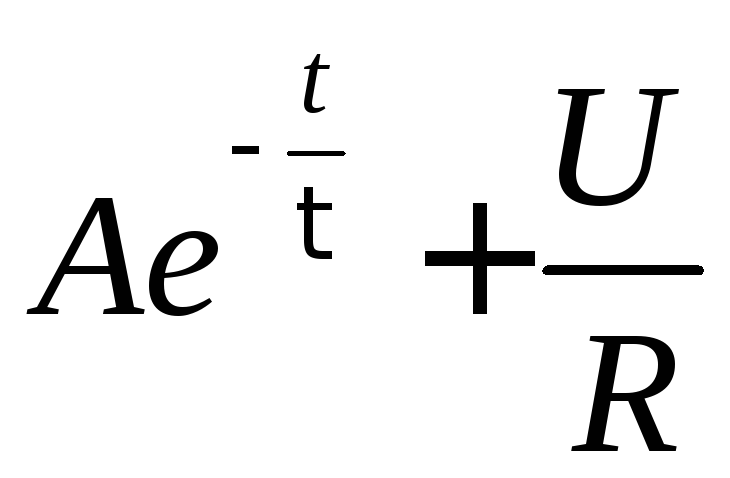 .
.
Н ачальное
условие:i(+0)
= i(−0)=0
(ток через индуктивность скачком
измениться не может, так как это
противоречило бы уравнению (5)). Отсюда
А=−U/R,
и тогда
ачальное
условие:i(+0)
= i(−0)=0
(ток через индуктивность скачком
измениться не может, так как это
противоречило бы уравнению (5)). Отсюда
А=−U/R,
и тогда
 .
(6)
.
(6)
Замечание 1.
При R=0
(подключение напряжения U
к идеальной индуктивности) уравнение
(5) принимает вид:
![]() ,
откуда
,
откуда![]() ,
т.е. ток в катушке линейно и бесконечно
растёт (наклонный пунктир на рисунке).
Это следует и из (6) при разложении
экспоненты в ряд Тейлора по малому
параметру (t/τ):
,
т.е. ток в катушке линейно и бесконечно
растёт (наклонный пунктир на рисунке).
Это следует и из (6) при разложении
экспоненты в ряд Тейлора по малому
параметру (t/τ):
![]() .
.
Замечание 2. Если скачки тока через индуктивности и скачки напряжения на ёмкости запрещены, то скачки напряжения на катушке и тока на конденсаторе не противоречат уравнениям Кирхгофа.
