ChM1

введем числа yi, которые аппроксимируют точное решение Y на данном множестве точек.

Построенную таким образом функцию yi={xi,yi} (i=0,1,…),

называют сеточной функцией.

Далее, заменяем значения производной в уравнении (6.1)

отношением конечных разностей, и осуществляем переход от дифференциальной задачи (6.1), (6.2) относительно функции Y (xi ) к

разностной задаче относительно сеточной функции:

yi 1 F(xi , hi , yi 1, yi ,..., yi k 1),i 1,2,... (6.3) y0 Y0 (6.4).

Разностное уравнение (6.3) записано в общем виде, конкретное выражение его правой части зависит от способа аппроксимации производной. Для каждого численного метода получается свой вид

уравнения (6.3).

На основании анализа вида разностного уравнения можно провести некоторую классификацию численных методов решения задачи Коши

для обыкновенных дифференциальных уравнений.

Если в правой части уравнения (6.3) отсутствует yi 1 , т.е. значение yi 1 , явно вычисляется по k предыдущим значениям yi , yi 1,..., yi k 1 , то

разностная схема называется явной. При этом получается k-шаговый метод: k=1 – одношаговый, k=2 – двухшаговый, т.е. при k=1 для вычисления yi 1 используется лишь одно ранее найденное значение на предыдущем шаге yi .

Если в правой части уравнения (6.3) есть yi 1 – неявная схема, то уравнение (6.3) решают относительно yi 1 с помощью итерационных методов.

Один из самых простых численных методов решения задачи Коши для обыкновенного дифференциального уравнения – это метод Эйлера.

81

Он основан на разложении функции Y(x) в ряд Тейлора, в окрестностях

узлов x=xi (i=0,1,…), в котором отбрасываются все члены, содержащие производные второго и более высоких порядков. Запишем это

yi 1 yi hf (xi , yi ) i 0,1,2,... (6.6). Получение значений искомой функции y(x) заключается в циклическом применении формулы (6.6).

Построенный алгоритм называется методом Эйлера. Разностная схема этого метода представлена соотношениями (6.6). Они имеют вид рекуррентных формул, с помощью которых значения сеточной функции yi+1 в любом узле xi+1 вычисляется по ее значению yi в предыдущем узле xi. В связи с этим метод Эйлера относится к явным одношаговым методам.

Метод Эйлера для систем дифференциальных уравнений имеет

6.3Метод Рунге-Кутта

Этот метод наиболее распространен и основан на вычислении значения функции в четырех точках, что позволяет добиться большой точности.

На каждом шаге вычисления выполняются по формуле:

yi 1 yi h6 (k0 2k1 2k2 k3 ) , где i 0,1,2,... ,

82

k0 f (xi , yi ), k1 f (xi h2 , yi k20 ), k2 f (xi h2 , yi k21 ), k3 f (xi h, yi k2 ). Этот

метод требует большого объема вычислений, но обладает повышенной точностью.

Формула Рунге-Кутта для решения системы дифференциальных уравнений:

Вопросы для самоконтроля:

1.Понятие дифференциального уравнения (геометрический смысл, типы, частное и общее решение).

2.Задача Коши и краевая задача.

3.В какой форме получается приближенное решение дифференциального уравнения по методу Эйлера?

4.Метод Эйлера для решения систем дифференциальных уравнений.

5.Метод Рунге-Кутта.

Лабораторная работа № 6

Задания: Применяя метод Эйлера и метод Рунге-Кутта, решить на отрезке a, b :

1. Дифференциальное уравнение 1-го порядка y' f (x, y) ,

удовлетворяющее начальному условию y(x0 ) y0 (см. таблицу 6.1).

83

84

85

Глава VII

Методы оптимизации

7.1 Постановка задачи. Вводные замечания

Оптимизация – процесс выбора наилучшего варианта из всех возможных. В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения параметров, определяющих данную задачу. Их называют проектными параметрами. Выбор оптимального решения или сравнения двух альтернативных решений проводится с помощью некоторой зависимой величины, определяемой проектными параметрами. Эта величина называется целевой функцией.

Если целевая функция зависит от одного проектного параметра, то мы

имеем одномерную задачу оптимизации.

Цель одномерной оптимизации – определение минимума функции одной переменной, заданной на интервале изменения аргумента. При

этом целевая функция на отрезке должна быть унимодальной, т. е.

на данном отрезке она должна иметь только один минимум.

Когда целевая функция задана в табличном виде, используют различные методы поиска. Они основаны на вычислении целевой функции в отдельных точках и выборе среди них наибольшего или наименьшего значений. Процесс решения задачи состоит в последовательном сужении интервала изменения проектного параметра,

называемого интервалом неопределенности. В начале процесса оптимизации его длина равна b a , а к концу она должна стать менее допустимого значения . Существует ряд алгоритмов решения задачи.

7.1Метод «Золотое сечение»

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Одним из наиболее эффективных методов

86

является метод «золотое сечение». Он состоит в построении последовательности отрезков a1 , b1 , …, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого,

вычисление значения функции производится один раз в точке,

называемой золотым сечением.

Поясним идею метода геометрически. Золотое сечение интервала выбираем так, чтобы отношение длины большего отрезка l1 к длине всего интервала l равнялось отношению длины меньшего отрезка l2 к

длине большего отрезка l1 :

l1 / l l2 / l1 ,

Из этого соотношения можно найти точку деления: l12 l2l l2 (l1 l2 ),

l 2 2 l1l2 l12 0,

(l2 / l1 )2 l2 / l1 1 0,

l2 / l1 ( 1 5) / 2.

Нас интересует только положительное решение, поэтому

l2 / l1 l1 / l ( 1 5) / 2 0.618.

Отсюда

l1 0.618l, l2 0.382l.

Поскольку заранее неизвестно в какой последовательности ( l1 и l2

или l2 и l1 ) делить интервал неопределенности, то рассматриваем внутренние точки, соответствующие этим двум вариантам.

Точки x1 и x2 выбираем с учетом полученных значений частей отрезка. В данном случае:

x1 a0 b0 x2 0.382(b0 a0 ), b0 x1 x2 a0 0.618(b0 a0 ).

87

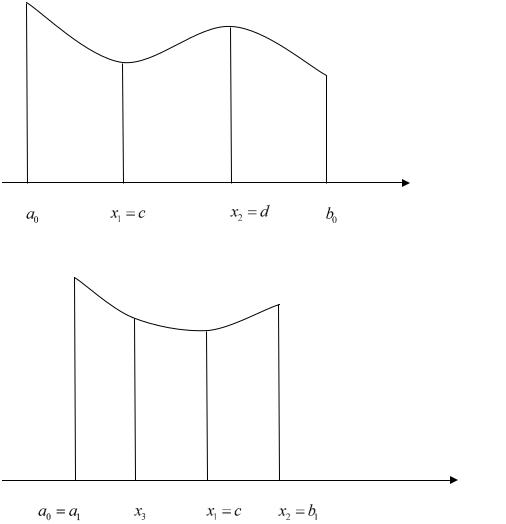
X

Рис. 7.1 Метод «Золотое сечение»

X

Рис. 7.2 Метод «Золотое сечение»

После первого шага мы получили новый интервал неопределенности a0 , x2 . Точка x1 делит этот отрезок в требуемом отношении, т. е.

b1 x1 x2 x1 (b0 a0 ) (x1 a0 ) (b0 x2 )

(b0 a0 ) 0.382(b0 a0 ) 0.382(b0 a0 ) 0.236(b0 a0 ), x2 a0 b1 a1 0.618(b0 a0 ),

b0 a0 (b1 a1 ) / 0.618,

b1 x1 0.236(b1 a1 ) / 0.618 0.382(b1 a1 ).

Вторую точку x3 выбираем на таком же расстоянии от левой границы отрезка, т.е.

x3 a1 0.382(b1 a1 ).

Интервал неопределенности снова уменьшился до величины

88

b2 a2 b1 x3 0.618(b1 a1 ) 0.6182 (b0 a0 ).

Воспользуемся полученными соотношениями, и запишем координаты точек деления c и d на отрезке ak ,bk на k 1 шаге:

c0.618ak 0.382bk ,

d0.382ak 0.618bk .

Длина интервала неопределенности при этом равна:

bk ak 0.618k (b0 a0 ).

Как и в общем случае метода поиска, процесс оптимизации заканчивается при выполнении условия

bk ak .

7.2Многомерная оптимизация

Как правило, в большинстве задач оптимизации, целевая функция зависит не от одного, а от многих проектных параметров.

Метод покоординатного спуска

Пусть требуется найти наименьшее значение целевой функции u=f(x1, x2, …, xn). В качестве начального приближения в n-мерном

направлении убывания функции v от точки M0 до некоторой точки

движение в сторону уменьшения значений функции v.

89