
- •Раздел II. Дифференциальное исчисление функции одной переменной и неопределенный интеграл
- •§ 1Скорость
- •§ 2 Дифференцируемость и производная
- •Непрерывность дифференцируемой функции
- •§ 3 Понятие касательной. Касательная к графику дифференцируемой функции
- •1.Производная степной функции
- •Глава 2. Дифференциал
- •Глава 3. Основные свойства дифференцируемых функций и их применения
- •I. Рскрытие неопределенности вида
- •2.Раскрытие неопределенности вида
I. Рскрытие неопределенности вида
При помощи производных можно находить пределы отношений бесконечно малых функций.
Теорема
1.
Пусть для функций ![]() и
и ![]() выполнены следующие условия6
выполнены следующие условия6
а)
они определены и дифференцируемы в
некоторой окрестности точки ![]() ,
за исключением, быть может самой точки
,
за исключением, быть может самой точки
![]() ,
причем
,
причем ![]() и
и ![]() в указанной окрестности;
в указанной окрестности;
б)![]() и
и ![]() при
при ![]() ;
;
в) существует предел отношения производных
![]()
Тогда существует равный ему предел отношения данных функций:
![]()
Доказательство.
Доопределим функции ![]() и
и ![]() в точке
в точке ![]() ,
положив
,
положив ![]() и
и ![]() .
Тогда в указанной окрестности функции
будут непрерывны. Для любого
.
Тогда в указанной окрестности функции
будут непрерывны. Для любого ![]() из этой окрестности на отрезке между
из этой окрестности на отрезке между
![]() и
и ![]() выполнены условия теоремы Коши.
выполнены условия теоремы Коши.
Поэтому
![]() ,
где C
некоторая точка между
,
где C
некоторая точка между ![]() и
и ![]() .
Так как при
.
Так как при ![]() ,
,
![]() ,
то
,
то ![]()
Теорема доказана.
Пример.
![]() .
.
Замечание.
1) Правило Лопиталя справедливо и при
![]() .
.
Если производные
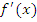 и
и 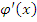 удовлетворяют тем же требованиям, что
и сами функции
удовлетворяют тем же требованиям, что
и сами функции  и
и 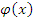 ,
то правило Лопиталя можно применять
повторно, а при соответствующих условиях
и несколько раз, т.е.
,
то правило Лопиталя можно применять
повторно, а при соответствующих условиях
и несколько раз, т.е.
![]()
Пример.
![]()
Здесь правило Лопиталя было применено три раза.
Правило Лопиталя переносится на тот случай, когда аргумент
 стремится к бесконечности. Действительно,
произведем замену переменной (аргумента)
стремится к бесконечности. Действительно,
произведем замену переменной (аргумента)
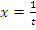 .
Тогда
.
Тогда  при
при 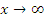 .
Поэтому
.
Поэтому 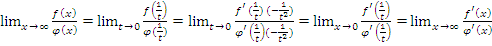 .
.Если предел отношения
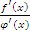 не существует, то отсюда еще не следует,
что не существует предел отношения
самих функций
не существует, то отсюда еще не следует,
что не существует предел отношения
самих функций 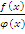 .
Правило Лопиталя в этом случае
неприменимо.
.
Правило Лопиталя в этом случае
неприменимо.
Пример.
Если ![]() ,
то
,
то ![]() и предел в точке не существует.
и предел в точке не существует.
Но
![]() .
.
2.Раскрытие неопределенности вида
Правило Лопиталя применимо и к отношению бесконечно больших функций.
Теорема
2.
Пусть для функций ![]() и
и ![]() выполнены следующие условия:
выполнены следующие условия:
а)
они определены и дифференцируемы в
некоторой окрестности точки ![]() ,
за исключением самой точки
,
за исключением самой точки ![]() ,
причем
,
причем ![]() и
и ![]() в указанной окрестности;
в указанной окрестности;
б)![]() и
и ![]() при
при ![]() ;
;
в) существует предел отношения производных
![]()
Тогда существует равный ему предел отношения данных функций:
![]()
Доказательство.
Если в указанной окрестности точки ![]() по одну сторону от
по одну сторону от ![]() выбрать точки
выбрать точки ![]() и
и ![]() ,
то на отрезке между
,
то на отрезке между ![]() и
и ![]() выполнены условия теоремы Коши.
выполнены условия теоремы Коши.
Поэтому
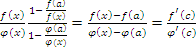 , где C
некоторая точка между
, где C
некоторая точка между ![]() и
и ![]() .
Отсюда
.
Отсюда
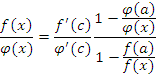
Зададим
любое ![]() и найдем такое
и найдем такое ![]() ,
что
,
что
![]()
По
условию теоремы точку ![]() можно выбрать и зафиксировать так ,
чтобы для любой точки
можно выбрать и зафиксировать так ,
чтобы для любой точки ![]() между
между ![]() и
и ![]() было
было
![]()
Так
как ![]() и
и ![]() при
при ![]() ,
то
,
то
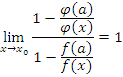
Поэтому
существует ![]() такое, что при
такое, что при ![]() будет
будет

Но тогда при указанных аргументах
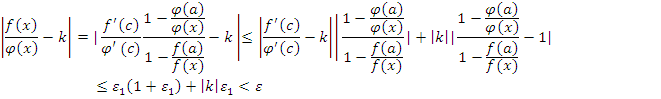
По
определению предела это означает, что
![]() .
.
Теорема доказана.
Замечания, сделанные по теореме 1, относятся и к теореме 2.
Пример.
![]() .
.
При
помощи правила Лопиталя могут раскрываться
и неопределенности отличные от ![]() и
и ![]() ,
так, например, неопределенности вида:
,
так, например, неопределенности вида:
![]() ;
;
![]() ;
;
![]() и
и ![]() путем преобразований сводятся к отношению
бесконечно малых или бесконечно больших
функций.
путем преобразований сводятся к отношению
бесконечно малых или бесконечно больших
функций.
Пример
1.
![]() .
.
Здесь
мы имеем неопределенность вида ![]() (произведение бесконечно малой и
бесконечно большой функций).
(произведение бесконечно малой и
бесконечно большой функций).
Пример
2.
![]()
Здесь
мы имели неопределенность вида ![]() (разность двух бесконечно больших
функций одного знака).
(разность двух бесконечно больших
функций одного знака).
Пример
3. ![]() .
.
Здесь
мы имеем неопределенность вида ![]() (показательно – степенная функция с
бесконечно малыми основанием и показателем
степени).
(показательно – степенная функция с
бесконечно малыми основанием и показателем
степени).
Аналогично
раскрываются неопределенности вида
![]() и
и ![]() .
.
Асимптоты
Определение
1.
Прямая ![]() называется вертикальной асимптотой
графика функции
называется вертикальной асимптотой
графика функции ![]() ,
если при
,
если при ![]() или
или ![]()
![]() бесконечно большая.
бесконечно большая.
Например,
график функции ![]() имеет вертикальную асимптоту
имеет вертикальную асимптоту ![]() ,
т.к.
,
т.к.
![]()
Пусть
функция ![]() определена на промежутке
определена на промежутке ![]() или
или ![]() .
.
Определение
2.
Прямая ![]() называется наклонной асимптотой графика
функции
называется наклонной асимптотой графика
функции ![]() при
при ![]() ,
если функция
,
если функция ![]() представима в виде
представима в виде ![]() ,
где
,
где ![]() бесконечно малая функция при
бесконечно малая функция при ![]() .
.
Теорема.
Для того чтобы график функции ![]() имел при
имел при ![]() наклонную асимптоту
наклонную асимптоту ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
![]()
Доказательство.
Необходимость.
Пусть график функции ![]() имеет при
имеет при ![]() асимптоту
асимптоту ![]() ,
т.е. выполняется равенство
,
т.е. выполняется равенство
![]() .
.
Но
тогда ![]() и
и ![]()
Достаточность.
Пусть для ![]() справедливы равенства
справедливы равенства
![]()
Тогда
из второго равенства следует, что ![]() ,
где
,
где ![]() бесконечно малая функция при
бесконечно малая функция при ![]() .
Но тогда
.
Но тогда ![]() ,
и, следовательно, прямая
,
и, следовательно, прямая
![]() является наклонной асимптотой графика
функции
является наклонной асимптотой графика
функции ![]() .
.
Пример.
Найти асимптоты графика ![]() .
.
Так
как ![]() ,
то прямая
,
то прямая ![]() является вертикальной асимптотой.
является вертикальной асимптотой.
Далее,
![]() .
.
Следовательно,
наклонной асимптотой будет прямая ![]() .
.
Исследование функций. Построение графика
В заключение приведем схему общего исследования функции.
Найти область определения функции.
Исследовать непрерывность функции и найти ее точки разрыва.
Найти асимптоты графика.
Выяснить является ли данная функция четной или нечетной.
Выяснить является ли данная функция периодической.
Исследовать возрастание и убывание функции; найти точки экстремума.
исследовать направление выпуклости графика и найти точки перегиба.
Найти точки пересечения графика с осями координат и исследовать поведение функции при
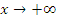 и
и 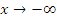 .
.
Данные исследования следует записать в таблицу и использовать при построении графика функции.
В
качестве примера проведем полное
исследование функции ![]() и построим ее график.
и построим ее график.
Область определения функции
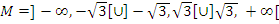 .
.Функция является непрерывной как частное двух непрерывных функций.
Так как
 ,
то прямые
,
то прямые 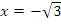 и
и 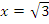 являются вертикальными асимптотами
графика. Далее имеем
являются вертикальными асимптотами
графика. Далее имеем 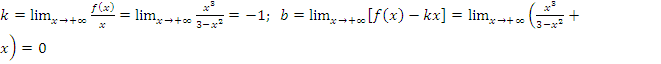 .
Следовательно,
прямая
.
Следовательно,
прямая 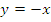 есть наклонная асимптота графика.
есть наклонная асимптота графика.Так как
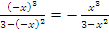 ,
то данная функция является нечетной,
поэтому ее график симметричен относительно
начала координат.
,
то данная функция является нечетной,
поэтому ее график симметричен относительно
начала координат.Функция не периодическая.
Функция
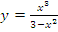 дифференцируема всюду в области ее
определения. Производная функции
дифференцируема всюду в области ее
определения. Производная функции
![]()
![]() в точках
в точках ![]() ,
,
![]() ,
,
![]() .
.
![]() при
при ![]() ,
т.е. на множестве
,
т.е. на множестве ![]() .
.
![]() при
при ![]() ,
т.е. на множестве
,
т.е. на множестве ![]() .
.
Отсюда
следует, что функция возрастает на
множестве
![]()
и
убывает на множестве ![]() .
.
Производная
меняет знак в точках ![]() и
и ![]() . Это точки экстремума. Так как в точке
. Это точки экстремума. Так как в точке
![]() знак производной меняется с – на + (при
возрастании аргумента), то в этой точке
функция имеет минимум
знак производной меняется с – на + (при
возрастании аргумента), то в этой точке
функция имеет минимум ![]() .
.
Так
как в точке ![]() знак производной меняется с + на -, то в
этой точке функция имеет максимум
знак производной меняется с + на -, то в
этой точке функция имеет максимум ![]() .
.
В
точке ![]() функция экстремума не имеет, т.к. в этой
точке производная не меняет своего
знака.
функция экстремума не имеет, т.к. в этой
точке производная не меняет своего
знака.
Вторая производная функции
![]() ;
;
![]() в точке
в точке ![]() .
Далее,
.
Далее, ![]() на множестве
на множестве ![]() ,
поэтому на этом множестве график функции
направлен выпуклостью вверх:
,
поэтому на этом множестве график функции
направлен выпуклостью вверх: ![]() на множестве
на множестве ![]() ,
значит на этом множестве график направлен
выпуклостью вниз.
,
значит на этом множестве график направлен
выпуклостью вниз.
В
точке ![]() вторая производная меняет свой знак с
- на +, следовательно, точка
вторая производная меняет свой знак с
- на +, следовательно, точка ![]() является точкой перегиба графика.
является точкой перегиба графика.
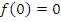 , т.е. график функции проходит через
начало координат.
, т.е. график функции проходит через
начало координат.
![]()
Результаты исследования представим таблицей
|
|
|
-3 |
- |
0 |
|
3 |
|
|
|
|
4,5 минимум |
не сущ. |
0 перегиб |
не сущ. |
-4,5 максимум |
|
|
|
-
|
0 |
не сущ. |
0 |
не сущ. |
0 |
- |
|
|
+ + выпуклость вниз |
не сущ. |
0 |
не сущ. |
- - выпуклость вверх | ||
