1.Производная степной функции
Пусть
,
где 
- любое вещественное число. Тогда для
любого 
.
Так
как 
,
то при 
,
т.е. 
.
В
частности , 
.
Зная производную степенной функции и правила дифференцирования сумм, произведений и частных, можно дифференцировать целые и дробно – рациональные функции. Например,
2. Производная показательной функции
Пусть
,
где 
и 
.
Тогда для любого
:
.
Так
как 
,
то при 
, то есть 
.
В
частности, 
.
3. Производная логарифмической функции
Пусть
,
где 
и
.
Тогда для любого 
:
Так
как 
,
то при 
то есть 
.
В
частности, 
.
Заметим, что производную логарифмической функции можно получить как производную функции, обратной показательной:
.
4. Производные тригонометрических функций
Пусть
. Тогда для любого
:
.
Так
как 
,
то при 
благодаря непрерывности 
,
,
т.е. 
.
Аналогично
доказывается, что 
.
Пусть
.
Тогда для любого 
:
.
Аналогично
доказывается, что для любого 
:
5. Производные обратных тригонометрических функций
Пусть
. Тогда для любого
по правилу дифференцирования обратной
функции:
.
Так
как 
, то 
.
Пусть
.
Тогда для любого 
:
Так
как 
, то 
.
Полученные результаты можно представить в виде таблицы производных основных элементарных функций .
;
;
;
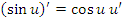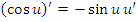В
заключение рассмотрим показательно –
степенную функцию 
,
где 
и функции 
имеют производные в точке 
.
Воспользуемся так называемым методом
логарифмического дифференцирования.
Рассмотрим сначала функцию 
.
Она дифференцируема, причем 
.
Так как 
,
то данная функция также дифференцируема,
причем 
,
то есть 
.
Например,
.
Производные высших порядков
Если
функция 
в каждой точке некоторого промежутка
имеет производную, то эта производная
является новой функцией на данном
промежутке. Возможно, что функция 
имеет производную. Эту производную
называют второй производной от функции
и обозначают 
или 
.
Таким образом, по определению
По индукции производная n–го порядка определяется как производная от производной (n-1) -го порядка и записывается:
При
этом предполагается, что производная
(n-1)
-го порядка 
определена во всех точках некоторой
окрестности 
и имеет производную в самой точке 
.
Для некоторых элементарных функций можно указать формулу производной n –го порядка, справедливость которой проверяется методом математической индукции.
Например,
для функции 
имеем 
.
Действительно, это верно для n=1
. Предположим, что это верно для n=k
и проверим справедливость для n=k+1
. Имеем 
.
В
частности,
.
Для
функции 
имеем 
.
Действительно,
это видно для n=1:
. Предположим, что это верно для n=k+1:
Аналогично,
.
Для отыскания производной n-го порядка от произведения функций, имеющих производные до порядка n в данной точке, весьма полезной является формула Лейбница:
Докажем
ее методом математической индукции.
Для n=1
она имеет вид 
и потому справедлива. Предположим, что
она верна для n=k
и докажем ее справедливость для n=k+1
.
Так
как 
и 
, то окончательно имеем
Например,
если 
,
то 
,
так
как 
для n>2
.
Механический смысл второй производной
Пусть
закон движения материальной точки по
некоторой прямой линии имеет вид 
.
Как известно, первая производная 
функции 
дает зависимость мгновенной скорости
движущейся точки от времени 
.
По определению второй производной 
, а 
есть скорость изменения 
в момент 
.
Как известно из механики, последняя
величина является ускорением 
в момент 
.
Итак, вторая производная 
есть ускорение:
Например,
если 
(
-
постоянное ускорение свободного
падения), то 
,а
ускорение 
.
Параметризованные пути
Пусть
каждой точке 
некоторого промежутка
поставлена в соответствие точка
плоскости 
,то есть задано отображение 
.
Это отображение задается при помощи
двух вещественных функций : 
и y
. Отображение 
называется непрерывным или дифференцируемым,
или непрерывно – дифференцируемым,
если функция 
и 
соответственно непрерывны, имеют
производные или имеют непрерывные
производные.
Определение
1.
Непрерывное 
отображение называется параметризованным
(плоским) путем; переменная 
- параметром, образ 
- носителем параметризованного пути.
Если промежуток замкнут 
, то 
- замкнутый параметризованный путь, а
точки 
и 
называются началом и концом этого пути.
У
различных параметризованных путей
может быть один и тот же носитель. В этом
случае говорят о различных параметризациях
носителя. Например, множество точек
{
}
(верхняя единичная полуокружность)
является носителем следующих двух
параметризованных путей
Для
различных параметризаций одного и того
же носителя вводится понятие эквивалентности
следующим образом. Функцию, отображающую
один промежуток на другой, называют
преобразованием параметра, если она
непрерывна и монотонно возрастает. Два
параметризованных пути 
и 
называются эквивалентными, если
существует цепочка параметризованных
путей 
,
что 
и для любых двух соседних путей 
и 
существует преобразование параметра
или 
, что 
или 
.
Например,
две указанные параметризации полуокружности
эквивалентны, так как можно указать
соответствующее преобразование параметра
: 
.
Определение
2.
Все эквивалентные параметризованные
пути объединяются в один класс 
,
который называется путь.
Выделим некоторые специальные виды путей.
Путь
называется простым (или кривой Жордана),
если он замкнут и существует такая его
параметризация 
, которая на 
взаимно однозначна.Замкнутый путь
называется замкнутым контуром, если
его конец совпадает с его началом.Замкнутый путь
называется простым замкнутым контуром
(контуром Жордано), если он является
замкнутым контуром и существует такая
его параметризация 
, которая на 
взаимно однозначна.Путь
называется гладким, если существует
его такая непрерывно дифференцируемая
параметризация 
, что для любой точки 
производные 
и 
одновременно не равны нулю.
Естественным образом вводится понятие кусочно гладкого пути.
Например,
верхняя полуокружность является примером
кривой Жордана, а окружность – простым
замкнутым контуром (контуром Жордано).
Более того, это гладкие Жордановы кривая
и контур. Для доказательства этого
утверждения достаточно рассмотреть
параметризацию 
, где 
для полуокружности и 
для всей окружности.
Параметрические заданные функции и их дифференцирование
Пусть
задан параметризованный путь 
при помощи функций 
, . Пусть первая из этих функций 
взаимно однозначно отображает 
на некоторый промежуток 
, т.е. существует обратная функция 
, отображающая 
на 
.
В этом случае 
является функцией от 
, определенной композицией: 
. О такой функции говорят, что она задана
параметрическими равенствами
Если
функции 
и 
имеют производные в некоторой точке
, причем 
, то можно через эти производные выразить
производную 
как функции от 
(обозначается 
)
. Действительно, используя правила
дифференцирования сложных и обратных
функций, получаем
Например,
если 
, 
,
то
и
производная определяется без использования
явного выражения 
через 
.
Если
функция 
и 
имеют вторые производные, то через них
можно выразить вторую производную 
как функции от 
(обозначается 
).
При выводе формулы используется найденное
выше правило, но применяется оно не к
как функции от 
, а к 
как функции от 
:
Аналогичные формулы можно получить для производных третьего и более высокого порядка.
Касательная к кривой Жордана
Рассмотрим кривую Жордана с параметрическими уравнениями
Пусть
в окрестности значения параметра 
является функцией от 
и 
. Тогда для 
из этой окрестности часть кривой Жордана
есть график дифференцируемой функции,
а угловой коэффициент касательной к
этой кривой в точке 
(
,
)
равен
Поэтому
уравнение касательной в точке со
значением параметра 
имеет вид
Аналогично,
если в окрестности значения параметра
является функцией от 
и 
,то уравнение касательной к кривой
Жордана в точке 
имеет вид:
Оба
случая приводят к следующей симметричной
форме записи уравнения касательной 
.
Например, для полуокружности
уравнение
касательной в точке с параметром 
:
или 