Непрерывность дифференцируемой функции

Установим связь между свойствами непрерывности и дифференцируемости функции в данной точке .

Теорема. Если функция в данной точке дифференцируема, то она в этой точке непрерывна.

Доказательство. Пусть функция дифференцируема в точке . Тогда ее приращение представимо в виде

.

Но тогда при будет , а это означает непрерывность функции в точке .

Итак, непрерывность в данной точке является необходимым условием для дифференцируемости. Однако достаточным условием она не является. Действительно, рассмотрим в качестве примера функцию в точке . Для нее

и предела в точке нет, а потому нет производной и нет дифференцируемости, но , что означает непрерывность.

Укажем еще один пример функции

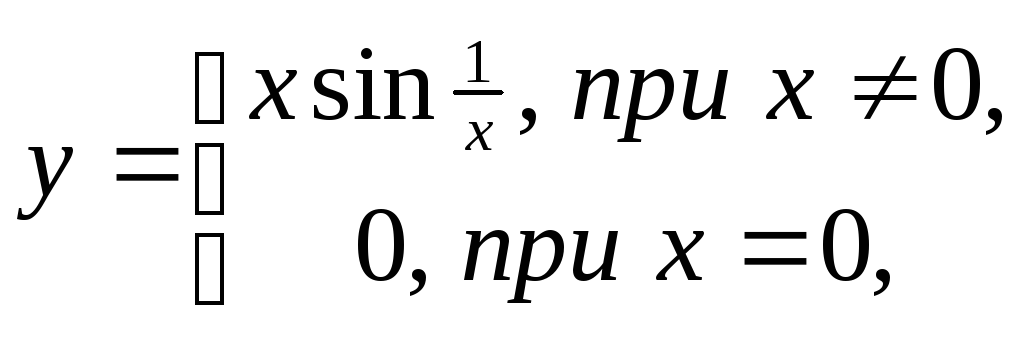
которая в точке непрерывна (так как), но не дифференцируема (так как не имеет предела в точке ).

§ 3 Понятие касательной. Касательная к графику дифференцируемой функции

Из предыдущих разделов математики студентам известны различные плоские кривые (например, кривые второго порядка: окружности, эллипсы, гиперболы, параболы, а также графики различных непрерывных функций). Важным является понятие касательной прямой к таким кривым. Приведем описание этого понятия.

Пусть L одна из таких плоских кривых и А – точка на L. Если B – другая точка на L, то прямая P, проходящая через A и B, называется секущей для L. Пусть точка B движется по L, приближаясь к А сколь угодно близко. Тогда секущая будет вращаться вокруг точки А. Если при этом существует, проходящая через А, прямая Т такая, что угол между Р и Т будет сколь угодно мал (т.е. Р будет стремится к положению Т), то прямая Т называется касательной к L в точке А. Касательная существует не всегда. Так, у графика функции в точке касательной нет.

Действительно (см. рис.2), график состоит из двух полупрямых и , образующих угол с вершиной в начале координат. При секущая проходит вдоль , а при – вдоль , поэтому общего предельного положения секущих нет. График в точке имеет и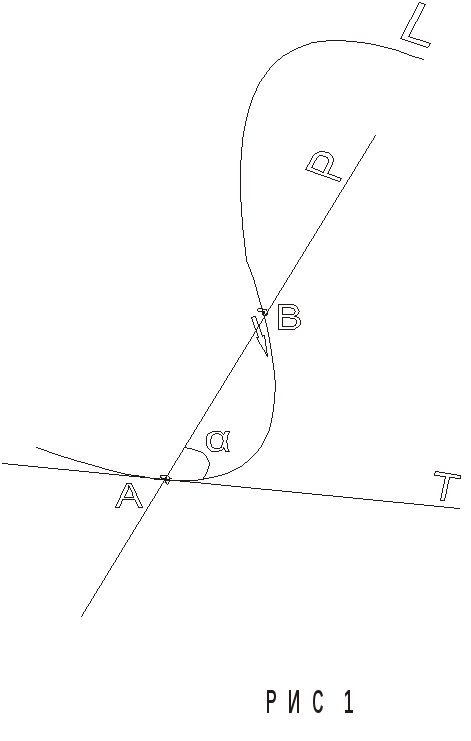злом.

Пусть теперь L это график функции , заданной на промежутке и дифференцируемой в некоторой внутренней точке этого промежутка.

Пусть , где , соответствующая точка графика (см. рис.3). Если другая точка графика, то и и секущая Р, проходящая через А и В, наклонена к оси Ох под углом .

Проведем через А прямую Т, образующую с осью Ох угол равный . Угол между Р и Т равен . Когда В приближается к А сколь угодно близко, то и, благодаря этому с учетом непрерывности функции :

,

то есть . Следовательно, Т является касательной к графику в точке А. Угловым коэффициентом касательной Т является производная функции в точке .

Итак, график дифференцируемой функции в соответствующей точке имеет касательную, угловой коэффициент которой равен производной в данной точке. В этом заключается геометрический смысл производной.

Видно и обратное, если график функции в данной точке А имеет касательную, не перпендикулярную оси Ох, то в данной точке существует при предел (благодаря непрерывности ), функция в данной точке дифференцируема. Ясно, что в точках разрыва касательной быть не может. В точках же, где нет дифференцируемости, касательная к графику может быть, но перпендикулярная оси Ох (см. рис 4). Значение углового коэффициента касательной к графику функции позволяет составить уравнение этой касательной. Известно, что всякая прямая (не перпендикулярная оси Ох), проходящая через точку А(), имеет уравнение .

Так как для касательной , то уравнение касательной .

Прямая, проходящая через А() и перпендикулярная касательной, называется нормалью к графику функции . Так как ее угловой коэффициент , то уравнение нормали имеет вид .

Например, для кривой в точке имеет , поэтому уравнение касательной в точке А()

,

а уравнение нормали .

Дифференцирование суммы, произведение и частного

ТЕОРЕМА. Если функции и имеют производные в данной точке , то в этой точке имеют производные их сумма, разность, произведение и частного (последнее при условии ), причем имеют место формулы:

;

Доказательство. 1. Обозначим . Тогда .

Отсюда (при ) .

При правая часть этого равенства имеет предел, равный , поэтому и левая часть имеет тот же предел, то есть

.

2. Обозначим .

Тогда =.

Отсюда.

Функция благодаря дифференцируемости в точке непрерывна в этой точке и потому при . Следовательно, существует предел . При этом .

3. Обозначим . Заметим, что из условия и непрерывности в точке следует, что в некоторой окрестности .

Имеем .

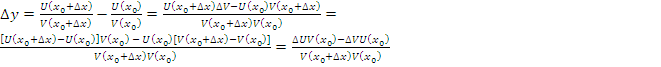Отсюда , поэтому существует предел этого выражения при

.

Теорема доказана.

Отметим два важных следствия.

Следствие 1. Если С – постоянная, а дифференцируема в данной точке, то в этой точке дифференцируема , причем , то есть постоянный множитель выносится за знак производной.

Действительно, , а производная постоянная функции равна нулю:

.

Следствие 2. Если дифференцируема в данной точке, то в этой точке дифференцируема любая натуральная степень , причем

.

Действительно, это справедливо для и . Общий случай доказывается методом математической индукции.

Пусть утверждение верно для . Тогда

.

Дифференцирование сложной функции

ТЕОРЕМА. Пусть функция имеет производную в точке , а функция имеет производную в точке . Тогда сложная функция (композиция) имеет производную в точке , причем справедлива формула

.

Доказательство. Приращению аргумента соответствует приращение функции . Приращению в свою очередь соответствует приращение функции . Так как дифференцируема в точке , то

,

где при.

Отсюда .

При благодаря непрерывности в точке имеем и . Поэтому имеет предел при , и этот предел равен:

.

Дифференцирование обратной функции

ТЕОРЕМА. Пусть у функции , отображающей промежуток в промежуток , имеется обратная функция . Пусть для соответствующая точка . Если имеет производную в точке , отличную от нуля , то обратная функция имеет производную в точке , причем

.

Доказательство. Придадим аргументу обратной функции в точке приращение . Этому приращению соответствует приращение также отличное от нуля, благодаря взаимно однозначному соответствию между и . Очевидно,

;

если , то, согласно непрерывности в точке , будет . По условию , поэтому существует предел , то есть обратная функция имеет производную, причем

.

Производные основных элементарных функций

Покажем, что все основные элементарные функции дифференцируемы в любой внутренней точке их областей определения и найдем их производные. При этом используем различные замечательные пределы.