Методы и средства передачи информации (Лекция №9)

а сгруппировав члены с учетом независимости производных по времени и по координатам, получим:

Учитывая, что вектор А недоопределен, можно положить, что

так как rot rot А при этом не меняется. Это действие называется калибровкой векторного потенциала. Этот вариант калибровки называется калибровкой Лоренца и удобен при расчете переменных полей. С учетом (2.26) уравнение (2.25) примет вид:

Вообще говоря, полученного уравнения достаточно для достижения поставленной цели, а именно, для установления связи между векторным потенциалом и источником поля − сторонним током проводимости. Однако более простой вид связи между вектором А и током J следует из анализа уравнения (9.27). Для этого проведем дополнительные действия.

Одновременно, с учетом представления div grad ϕ = 2 ϕ и принятого вы-

ражения калибровки (9.26) из уравнения (9.24), поменяв местами порядок дифференцирования, для скалярного потенциала получим соотношение:

из которого следует уравнение для скалярного потенциала:

11

х, у, z удовлетворяют уравнению одного и того же типа − уравнению Даламбера:

Уравнение (9.29) относится к уравнению гиперболического типа и называется волновым. Решением уравнения (9.29) являются функции бегущей волны. Это проще всего можно показать для однородного волнового уравнения:

Это уравнение является частным случаем уравнения Даламбера для области пространства свободной от сторонних источников поля.

Ограничимся рассмотрением на примере функции прямоугольной декартовой системы координат Ф( x , y , z ,t )= Ф( z ,t ). При этом уравнение (9.30) при-

мет вид одномерного однородного уравнения в частных производных

решением которого (что легко проверить подстановкой этого решения в уравнение) имеет вид:

где Φ1 и Φ 2 – функции бегущих плоских (т.е., с плоским фронтом) волн, у кото-

зовой скоростью v вдоль оси z, а Φ 2 – в обратном направлении. Заметим, что аналогично записываются прямые и отраженные (обратные) волны в длинной линии.

В отсутствии направляющей структуры в свободном пространстве в сферической системе координат для полей точечного источника (в пространстве вне

12

источника) волновое уравнение (9.30) с учетом коэффициентов криволинейности осей имеет вид:

откуда с обратной заменой переменных получим решение уравнения (9.32) в ви-

окружающем заряд пространстве переходит в уравнение Лапласа 2 ϕ = ∆ϕ = 0

( ∆ – символ скалярного лапласиана) для потенциала ϕ( r ) (в силу центральной

симметрии зависящего только от расстояния r до точки наблюдения) электростатического поля Е, которое в сферической системе координат имеет вид:

13

Решение уравнения (9.33), полагая радиус r величиной конечной, сводится

кинтегрированию уравнения

∂r 2 ∂ϕ = 0.

∂r ∂r

лучают из известных значений искомой функции. Такие данные в теории поля называют граничными условиями. Это могут быть данные о значениях поля (или потенциала) в точках или на поверхностях анализируемой области пространства, например в бесконечно удаленных точках. Так как в нашем случае постоянных интегрирования две, то для составления двух уравнений необходимо иметь данные как минимум в двух точках анализируемого пространства, либо данные о функции и её производной в одной точке. В нашем случае можно ука-

зать только одно известное значение ϕ( r ) = 0 при r → ∞ (стремящемся к беско-

нечности), полагая физическое поле бесконечно удаленного источника убывающим. При этом C 2 = 0. Для определения постоянной C 1 прямых данных нет.

Поэтому воспользуемся косвенными данными.

Рассмотрим решение задачи исходя из теоремы Гаусса. Как мы знаем (см. лекцию №8), электростатическое поле точечного источника в свободном про-

Теперь, зная, что решение волнового уравнения выражается в функции бегущих волн, если предположить, что при фазовой скорости v ≠ ∞,

14

то при v →∞, выражение (9.35) перейдет в (9.34), то есть решение (9.34) явля-

ется предельным переходом для более общего решения (9.35).

Заметим, что мы лишь показали, какой вид функции логично ожидать.

Из найденного выражения (9.35) для потенциала точечного источника с применением метода суперпозиции следует решение для потенциала в точке наблюдения М от распределенного в объеме V заряда ρ( x , y , z ,t ) :

Из выражения (9.36) следует, что в точке наблюдения M в момент времени t суммируются парциальные потенциалы от значений ρk(t,r), взятых в разные моменты времени t'= t – r'/v, что иллюстрирует рис. 9.3. Этот факт характеризует понятие «запаздывающие потенциалы».

ρ2

Рисунок 9.3 − Иллюстрация к понятию «запаздывающие потенциалы Аналогично, рассмотрев выражение для векторного потенциала А элемента

постоянного тока Il (закон Био-Савара – см. лекцию №8, c. 17) и формально перейдя от уравнения Пуассона для векторного потенциала постоянного элемента тока Il

к уравнению Даламбера, можно записать для векторного потенциала выражение

15

статического ( ∂/ ∂t →0 и J = 0) и стационарного ( ∂/ ∂t →0 и J ≠ 0) полей, потен-

циалы электромагнитного поля называют «запаздывающими» – т. е. учитывающими время распространения волны.

С точки зрения вопроса определения структуры магнитного поля, который мы анализируем, понятия «запаздывающие потенциалы», возникшее, что называется, попутно не имеет прямого отношения. Однако с мировоззренческой точки зрения, полученный результат весьма важен, так как подтверждает уже известное нам понятие эффекта «близкодействия» с которым мы познакомились при рассмотрении распространения волн в длинной линии.

Возвращаясь к рассматриваемому вопросу, запишем формулы (9.36) и (9.38) для линейных зарядов τ( r ,t ) и токов i(r, t), характеризующих решения за-

дач в двухпроводной линии. При этом формулы (9.36) и (9.38) принимают вид:

Заметим, что в отличие от скалярного выражения (9.39), выражение (9.40) соответствует векторной функции, поэтому распадается на три скалярных уравнения

по координатным осям ξk. Но так как в двухпроводной линии ток совпадает пусть с осью z, то выражение для векторного потенциала ограничится только од-

ной координатной осью z, т.е. A = z 0 A z , где z 0 − орт продольной оси линии.

Выражение (9.39) окажется полезным при рассмотрении в дальнейшем изложении понятия перестановочной двойственности, применяемого для расчета

16

первичных параметров двусвязных систем. Выражение (9.41) является основой получения силовых линий магнитного поля в двусвязных структурах.

Объясняется это тем, что каждый из токов в проводниках двухпроводной линии обуславливает векторный потенциал, параллельный линиям тока и имеющий единственную продольную составляющую, например по оси z, не зависящую от координаты z. Очевидно, что результирующий векторный потенциал А=z0 Аz(х, у) будет равен алгебраической сумме векторных потенциалов отдельных токов, а результирующая магнитная индукция В =rotА определится дифференцированием:

Теперь запишем через векторный потенциал А уравнение линий магнитной индукции В. Для этого сначала запишем дифференциальное уравнение линий магнитной индукции, которое следует из определения вектора индукции поля как касательной к силовой линии (см. рис. 9.4).

В

r0

Рисунок 9.4 − К выводу уравнения силовой линии

Здесь вектор r 0 = x 0 dx + y 0 dy + z 0 dz , а вектор B = x 0 B x + y 0 B y + z 0 B z , а

условие колинеарности этих векторов выразится равенством векторного произ-

ведения [r 0 ,B ]= 0, которое в явном виде с учетом равенстваH z = 0 и плоскопа-

раллельной структуры поля запишется как

17

Если теперь в дифференциальном уравнении (9.42) этих линий сделать подстановку из уравнения (9.41), то получим

Adxz dx + Adyz

Откуда Аz(х, у) = const и есть искомое уравнение силовой линии.

Теперь необходимо установить вид этой силовой линии, т.е. вид кривой Аz(х, у) = const в двухпроводной линии.

В общем случае на поверхности проводов Аz(х, у) ≠ const, так как магнит-

ные линии пересекают эту поверхность.

Ограничимся рассмотрением магнитных силовых линий вне проводов двухпроводной линии. Найдем вид функции Аz(х, у).

Исходим из того, что по закону полного тока на расстоянии r ≥ a , где а −

радиус провода, напряженность магнитного поля H α = 2 Iπr , а магнитная ин-

Для двух проводов векторные потенциал получим в виде суммы вкладов от каждого из проводов. При этом аналогично рассмотрению задачи для электростатического поля двухпроводной линии обозначим расстояния от «положитель-

18

ного» тока r + . Пусть это ток «уходящий за плоскость листа», соответствующий положительно заряженной оси (т.е. провод, к которому приложен положительный зажим источника напряжения). Расстояния от «отрицательного» тока (или обратного провода линии) r − . Тогда Суммарный векторный потенциал

Формула (9.44 повторяет по структуре выражение скалярного потенциала

электростатического поля двухпроводной линии. Также как и в случае скалярно-

по записи эквипотенциальные кривые электростатического поля, имеющие вид

Этим доказано, что силовые линии магнитного поля двухпроводной линии

представляют собой окружности, центры которых определены аналогично центрам эквипотенциальных окружностей электростатического поля в плоскости поперечного сечения двухпроводной линии.

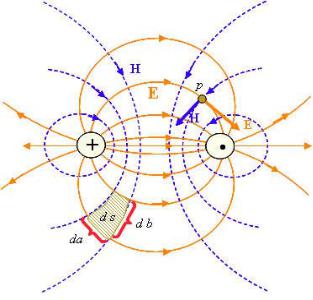
В итоге можно заключить, что линии электрического поля, если пренеб-

речь падением напряжения на проводах, в поперечном сечении линии также образуют окружности, нормальные к линиям магнитного поля. Картина поля пока-

зана на рис. 9.5. Заметим, что падение напряжения на проводах (за счет погон-

ного сопротивления R =1/σS ) приводит к изменению (уменьшению в направлении от генератора к нагрузке) напряжения в поперечных сечениях линии (это явление называют потерями напряжения). Это искажает напряженность электриче-

19

ского поля в линии за счет появления ненулевой тангенциальной его составляющей (поле теоретически не идеально плоскопараллельное). Однако тангенциальная составляющая электрического поля обычно ничтожно мала по

сравнению с нормальной составляющей. Так, если плотность тока в проводе J

= 1 А/мм², то падение напряжения на одном сантиметре медного провода

на поверхности провода при таком значении плотности постоянного тока (определяемой приложенным к линии напряжении) составляет примерно 1 В/см и выше.

Рисунок 9.5 – Структура полей в двухпроводной линии

Исходя из плоскопараллельной модели поля в такой линии, найдем выра-

жение для мощности, передаваемой через её поперечное сечение. Для этого за-

пишем поток вектора Пойнтинга через дуговые четырехугольники, образован-

ные в плоскости поперечного сечения пересечением силовых линий электрического и магнитного полей (рис. 9.3). Углы при вершинах этих четырехугольни-

ков прямые (так как это углы между силовыми линиями электрического поля и

эквипотенциальными линиями. Площадь элементарного четырехугольника ds=da·db, поэтому поток плотности вектора Пойнтинга через него

20