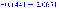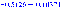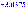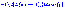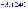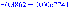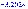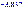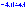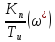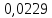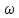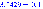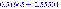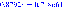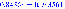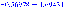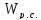zadacha
.docxФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО
ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МЭИ»
в г. Смоленске.
Кафедра промышленной теплоэнергетики
Задача
по курсу «Метрология, сертификация, технические измерения
и автоматизация тепловых процессов»
Преподаватель: Бобылев М.Г.
Студент: Хамдамов А.П.
Группа: ЭО-12
Вариант: 18
Смоленск 2015
Задание:
-
Рассчитать и построить графики
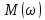 ,
,
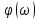 ,
,
 для
объекта с передаточной функцией
для
объекта с передаточной функцией
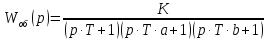
-
Определить критические значения частот
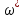 для П-регулятора и И-регулятора из
условия, что
для П-регулятора и И-регулятора из
условия, что
 .
.
Выполнить
аналитическим способом с применением
интерполяции и по графику
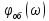 .
.
-
Определить критические значения параметров
 и
и
 для системы с П-регулятором и системы
с И-регулятором, при которых сиcтема
выходит на границу устойчивости при
условии
для системы с П-регулятором и системы
с И-регулятором, при которых сиcтема
выходит на границу устойчивости при
условии

-
Вычислить оптимальные (рабочие) параметры для П-регулятора и И-регулятора
 и
и
 из
условия
из
условия

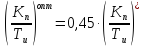
-
Рассчитать и построить
 для разомкнутой и замкнутой системы
по каналу управления
для разомкнутой и замкнутой системы
по каналу управления
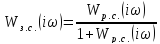
На
графиках отметить все частоты и выделить
резонансную частоту
 .
.
Исходные данные (табл.1).
Таблица 1
|
№ в журнале, Т, с |
К |
a |
b |
|
18 |
3,5 |
0,4 |
0,7 |
Решение
-
Рассчитать и построить графики
 ,
,
 ,
,
 для
объекта с передаточной функцией.
для
объекта с передаточной функцией.

Данную передаточную функцию можно рассмотреть как последовательное соединение трех инерционных звеньев с передаточными функциями:
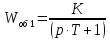

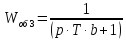
-
Рассмотрим первое инерционное звено:
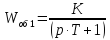 .
.
Для
определения фазы и амплитуды произведем
замену
 ,
получим:
,
получим:


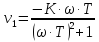
Амплитуда:


Частота:

-
Рассмотрим второе инерционное звено:
 .
.
Для
определения фазы и амплитуды произведем
замену
 ,
получим:
,
получим:

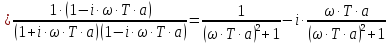


Амплитуда:
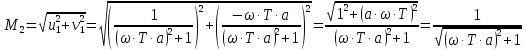
Частота:

-
Рассмотрим третье инерционное звено:
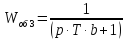 .
.
Для
определения фазы и амплитуды произведем
замену
 ,
получим:
,
получим:

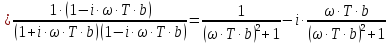


Амплитуда:
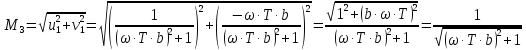
Частота:

При последовательном соединении:


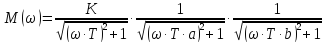
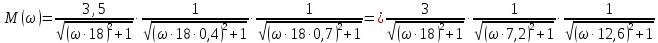
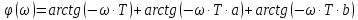


Общая передаточная функция для построения комплексной характеристики:


Строим
три полученные функции в программе
Maple.
Сведем значения
 ,
,
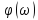 ,
,
 (табл.2).
(табл.2).
Таблица 2
|
|
|
|
|
|
0,0 |
|
|
|
|
0,01 |
|
|
|
|
0,02 |
|
|
|
|
0,03 |
|
|
|
|
0,04 |
|
|
|
|
0,05 |
|
|
|
|
0,06 |
|
|
|
|
0,07 |
|
|
|
|
0,08 |
|
|
|
|
0,09 |
|
|
|
|
0,1 |
|
|
|
|
0,11 |
|
|
|
|
0,12 |
|
|
|
|
0,13 |
|
|
|
|
0,14 |
|
|
|
|
0,15 |
|
|
|
|
0,16 |
|
|
|
|
0,17 |
|
|
|
|
0,18 |
|
|
|
|
0,19 |
|
|
|
|
0,2 |
|
|
|
|
0,21 |
|
|
|
|
0,3 |
|
|
|
|
0,4 |
|
|
|
|
0,5 |
|
|
|
|
0,6 |
|
|
|
|
0,7 |
|
|
|
|
0,8 |
|
|
|
|
0,9 |
|
|
|
|
1,0 |
|
|
|
|
2,0 |
|
|
|
Амплитудно-частотная
характеристика
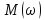 (рис.1)
(рис.1)

Рис. 1
Фазо-частотная
характеристика
 (рис.2)
(рис.2)

Рис. 2
Комплексно-частотная
характеристика (амплитудно-фазовая
характеристика)
 (Рис.3)
(Рис.3)

Рис. 3
-
Определить критические значения частот
 для П-регулятора и И-регулятора из
условия, что
для П-регулятора и И-регулятора из
условия, что
 .
.
Выполнить
аналитическим способом с применением
интерполяции и по графику
 .
.
Критическая
частота – частота, при которой система
превращается в генератор, когда сдвиг
фаз составляет
 .
.
Т.к.
П - регулятор дает сдвиг фаз в
 ,
,
 сдвиг в
сдвиг в
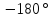 ,
следовательно
,
следовательно
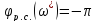 .
(чтобы в сумме было
.
(чтобы в сумме было
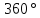 ).
).
Из таблицы значений:
|
ω |
φ |
|
0,15 |
|
|
0,16 |
|

Тогда
 при частоте
при частоте
 .
.
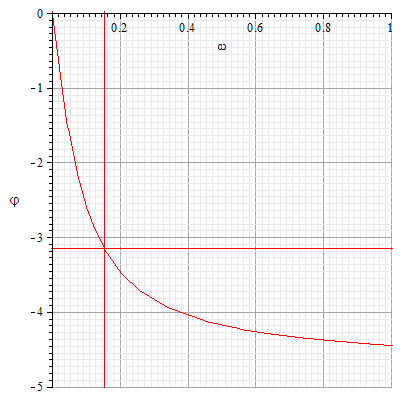
Рис.4. Критическая частота для П-регулятора.
Т.к.
И - регулятор дает сдвиг фаз в
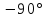 ,
,
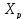 сдвиг в
сдвиг в
 ,
следовательно
,
следовательно
 .
(чтобы в сумме было
.
(чтобы в сумме было
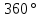 ).
).
Из таблицы значений:
|
ω |
φ |
|
0,04 |
|
|
0,05 |
|

Тогда
 при частоте
при частоте
 .
.

Рис.5. Критическая частота для И-регулятора.
Сравнивая
два метода нахождения критической
частоты
 для П- и И-регуляторов, а именно метод
интерполяции и графический метод, видим,
что полученные результаты практически
совпадают, т. е. методы имеют почти
одинаковую точность.
для П- и И-регуляторов, а именно метод
интерполяции и графический метод, видим,
что полученные результаты практически
совпадают, т. е. методы имеют почти
одинаковую точность.
-
Определить критические значения параметров
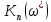 и
и
 для системы с П-регулятором и системы
с И-регулятором, при которых сиситема
выходит на границу устойчивости при
условии
для системы с П-регулятором и системы
с И-регулятором, при которых сиситема
выходит на границу устойчивости при
условии

-
П – регулятор


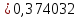
Тогда

Для
П-регулятора

-
И-регулятор

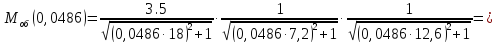
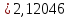
Тогда

Для И-регулятора:


|
П – регулятор |
|
|
|
И–регулятор |
|
|
-
Вычислить оптимальные (рабочие) параметры для П-регулятора и И-регулятора
 и
и
 из
условия
из
условия


-
П – регулятор
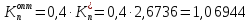
-
И–регулятор

-
Рассчитать и построить
 для разомкнутой и замкнутой системы
по каналу управления
для разомкнутой и замкнутой системы
по каналу управления
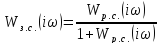 .
На графиках отметить все частоты и
выделить резонансную частоту
.
На графиках отметить все частоты и
выделить резонансную частоту
 .
.

-
П-регулятор
Т.к.
 ,
то
,
то

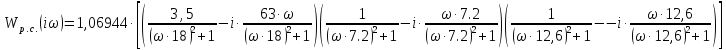

Составим
таблицы для
 и
и
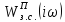 (табл.2)
(табл.2)
Таблица 2
|
|
|
|
|
0,0 |
|
|
|
0,01 |
|
|
|
0,02 |
|
|
|
0,03 |
|
|
|
0,04 |
|
|
|
0,05 |
|
|
|
0,06 |
|
|
|
0,07 |
|
|
|
0,08 |
|
|
|
0,09 |
|
|
|
0,1 |
|
|
|
0,11 |
|
|
|
0,12 |
|
|
|
0,13 |
|
|
|
0,14 |
|
|
|
0,15 |
|
|
|
0,16 |
|
|
|
0,17 |
|
|
|
0,18 |
|
|
|
0,19 |
|
|
|
0,2 |
|
|
|
0,4 |
|
|
|
0,6 |
|
|
|
0,8 |
|
|
|
1,0 |
|
|
Комплексная
характеристика
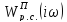 разомкнутой системы с П-регулятором
представлена на рисунке 6.
разомкнутой системы с П-регулятором
представлена на рисунке 6.
Определим резонансную частоту из графика:
 при
при


Рис.
6.
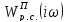
Комплексная
характеристика
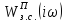 замкнутой системы с
П-регулятором представлена на рисунке
7.
замкнутой системы с
П-регулятором представлена на рисунке
7.
Определим резонансную частоту из графика:
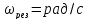 при
при


Рис.
7.

-
И-регулятор
Т.к.
 , то получаем
, то получаем




Составим
таблицы для
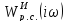 и
и
 (табл.3)
(табл.3)
Таблица 3
|
|
|
|
|
0,01 |
|
|
|
0,02 |
|
|
|
0,03 |
|
|
|
0,04 |
|
|
|
0,05 |
|
|
|
0,06 |
|
|
|
0,07 |
|
|
|
0,08 |
|
|
|
0,09 |
|
|
|
0,1 |
|
|
|
0,11 |
|
|
|
0,12 |
|
|
|
0,13 |
|
|
|
0,14 |
|
|
|
0,15 |
|
|
|
0,16 |
|
|
|
0,17 |
|
|
|
0,18 |
|
|
|
0,19 |
|
|
|
0,2 |
|
|
|
0,4 |
|
|
|
0,6 |
|
|
|
0,8 |
|
|
|
1,0 |
|
|