
II. Принцип Неопределенности Хайзенберга.
Вернер Хайзенберг, немецкий ученый, физик –теоретик, родился 5 декабря 1901 года в баварском городке Вюрцбург, Германская империя.
Вернер Хайзенберг провел множество исследований и изысканий , одним из результатов которых является открытое им и сформулированное правило. Его суть заключена в том , что невозможно одномоментно определить значения двух некоммутирующих характеристик механического движения частицы – скорости и координаты. Это означает, что с падением точности измерения одного параметра возрастает точность определения другого, причем эти изменения одинаковы по скорости.
Для наглядности можно проиллюстрировать явление графически:
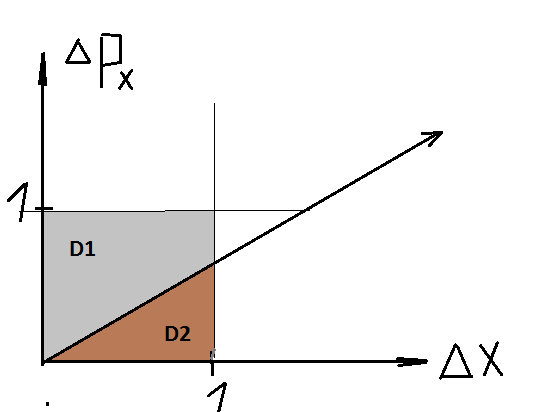 (I)
(I)
График (I) показывает ,что при абсолютно точном определении координаты страдает точность получения значения импульса. Это можно попытаться описать грубым соотношением частного площадей D1 и D2 и ΔX с ΔРх:
D1/D2 ~ ΔPx/ΔX; (4)
Другой способ иллюстрации предполагает введение единичной окружности и вектор- функции:
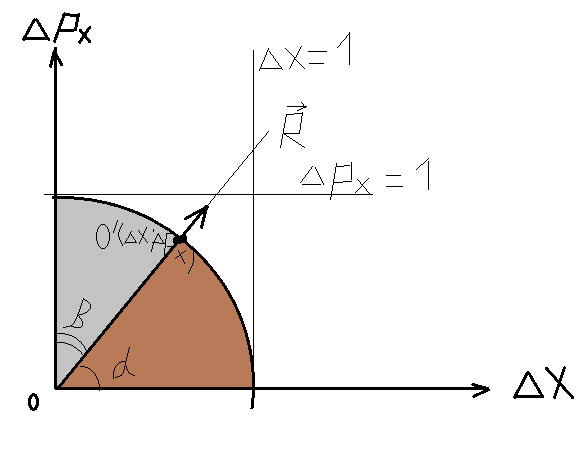 (II)
(II)
На
графике (II)
по оси абсцисс отложены значения ΔX
,по оси ординат – ΔРх. В точке О’ радиус-
вектор
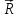 пересекает единичную окружность,
определенную в первой четверти
координатной плоскости. В зависимости
от соотношения неопределенностей
импульса и координаты точка О’ ”гуляет”
по дуге единичной окружности в пределах
[0;
пересекает единичную окружность,
определенную в первой четверти
координатной плоскости. В зависимости
от соотношения неопределенностей
импульса и координаты точка О’ ”гуляет”
по дуге единичной окружности в пределах
[0;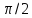 ]:
]:
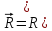 ∆X,
∆Px),
∆X,
∆Px),
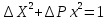 ,
,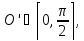
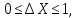 (5)
(6)
(5)
(6)
0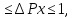
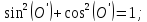 O’
O’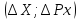 ;
;
Ее координаты представляют из себя пару значений погрешности измеряемых параметров. В силу природы явления неопределенностей даже при наличии абсолютно точного измерительного прибора и исследовательского метода их невозможно одновременно получить. Данные факты вполне согласуются с аппаратом специальной теории относительности Эйнштейна и преобразованиями Лоренса (где на скоростях ,близких к скорости света, изменяется конфигурация твердого тела- при известной скорости его длина получается с погрешностью).
При движении со скоростью света частица обладает волновыми свойствами. Де Бройль описал их через соотношения:
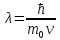 ,
,
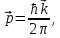 (7)
(7)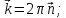
Где λ-
длина волны де Бройля,
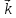 -
волновой вектор ,
-
волновой вектор ,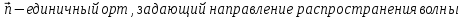 .
.
На рисунке проиллюстрировано колебательное движение частицы в пространстве ОХУ:
 (III)
(III)
С ростом ее скорости меняются ее колебательные характеристики- изменяется значение амплитуды колебаний и частоты:
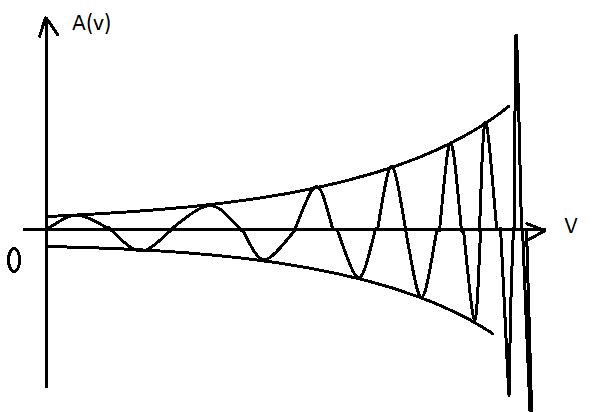 (IV)
(IV)

Исходя из теории корпускулярно- волнового дуализма , можно сказать, что частица одновременно может быть как волной, так и корпускулой. Этим и объясняется возможность наблюдения интерференционной картины пучка электронов на щели монокристалла.
Экспериментальные результаты подтверждают справедливость неоклассических методов теоретической физики начала двадцатого века.
III. Эффект Комптона.
10 сентября 1892 года в городе Вустер , штат Огайо, США, родился Комптон – физик- теоретик, нобелевский лауреат 1927 года.
С 1918 года ученый проводит исследования рентгеновского излучения . Результатом этих работ в последствии стал важный вывод: частицы имеют спин ,собственный момент импульса. Другими словами , частица имеет ось вращения . Учитывая квантовые эффекты ,описанные в этом реферате , частица колеблется вокруг своей оси, не имея однозначной траектории .
Эффект Комптона описывается как механическое взаимодействие излучения и элементарной частицы(γ-лучей и электронов). При анализе полагается, что электрон свободен и не обладает энергией связи, поэтому может получить порцию движения в виде импульса. При воздействии γ-луча на частицу его частота изменяется(падает),направление распространения волны меняется и луч отражается от первоначального направления под углом β, электрон получает импульс под углом α к линии первоначального направления волны, что видно из рисунка:
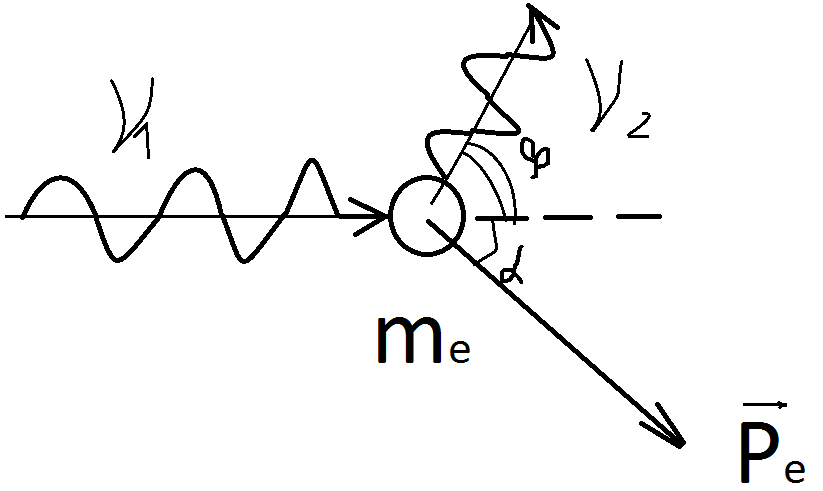 (I)
(I)
В данном случае справедлив закон сохранения энергии.
Обращаясь к классической механике, проведем аналогию: частица с массой m1 движется со скоростью V1 и сталкивается с покоящейся частицей массой m2. Из закона сохранения импульса следует:
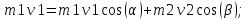 (8)
(8)
На основе этого можно предположить, что существует такая частица, которая ведет себя как волна и при этом сообщается с материальным объектом посредством импульса.
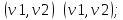
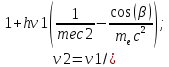 (9)
(9)
β- угол рассеяния;
Комптон первым доказал существование фотона, подтвердив теорию двойственности природы излучения. Он предположил, что рентгеновский луч обладает волновой и кинетической энергией :
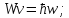
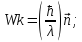 (10)
(10)
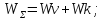
В
комптоновской теории не описывается
зависимость интенсивности рассеяния
от длины волны . В курсе квантовой
электродинамики такие случаи иллюстрируют
диаграммы Фейнмана. Можно описать
электрон в промежуточном состоянии-
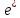 :
:
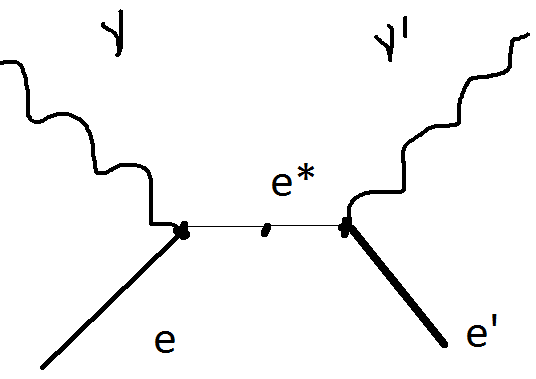 (II)
(II)
Здесь e и e’ – начальное и конечное состояния соответственно.
