romanovskiy_romanovskaya_elementy_teorii_veroyatnostey

время недостаточно ясны были области приложения теории вероятностей в естественных науках, то становится понятным, почему интерес к ней на Западе резко упал.

Третий период в развитии теории вероятностей тесно связан с работами Петербургской математической школы. Следует отдать должное выдающемуся математику В.Я.Буняковскому (1804–1889), роль которого в распространении вероятностных идей в России переоценить нельзя. Он является автором первого курса теории

праву можно назвать руководителем дореволюционной математической школы в России. Работы Чебышева в области теории вероятностей явились крупнейшим событием в математике. Они положили начало целому циклу глубоких исследований в области закона больших чисел. Его идеи оставили яркий след в развитии математики и предопределили надолго наперед направление и методы исследований массовых случайных явлений. "Вывел русскую теорию вероятностей на первое место в мире Пафнутий Львович Чебышев", – так оценил роль этого замечательного ученого академик А.Н. Колмогоров13.

Наиболее выдающимися учениками Чебышева, оставившими неизгладимый след в развитии теории вероятностей, являются А.А. Марков14 и А.М. Ляпунов15. Маркову

12П. Л. Чебышев (1821–1894) – создатель целой математической школы в России. Он сыграл большую и в ряде случаев решающую роль в развитии многих областей математики. Работы Чебышева в области теории приближения функций многочленами, теории чисел, теории интегрирования и теории вероятностей позволяют поставить его имя в ряд с именами величайших математиков всех времен.

13А.Н. Колмогоров (1903–1987) – один из самых замечательных ученых ХХ века, внесший огромный вклад в развитие математики и ее приложения.

14А.А. Марков (1856 –1922) – один из выдающихся представителей математической школы, созданной Чебышевым. Имеет работы в различных областях математики; основные его достижения в

11

принадлежит обобщение закона больших чисел на случай зависимых случайных величин. Его работы положили начало бурно развивающейся в настоящее время теории случайных функций. Ляпунову мы обязаны первым доказательством

центральной предельной теоремы при весьма общих условиях.

Современный, четвертый период характеризуется исключительным подъемом интереса к теории вероятностей в самых различных областях человеческой деятельности. Этот интерес стимулировал бурное развитие многих направлений теории вероятностей.

Российская школа теории вероятностей, которая в настоящее время по праву занимает в мировой науке ведущее место, решила ряд принципиальных вопросов. В частности, академикам С. Н. Бернштейну и А. Н. Колмогорову принадлежат основополагающие работы в аксиоматическом построении теории вероятностей.

Большой вклад в развитие теории вероятностей внесли российские ученые А.Я. Хинчин, Б.В. Гнеденко, Е. Б. Дынкин, В.С. Пугачев, А.Н. Ширяев, А.А. Боровков, Ю.А. Розанов, Ю.В. Прохоров, И.И.Гихман, А.В. Скороход и другие. Теория вероятностей продолжает интенсивно развиваться в настоящее время.

области теории вероятностей, которой он посвятил более 25 работ. его деятельность привела к полному решению основных вопросов теории вероятностей: предельных теорем, закона больших чисел и способа наименьших квадратов. Как отметил академик В.А. Стеклов, трудность этих вопросов не могла быть преодолена в науке до Маркова в течение многих десятилетий.

15 А. М. Ляпунов (1857–1918) – один из наиболее выдающихся русских математиков и механиков, ближайший ученик Чебышева. Он создатель теории устойчивости движения, методов качественной теории дифференциальных уравнений, метода характеристических функций в теории вероятностей.

12

Глава 1. Основные понятия и правила теории вероятностей

§ 1. Классическое определение вероятности

Пусть с испытанием связано интересующее нас событие А. Событие А называется случайным, если оно может произойти или не произойти при данном испытании в зависимости от случая; достоверным, если оно при данном испытании заведомо произойдет; невозможным, если оно заведомо не произойдет.

Далее будем использовать стандартные обозначения: Ω – достоверное событие;– невозможное событие.

Общее определение вероятности случайного события дано в опубликованной в 1933 г. фундаментальной работе академика А.Н. Колмогорова "Основания теории вероятностей". Это определение сложно для понимания. Мы ограничимся так называемым классическим определением вероятности, данным еще в XVIII в. Ферма и Паскалем, и относящимся к частной ситуации. Правила теории вероятности, основанные на этом определении, остаются верными и в общем случае.

Пусть испытание имеет n равновозможных исходов (в

зависимости от случая), из которых интересующему нас событию А благоприятствуют т исходов.

Определение. Вероятностью события А при данном испытании называется отношение числа благоприятных исходов к числу всех равновозможных исходов:

Данное определение носит название классического определения вероятности.

13

Пример 1. Испытание: бросают монету один раз. Событие А: выпадение герба.

Р (А) - ?

P( A) = m = 1 = 50% . n 2

Пример 2. Испытание: бросают монету два раза. Событие А: одинаковый результат.

Р (А) - ?

P( A) = m = 2 = 1 = 50% . n 4 2

Очевидно, данное испытание имеет четыре равновозможных исхода: ГГ, ЦЦ, ГЦ, ЦГ (Г – герб, Ц – цифра).

Пример 3. В урне имеется 10 белых и 5 черных шаров. Испытание: берут наугад один шар равновозможным

образом.

Событие А: шар белый

Р (А) - ?

P( A) = 10 = 2 . 15 3

Замечание 1. Р ( ) = 0 = 0 ; n

Р (Ω) = n = 1 = 100% ; n

0 ≤ Р (А) ≤ 1.

Замечание 2. Укажем реальный смысл понятия "вероятность". Предположим, что вероятность связанного с некоторым испытанием случайного события А равна 30%. Это позволяет сделать следующий прогноз: если испытание повторять достаточно много раз, то с практической достоверностью событие А произойдет примерно в 30% случаях, причем этот прогноз тем точнее, чем больше число испытаний. Помнить: вероятность случайного события – это процент наступления события в длинной серии одинаковых независимых испытаний. Точная формулировка и

14

доказательство этого утверждения приводятся далее в §2 главы 5; см. также §1 введения.

Геометрическое определение вероятности

P( A) = m = ∞ не имеет смысла. n ∞

По определению примем:

§ 2.Элементы комбинаторики

Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего, в частности, вопрос о количестве комбинаций из n элементов по т, которые можно составлять тем или иным способом. Мы рассмотрим три таких способа.

1. Сочетания

Комбинации из n элементов по т, отличающиеся только составом, называются сочетаниями. Число сочетаний из n элементов по т равно

где n! = 1× 2 ×K× n .

15

Пример 1. В группе 30 человек. Необходимо выбрать трех делегатов на конференцию. Сколько существует

способов это сделать?

Решение. Каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки отличаются только по составу, то есть являются сочетаниями из 30 элементов по 3.Их количество находим по формуле (2):

Пример 2. В шахматном турнире участвует 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна

одна партия?

Решение. Каждая партия играется двумя участниками из 16. Пары игроков отличаются от других пар только составом, то есть представляют собой сочетания из 16 элементов по 2. По формуле (2) найдем:

2. Размещения

Комбинации из n элементов по т, отличающиеся составом или порядком элементов, называются размещениями. Число размещений из n элементов по т равно

Пример 1. В группе 30 человек необходимо выбрать старосту, его заместителя и профорга. Сколько существует

способов это сделать?

Решение. Каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки

16

отличаются как по составу, так и по порядку, то есть являются размещениями из 30 элементов по 3. Их количество находим по формуле (3):

A303 = 30! = 28 × 29 ×30 = 24360 способов. 27!

Пример 2. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе 11 дисциплин.

Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания, то есть число размещений из 11 по 5 находим по формуле (3):

A115 = 11! = 7 ×8 ×9 ×10 ×11 = 55440 вариантов. 6!

3. Перестановки

Комбинации из n элементов по n, отличающиеся порядком, называются перестановками. Число перестановок из n элементов равно

Пример 3. Порядок выступления семи участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, то есть является перестановкой из 7 элементов. Их число находим по формуле (4):

P7 = 7!= 1× 2 ×3 × 4 ×5 ×6 ×7 = 5040 вариантов.

Приведем пример на вычисление вероятности случайного события с использованием формул комбинаторики.

17

Пример 4. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3

студента – разрядники?

Решение. Пусть событие А состоит в том, что все 3 выбранных наудачу студента – разрядники. Общее число

вариантов выбора трех студентов из 30 равно n = C303 , так

как комбинации из 30 студентов по 3 отличаются только составом студентов. Точно так же число случаев,

§ 3. Действия над событиями

Пусть с испытанием связаны события А, В. Определение 1. Суммой событий А, В называется

третье событие С, состоящее в наступлении хотя бы одного из событий А, В:

С = А + В.

Пример 1. Испытание: берут наугад точку в области D

Рис. 2 область.

Тогда С = А + В.

Определение 2. Произведением двух событий А, В называется третье событие С, состоящее в одновременном наступлении этих событий: С = А · В.

18

Пример 2. Испытание: берут наугад точку в области D (рис 2). Рассмотрим события:

А – попадание в область d1;

В – попадание в область d2;

С– попадание в общую часть областей d1 и d2. Тогда С = А · В.

Определение 3. Событие В называется противоположным событию А, если оно состоит не в наступлении события А:

В = A .

Пример 3. Испытание: берут наугад точку в области D

Замечание. Укажем другие обозначения для введенных операций:

А+ В Û А или В;

А· В Û А и В;

A Û не А.

Сумма событий – операция "или"; произведение событий – операция "и";

переход к противоположному событию – операция "не".

Из определения суммы и произведения событий вытекают следующие свойства введенных трех операций.

Докажем свойства 12 и 13, остальные 1–11 очевидны. Событие А + В состоит в наступлении хотя бы одного

19

ненаступлении хотя бы одного из событий А или В. Тот же

свойствам, называется алгеброй Буля. Алгебра Буля играет важную роль в математической логике, являющейся одной из теоретических основ ЭВМ.

В математической логике применяются следующие названия указанных операций: "или" – дизъюнкция; "и" – конъюнкция; "не" – отрицание.

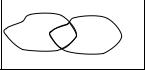
§ 4. Теоремы сложения и умножения вероятностей

Теорема 1. Пусть с испытанием связаны события А, В. Справедлива формула:

Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.

Доказательство. Проведем доказательство в рамках

20