
предел функции тд
.pdf
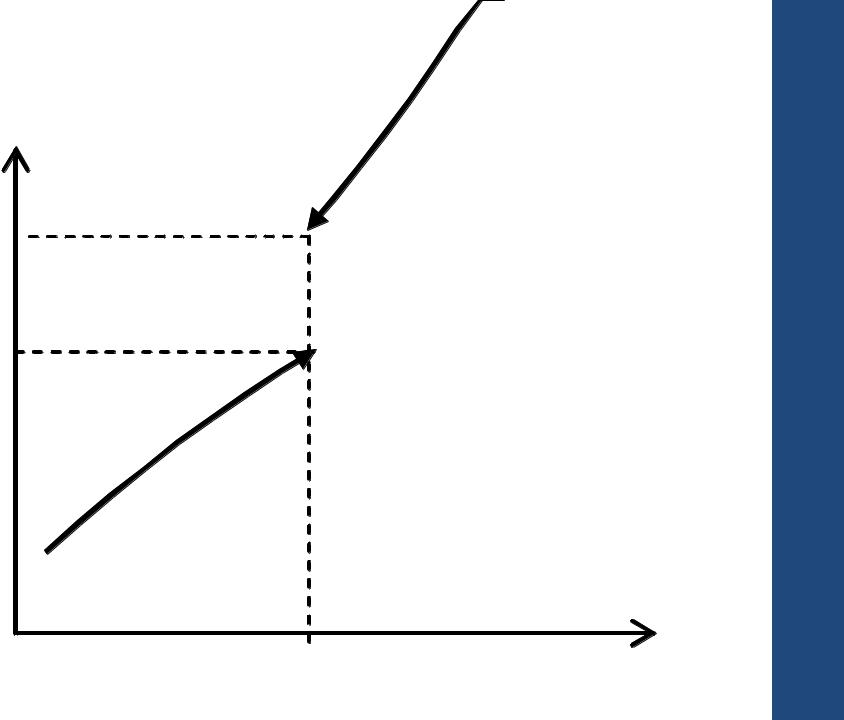
Число С называется пределом слева
функции f(x) в точке b (это записывается в |
|
виде формулы |
C lim f x |
|
|
|
x b0 |
если для любого положительного числа |
|
найдется положительное число такое, что из условия
0 < b – x < будет следовать C – f(x) < .
21
У
x)
В
С
О |
а |
Х |
|
|
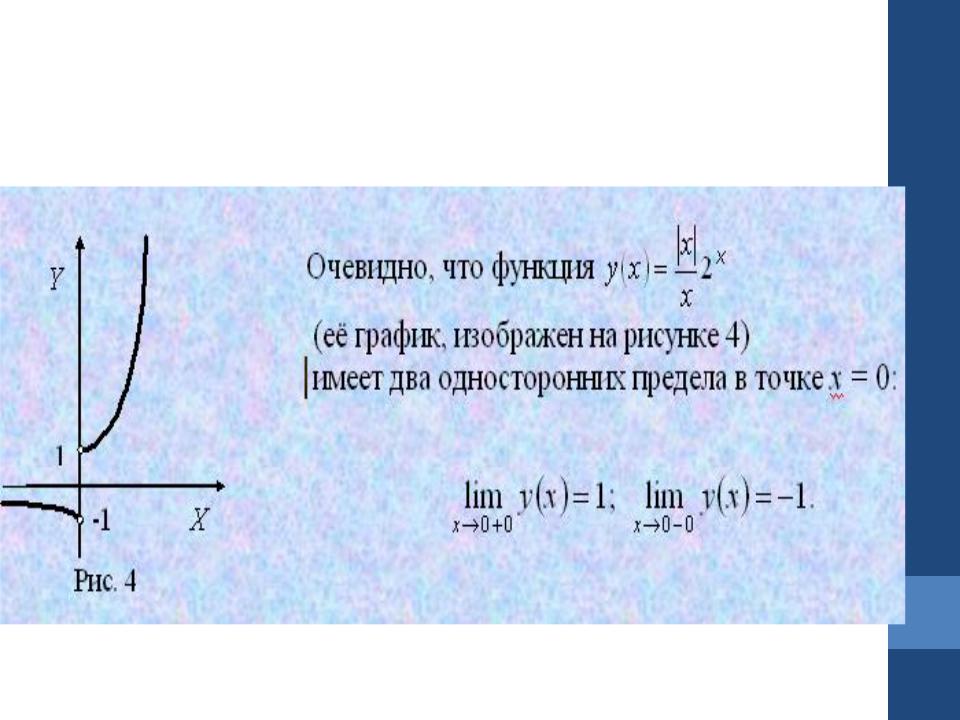

Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если
|
lim |
f x f a |
|
x a 0 |
|
( |
lim |
f x f b ) |
x b 0 |
||
24

Правила предельного перехода

1. Предел суммы (разности) двух функций, имеющих предел, равен сумме (разности) пределов этих функций:
|
|
|
lim ( f (x) (x)) lim |
f (x) lim (x) A B |
|
x a |
x a |
x a |
•2. Предел произведения двух функций, имеющих предел, равен произведению пределов этих функций:
|
|
|
|
|
lim ( f (x) (x)) lim |
f (x) lim (x) A B |
|
• |
x a |
x a |
x a |
3. Постоянный множитель можно вынести до знака |
|||
предела: |
|
|
|
|
|
|
||
lim (cf (x)) c lim |
f (x) cA |
|
|
|
x a |
x a |
|
|
|
|
|
|
||
|
|
|
|
|

4. Предел константы равен константе:
|
|
lim c c, где |
c const |
x a |
|
•5. Предел отношения двух функций, имеющих предел, равен отношению пределов этих функций:
|
f (x) |
|
lim f (x) |
|
A |
|
|
|
lim |
|
x a |
|
, |
lim (x) 0 |
|||
|
lim (x) |
|
|
|||||
x a (x) |
|
|
B |
|
x a |
|||
|
|
|
x a |
|
|
|
|
|
• 6. Для всех основных элементарных функций в любой точке их области определения имеет место
|
|
|
|
lim |
f (x) f (lim x) f (a) |
|
|
|
|||
x a |
x a |
|
|
|
|
|
|

Бесконечно малые и бесконечно большие функции

О п р е д е л е н и е 1.
•Функция у = f (x) называется
бесконечно малой (Б.М.Ф.)
•при х а,
•если ее предел равен нулю
|
|
|
|
lim |
f ( x) 0 f ( x) Б.М.Ф. |
|
|
x a |
при x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
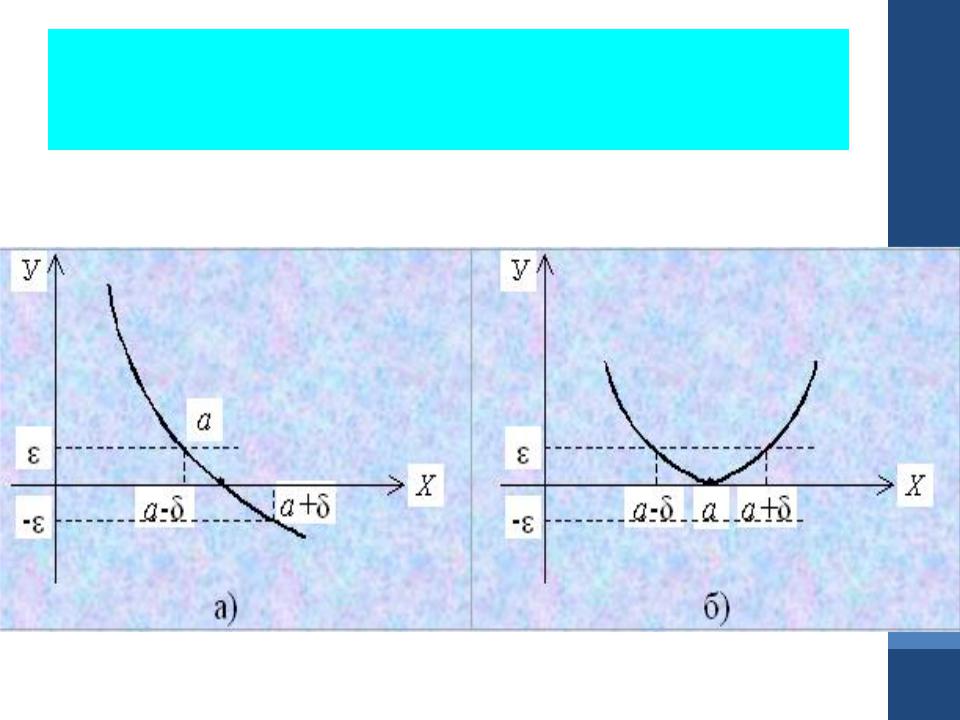
Геометрически это означает, что функция либо пересекаетось ОХ, либо касается ее в точке х=а.
