1. Классификация режимов

Режимом электрической системы называется ее состояние в какой-либо момент времени или на каком-либо интервале времени.

Переменные, характеризующие состояние системы, называются параметрами режима (см. п. 1.2). В зависимости от изменения параметров режима во времени различают установившиеся и переходные режимы.

Установившимся называется режим, параметры которого неизменны во времени или меняются по периодическому закону. Так, в электрических сетях переменного тока в установившемся режиме мгновенные значения токов и напряжений изменяются во времени по синусоидальному закону. При этом действующие значения остаются постоянными.

Переходные режимы (процессы) возникают при любых изменениях в системе и характеризуются непериодическим изменением параметров режима во времени. Наличие этих процессов обусловлено инерционностью системы. Они протекают при переходе от одного установившегося режима к другому. В некоторых случаях изменения приводят к тому, что нового установившегося режима не существует. Тогда переходный процесс приводит к «развалу» системы.

По условиям возникновения режимы электрических систем подразделяются на нормальные, аварийные, послеаварийные и ремонтные.

Нормальным называется установившийся режим, возникающий при нормальной схеме коммутаций в системе, причем параметры режима находятся в технически допустимых пределах.

Аварийным называется режим, возникающий в момент возникновения аварии и продолжающийся до ее устранения. Эти режимы в начальный момент времени всегда являются переходными; затем, при достаточной продолжительности аварии, они могут переходить в установившиеся.

Послеаварийным называется режим, который возникает после устранения аварии. Обычно при этом имеется в виду установившийся режим. Параметры послеаварийных режимов могут как находиться в технически допустимых пределах, так и выходить за эти пределы. В отдельных случаях послеаварийные режимы являются автоколебательными (действующие значения токов и напряжений меняются во времени по периодическому закону).

Ремонтным называется установившийся режим, возникающий после планового вывода в ремонт какого-либо элемента системы. В целом эти режимы сходны с послеаварийными, однако параметры ремонтных режимов должны находиться в технически допустимых пределах.

Кроме того, отдельно выделяются особые режимы электроэнергетических систем. К ним относятся:

1) режимы, параметры которых выходят за технически допустимые пределы, в частности несимметричные и несинусоидальные режимы;

2) режимы холостого хода линий электропередачи;

3) режимы, близкие к пределу по статической устойчивости;

4) различные неустойчивые режимы, в том числе автоколебательные.

2. Параметры установившихся режимов

Состояние электрической системы в установившихся режимах характеризуются следующими параметрами:

1. Напряжения в узлах сети. В сетях переменного тока в качестве напряжений рассматриваются комплексы их действующих значений. При допущении, что режим трехфазной сети является симметричным и синусоидальным, используются напряжения , равные по модулю линейным напряжениям, а по фазе – фазным напряжениям. В несимметричных режимах используются либо симметричные составляющие напряжений,,, либо фазные напряжения,,. В несинусоидальных режимах используются гармонические составляющие напряжений, гдеν – номер гармоники.

2. Токи в ветвях схемы замещения электрической сети: в сетях переменного тока – комплексы действующих значений ; в несимметричных режимах – симметричные составляющие токов,,или фазные токи,,; в несинусоидальных режимах – гармонические составляющие токов.

3. Мощности, передаваемые по элементам сети. В сетях постоянного тока существует только активная мощность P, а в сетях переменного тока – активная, реактивная и полная мощности P, Q и . В трехфазных сетях при расчетах обычно используются суммарные мощности, передаваемые по всем трем фазам. В симметричных режимах

, (1.1)

где индекс «*» обозначает сопряженный комплекс.

В несимметричных режимах

. (1.2)

Выразим мощность в симметричном режиме через напряжения и параметры сети. Пусть ветвь схемы замещения соединяет узлы с номерами i, j, напряжения в которых равны ,(рис. 1.1). Ток в ветви, направленный от узлаi к узлу j,

, (1.3)

где Y_ij – комплексная проводимость ветви.

Тогда мощность в начале ветви (со стороны узла j), передаваемая в направлении от узла i к узлу j,

. (1.4)

Аналогично выразится мощность в конце ветви (со стороны узла j), передаваемая в том же направлении:

. (1.5)

4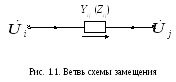. Мощности, генерируемые ис-точниками питания, в общем случае определяются по формуле (1.1). Для некоторых источников мощности заданы заранее и, таким образом, являются исходными данными для расчетов.

5. Мощности потребителей (нагрузки). В общем случае эти мощности зависят от уровня напряжения у данного потребителя в соответствии со статическими характеристиками P = f(U), Q = g(U). Часто статические характеристики по напряжению аппроксимируются полиномами второй степени. Тогда

, (1.6)

, (1.7)

где ;U_ном – номинальное напряжение; Р_ном и Q_ном – мощности, потребляемые при номинальном напряжении; a₁, a₂, a₀, b₁, b₂, b₀ – коэффициенты аппроксимации, причем ,.

Часто нагрузки задаются в форме Р = const, Q = const. В этом случае их мощности являются исходными данными для расчета режимов.

6. Потери мощности в элементах сети. В трехфазной сети в симметричном и синусоидальном режиме для ветви с комплексным сопротивлением Z_ij (рис. 1.1) потери полной мощности, приходящиеся на все три фазы, могут быть определены следующими способами:

. (1.8)

7. Потери энергии. Они представляют собой интегральный параметр, определяющийся не одним режимом, а их совокупностью, реализованной за некоторый интервал времени T. Потери энергии ΔW связаны с потерями активной мощности ΔP соотношением

, (1.9)

где время t обычно выражается в часах.

На практике вместо формулы (1.9) для расчета потерь энергии обычно используются упрощенные подходы.

8. Частота тока f. Данный параметр определен при условии, что мгновенные значения токов и напряжений являются периодическими функциями времени, в частности, синусоидами. Строго говоря, это условие выполняется только в установившихся режимах. Однако при переходных режимах, имеющих электромеханическую природу, электромагнитными процессами часто можно пренебречь. Тогда напряжения и токи также рассматриваются как периодические функции.

В большинстве случаев при расчете режимов частота тока принимается постоянной. Исключением являются некоторые аварийные и особые режимы.