АГ Векторная алгебра 2015-16 / Практическое занятие 1+СР(действия над векторами)
.doc
Практическое занятие № 1
Действия над векторами
-
Найти на рисунке все тройки векторов, которые удовлетворяют равенству:
,
записать соответствующие равенства.
-
В параллелограмме ABCD точка K делит сторону AB в отношении 3:1, а точка L делит сторону CD в отношении 2:3. Выразить через векторы, лежащие на сторонах параллелограмма:
-
вектор
, -
вектор
, -
вектор
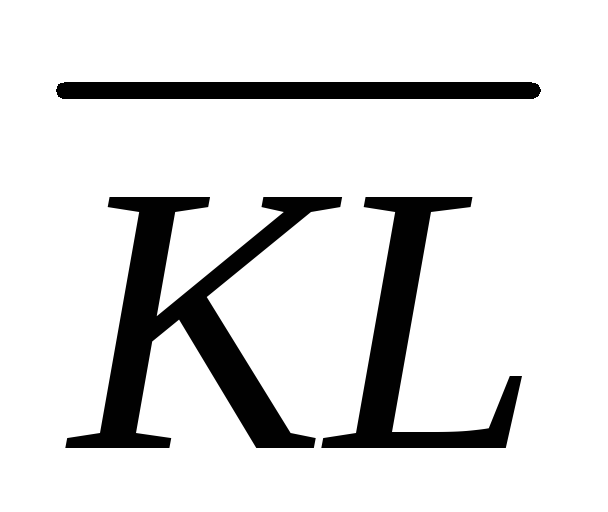двумя способами.
-
-
Доказать, что сумма всех векторов с общим началом в центре правильного многоугольника и концами в его вершинах равна нулю.
-
Векторы
и
совпадают с медианами треугольника
ABC.
Выразить векторы, совпадающие со
сторонами треугольника, через
и
.
-
В равнобедренной трапеции ABCD точка O – точка пересечение диагоналей, коэффициент подобия треугольников AOD и BOC равен k,
,
.
Найти разложение вектора
в линейную комбинацию векторов
,
. -
Из точки O выходят два вектора
Найти какой-нибудь вектор
идущий по биссектрисе угла AOB. -
В правильном восьмиугольнике ABCDEFGH
.
Выразить через
и
векторы, совпадающие с остальными
сторонами восьмиугольника.
Задание №1 по векторной алгебре для самостоятельной работы
-
На плоскости дан
.
Найдите точку O
этой плоскости такую, что
. -
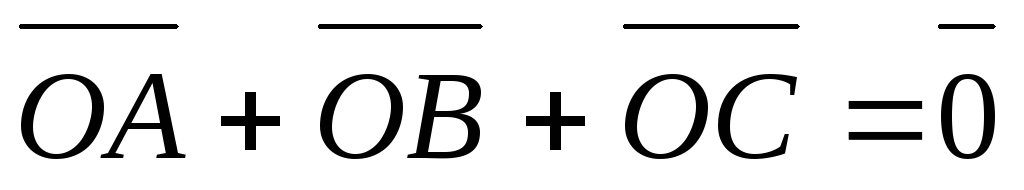На плоскости даны параллелограмм
и произвольная точка O.
Доказать, что
.
Доказать обратное утверждение: если
для некоторого плоского четырехугольника
ABCD
и точки O
имеет место соотношение
,
то ABCD
– параллелограмм. -
Доказать, что стороны АВ и DC четырехугольника ABCD параллельны тогда и только тогда, когда отрезок MN, соединяющий середины этих сторон проходит через точку O пересечения диагоналей.
-
В DABC точка M делит сторону AB в отношении 3:5, а точка K делит сторону BC отношении 3:1. Выразить вектор
через векторы
и
.
Ответ:
-
В треугольнике ABC точка M – точка пересечения медиан,
,
.
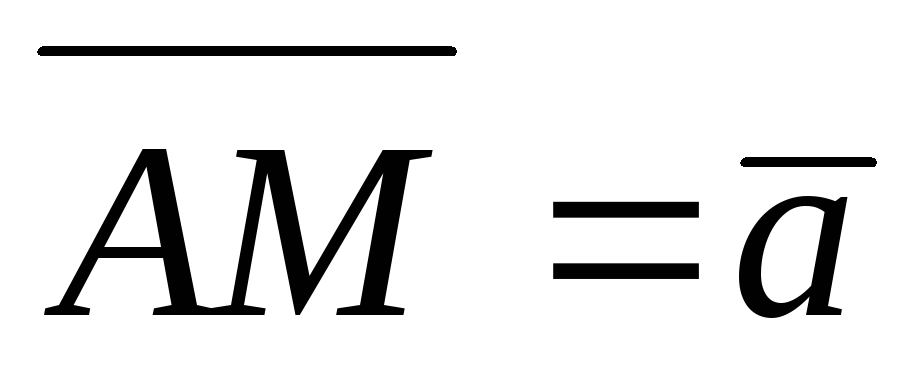Выразить через
и
векторы
и
.
Ответ:
-
Зная радиус-векторы трех последовательных вершин параллелограмма, найти:
-
радиус-вектор точки пересечения его диагоналей;
-
радиус-вектор четвертой вершины.