Упражнения

1. Используя циклы с предусловием, с постусловием, с параметром составить три варианта программы вычисления N!.

2. Составить программу, по которой будет вводиться последовательность целых чисел до тех пор, пока не встретится число 9999. Подсчитать количество введенных значений и их сумму.

3. Вычислить сумму квадратов всех целых чисел, попадающих в интервал (ln x, e^x), x > 1.

4. Вычислить количество точек с целочисленными координатами, попадающих в круг радиуса R (R > 0) с центром в начале координат.

5. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.

6. Дано целое n > 2. Напечатать все простые числа из диапазона [2, n].

7. Рекуррентная последовательность определена следующим образом:

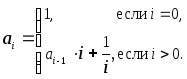
Для данного натурального n получить значение a_n.

8. Дана последовательность:

Вычислить произведение элементов с 1-го по 20-й.

9. Используя рекуррентный подход, вычислить сумму многочлена 10-й степени по формуле Горнера, где x –– данное вещественное число.

10x¹⁰ + 9x⁹ + 8x⁸ + ... + 2x² + x = (((((((((10x + 9)x + 8)x + ... + 2)x + 1)x.

10. Для данного вещественного x и натурального N вычислить цепную дробь: x / (1 + x / (2 + x / (3 + x / ( ... / (N + x))...).

5. Вычислить и вывести все члены числового ряда

превышающие значение 10^–5.

11. Функцию можно вычислить как предельное значение последовательности, определяемой рекуррентной формулой

Начальное значение y₀ задается произвольно (желательно ближе к). За приближенное с точностью значение корня берется первое y_k, для которого выполняется условие: |y_k – y_k-1| < . Составить программу.

72