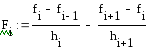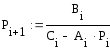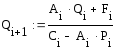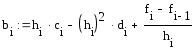Лабораторная работа №6

Используя записанную таблично функцию из предыдущей работы ( под буквой «а»), с помощью первой и второй интерполяционной формулы Ньютона найти приближенное значение функции при заданных значениях аргумента ().

	x1=	x2=
	0,14	0,53
	0,16	0,47
	0,4	0,04
	0,1	0,3
	1,15	1,65
	0,95	0,38
	0,5	-0,42
	63	98
	1,2	5,7
	3,55	4,55
	0,5	1,45
	0,026	0,046
	0,22	0,51
	1,1	-3,9
	10	77
	1,23	1,75
	1	5,2
	0,33	0,72
	0,77	1,37
	0	1,55
	0,4	-0,42
	0,9	0,7
	19,5	1,25
	2	0,16
	0,39	1,74
	0	7,5
	11	0
	1	10,5
	0,8	-1
	0,25	-0,55

Сплайн интерполяция

Сплайн функция  сплайн  кусочно-полиномиальная функция, проходящая через заданное множество узлов интерполяции и имеющая в данной области некоторое количество непрерывных производных.

В вычислительной практике распространено использование кубических сплайнов. Приближение функции с помощью кубического сплайнадолжно удовлетворять следующим условиям: 1)функция многочлен третьей степени; 2) функции ,,непрерывны на заданном отрезке; 3) , согласно условию интерполирования.

Для любого задается функцияв виде многочлена третьей степени:

,

где коэффициенты, подлежащие определению.

С учетом выше перечисленных условий, а так же двух дополнительных (для концов заданного отрезка) ,, коэффициенты записываются:

, ;

, , ;

,

, .

Здесь ,.

В образованной системе уравнений, коэффициенты можно определить из последней строки методом прогонки. Остальные коэффициенты выражаются через найденные. Рассмотрим метод прогонки для нахождения коэффициентов. Последнее уравнение системы это уравнение (при ) вида:

, ,

где ,,,.

Если привести это уравнение к виду:

, , то

, , .

В двух последних строках заключена суть метода прогонки: сначала находятся все коэффициенты (необходимо знать ), затем находятся значения (необходимо знать ). Так как , а , то . С другой стороны .

Ниже приведен пример вычисления коэффициентов полинома для функции заданной таблично. Этот же пример использован при рассмотрении полиномиальной интерполяции Лагранжа.

i	xi	fi	hi
0	0,05	0,05004
1	0,1	0,10034	0,05
2	0,17	0,17166	0,07
3	0,25	0,25534	0,08
4	0,3	0,30934	0,05
5	0,36	0,37640	0,06

Сначала вычисляются прогоночные коэффициенты.

i	Ai	Bi	Ci	Fi	Pi	Qi
0
1	0,01667	0,023333	-0,08	-0,01303	0	0
2	0,02333	0,026667	-0,1	-0,02718	-0,29167	0,162821
3	0,02667	0,016667	-0,08667	-0,03382	-0,28614	0,250848
4	0,01667	0,02	-0,07333	-0,0379	-0,21087	0,343238
5					-0,28646	0,460946

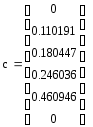
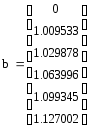
Затем вычисляются коэффициенты , и все остальные коэффициенты полинома.

i	ci		di	bi	ai
0	0				0,050042
1	0,1101911		0,734607	1,009533	0,100335
2	0,1804469		0,334552	1,029878	0,171657
3	0,2460363		0,273289	1,063996	0,255342
4	0,4609463		1,432734	1,099345	0,309336
5	0		-2,56081	1,127002	0,376403

Для того, чтобы вычислить функцию в точке, необходимо вычислить полином

в этой точке.

, что с точностью до трех знаков после запятой совпадает с раннее вычисленным значением по интерполяционной формуле Лагранжа.

Ниже этот же пример решен с помощью системы MathCAD.