3.3. Упражнения.
3.3.1. Доказать, что следующие множества образуют кольцо относительно указанных операций. Какие из них являются ассоциативными, коммутативными, кольцом с единицей. Какие из них образуют поле?
а) Множество целых чисел Z относительно сложения и умножения.
б) Множество Mn(R) квадратных матриц размерности n относительно сложения и умножения матриц.
в) Множество nZ={nk | kZ} чисел, кратных n, где n фиксированное натуральное число, n2, относительно сложения и умножения чисел.
г) Множество векторов трёхмерного физического пространства относительно сложения и векторного умножения.
д) Множество Zm классов вычетов по модулю целого числа m2 относительно операций сложения и умножения классов, определённых по правилам
.
е) Множество Qрациональных чисел,Rдействительных чисел, комплексныхCчисел.
3.3.2. Доказать, что элементы кольца и поля образуют абелеву группу относительно сложения. Эти группы называются аддитивной группой соответственно кольца и поля.
3.3.3. Доказать, что ненулевые элементы поля образуют абелеву группу относительно умножения. Эта группа называется мультипликативной группой поля. Мультипликативная группа поля F обозначается через F *.
3.3.4. Доказать, что в определении коммутативного кольца условие 5) лишнее.
3.3.5. Построить таблицы сложения и умножения для колец Z2, Z3, Z4, Z5, Z6, Z7, Z8. Какие из них являются полями, какие нет? Какие являются областями целостности? Найти также в каждом из них делители нуля и для всех элементов обратные и противоположные.
Решение. Построим таблицу сложения для Z4:
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например,
+
=
=
,
+
=
=
=
.
Так как
+
=
,
+
=
+
=
,
+
=
,
то
=
,
=
,
=
,
=
.
Построим таблицу умножения для Z4:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например,
=
=
,
=
=
.
Как
видим, элемент
не имеет обратного, так как ни одно
произведение вида
х
не равно
.
Значит, кольцоZ4
не является полем. Так как
=
=
,
то
=
и
=
.
Так
как
=
,
в то время как
,
то
является делителем нуля, то есть в кольцеZ4
имеются
делители нуля и данное кольцо не является
областью целостности.
Аналогично для Z5:
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так
как
+
=
+
=
+
=
+
=
+
=
,
то
=
,
=
,
=
,
=
,
=
.
Таблица умножения для Z5:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечаем,
что в каждой строке и каждом столбце
для ненулевых элементов имеется единичный
элемент
.
Это означает, что каждый ненулевой
элемент кольцаZ5
имеет обратный. Например,
=
,
то есть
=
и
=
.
Аналогично,
=
,
=
.
Следовательно,Z5
это поле.
Также замечаем, что в Z5 нет делителей нуля. Поэтому Z5 область целостности.
Ответ:
Z4
ни областью целостности, ни полем не
является. При этом 
=
,
=
,
=
,
=
,
=
и
=
.
Элемент
является делителем нуля.
Кольцо
Z5
является полем и областью целостности.
При этом 
=
,
=
,
=
,
=
,
=
,
=
,
=
,
=
,
=
.
3.3.6. Для АMn(R) найти левые и правые делители нуля:
а)
А=
(n=2);
б) А=
(n=2);
в) А=
(n=3);
г)
А=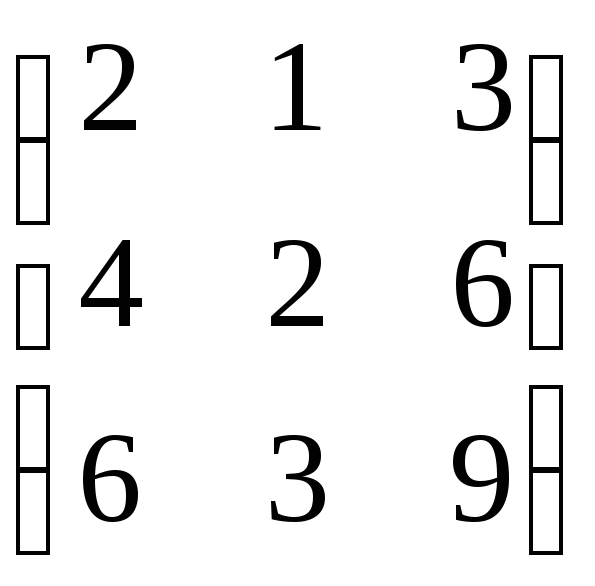
(n=3);
д) А=
(n=3).
Решение.
а) Пусть B=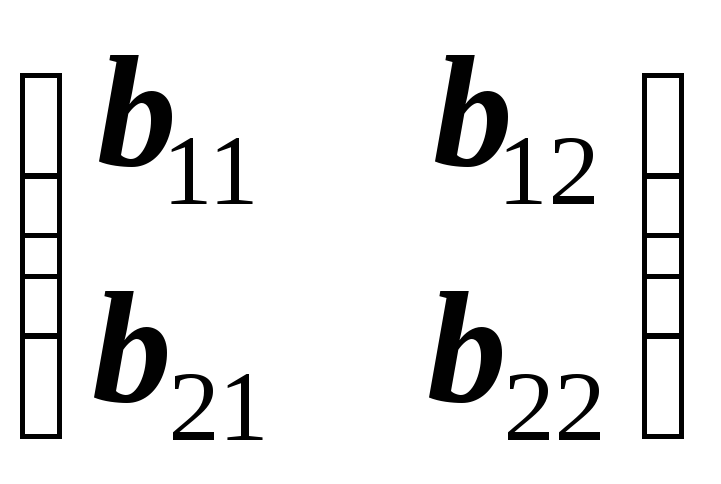
правый делитель нуля для А=
.
Это означает, чтоB≠O
и AB=O,
где O=
.
Имеем
AB=
=
.
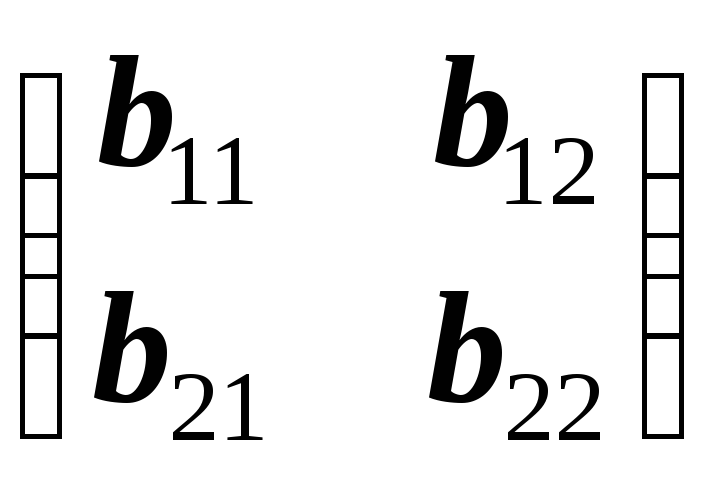Тогда
AB=O
равносильно
=
,
что в свою очередь равносильно системе
однородных уравнений
Третье и четвёртое уравнения получаются из первого и второго (соответственно) умножением на 3. Поэтому эта система равносильна системе
Взяв
в этой системе в качестве свободных
неизвестных b21=
и b22=,
получаем множество решений (;
;
;
),
где
и
одновременно не обращаются в 0, то есть
B=
,
где 2+2≠0,
являются правыми делителями нуля матрицы
А=
в кольцеM2(R).
Аналогично находим левые делители нуля:
BA=O
=
=
.
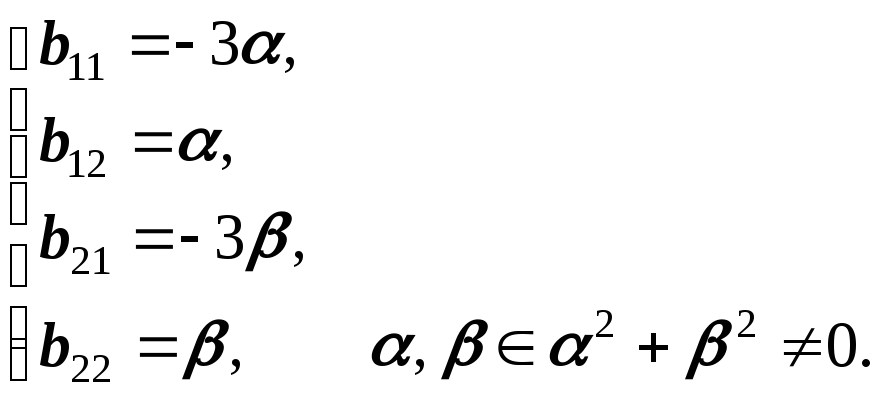Таким
образом, B=
где 2+2≠0,
являются левыми делителями нуля матрицы
А.
в)
Пусть B=
правый делитель нуля для A=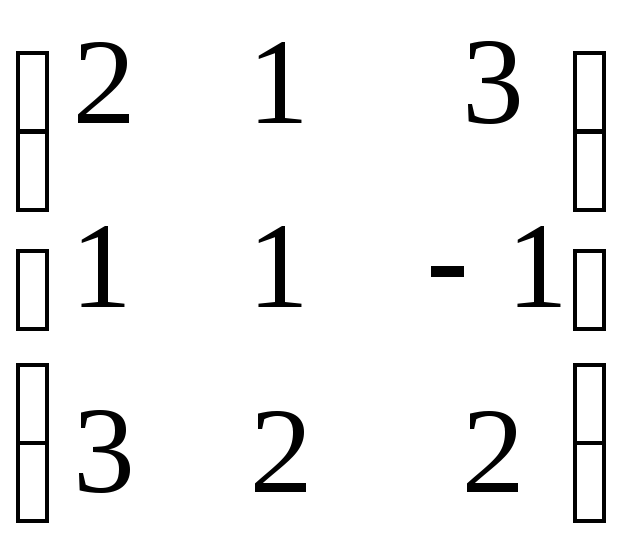
вM3(R),
то есть B≠O
и AB=O,
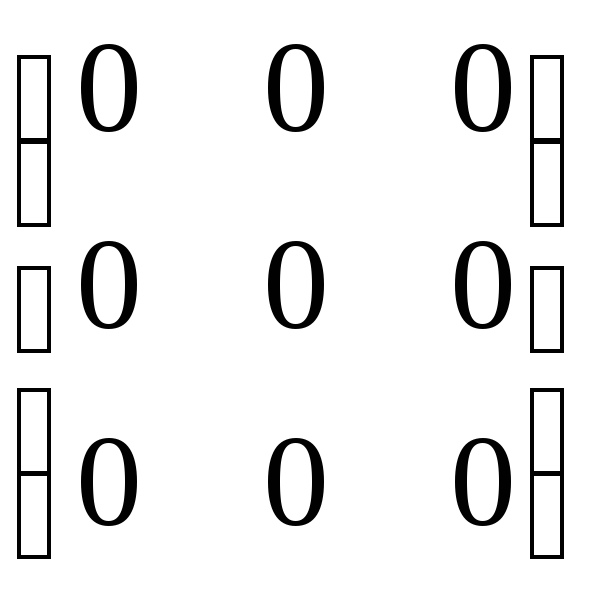
где O=
.
Имеем
AB=O
=
=
Применим к системе метод Гаусса. При этом заметим, что система состоит из трёх однотипных подсистем вида
Применяем к ней метод Гаусса:
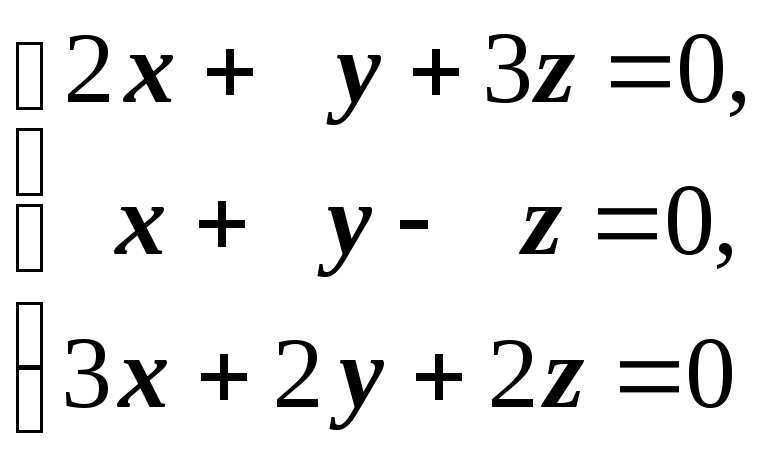
(1) Поменяли местами первое и второе уравнения системы. (2) Первое умножили на 2 и 3 и вычли соответственно из 2-го и 3-го
Положим z=. Тогда y=5 и x=y+z=5+=4, то есть
Это
означает, что первая подсистема системы
имеет решение 
вторая
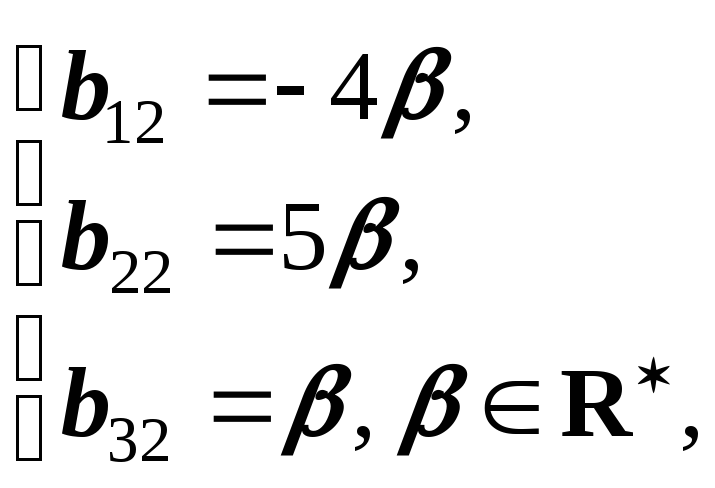третья
а решением всей системы является (4;
5;
;
4;
5;
;
4;
5;
),
.
Таким образом,B=
правые делители нуля для А
(
).
Пусть
теперь
левый делитель нуля для А.
Имеем
BA=O
=
=
Аналогично предыдущему, замечая, что система состоит из трёх однотипных подсистем вида
и применяя к ней метод Гаусса
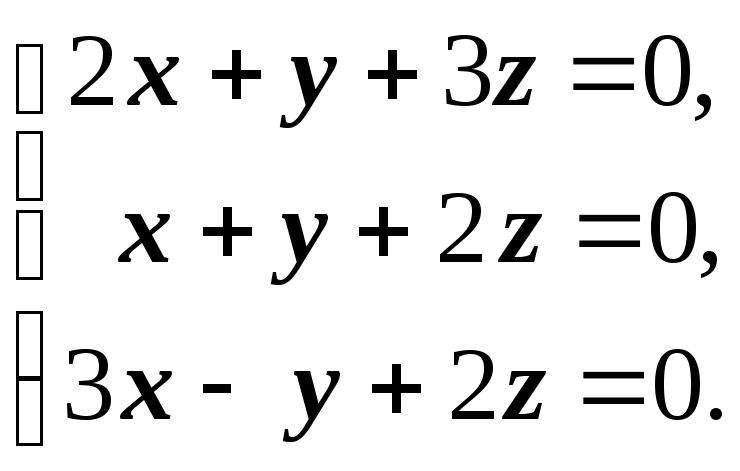
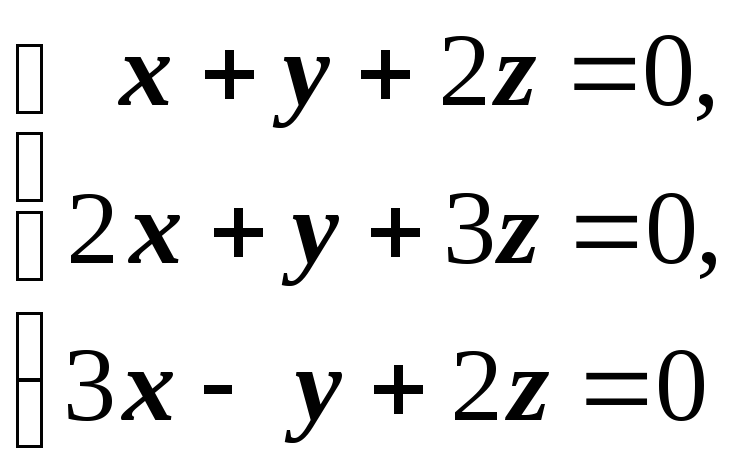
получаем
решение всей системы (;
;
;
;
;
;
;
;
),
.
СледовательноB=
левые делители нуля для (
).
Ответ:
а)
и
соответственно правые и левые делители
нуля матрицы А=
в кольцеM2(R)
(2+2≠0).
б)
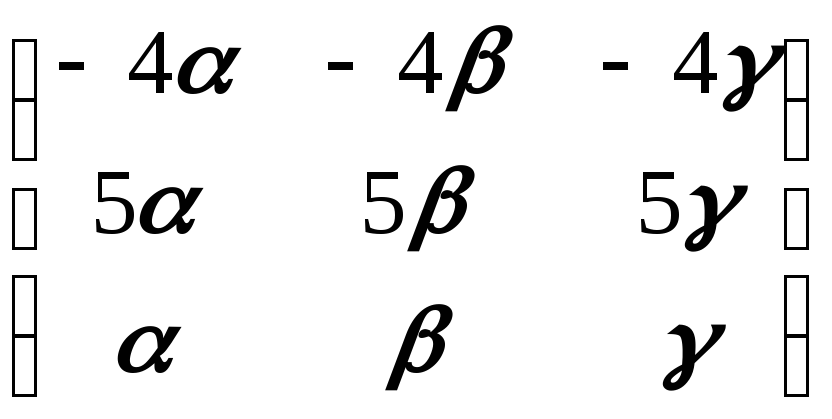и
соответственно правые и левые делители
нуля матрицы A=
в кольце
M3(R)
(
).
3.3.7. Доказать, что АMn(R) имеет делители нуля тогда, и только тогда, когда det A=0.