
Математика
.pdf
Основные формулы |
|
|
Определения |
|
|
и замечания |
|
|
|
|
|
13. Уравнение второй степени |
|
|
Уравнению (13) не удов- |
x2 + y2 + a2 = 0 , a ≠ 0 |
(13) |
летворяют никакие дей- |
|
не определяет никакой линии. |
|
|
ствительные значения x |
|
|
и y, и, следовательно, |
|
|
|
|
|
|
|
|
оно определяет пустое |
|
|
|
множество точек. |
Задачи |
|
|
|
Задача 1. Привести уравнения |
кривых второго порядка |
||
к каноническому виду. Построить соответствующие системы координат и кривые по их каноническим уравнениям.
а) 16x2 + 25y2 + 32x − 100y − 284 = 0; б) x2 −10x − 3y + 10 = 0.
Решение.
а) 16x2 + 25y2 + 32x − 100y − 284 = 0 – уравнение вида (2),
B = 0.
Преобразуем данное уравнение следующим образом:
(16x2 + 32x)+ (25y2 −100y)− 284 = 0; 16(x2 + 2x)+ 25(y2 − 4y)− 284 = 0;
16(x2 + 2x + 1− 1)+ 25(y2 − 4y + 4 − 4)− 284 = 0;
16(x + 1)2 −16 + 25(y − 2)2 − 100 − 284 = 0;
16(x + 1)2 + 25(y − 2)2 = 400;
(x + 1)2 + (y − 2)2 = 1.
25 16
151

Сделаем параллельный перенос осей координат. За новое начало координат примем точку O′(− 1; 2). Воспользуемся формулами (1) § 7:
x′ = x + 1, y′ = y − 2.
Каноническое уравнение принимает вид x′2 + y′2 = 1. 25 16
Таким образом, заданная кривая является эллипсом (рис. 1).
Рис. 1
б) x2 −10x − 3y + 10 = 0.
Решение.
Преобразуем данное уравнение следующим образом:
(x2 − 10x)− 3y + 10 = 0;
(x2 −10x + 25 − 25)− 3y + 10 = 0;
(x − 5)2 − 25 − 3y + 10 = 0;
(x − 5)2 = 3y + 15;
(x − 5)2 = 3(y + 5).
152

Сделаем параллельный перенос осей координат. За новое начало координат примем точку O′(5; − 5). Формулы параллель-
x′ = x − 5 |
|
ного переноса: |
. |
y′ = y + 5 |
|
Каноническое уравнение принимает вид x′2 = 3y′.
Таким образом, заданная кривая является параболой (рис. 2).
Рис. 2
Задача 2. Привести уравнение кривой второго порядка 4xy + 3y2 + 16x + 12y − 36 = 0 к каноническому виду. Построить
соответствующие системы координат и кривую по ее каноническому уравнению.
Решение.
Поскольку B = 4 ≠ 0, вначале выполним поворот системы
координат XOY |
на угол α. |
Поскольку |
A = 0, |
B = 4, C = 3, |
|||||||||
ctg 2α = |
A − C |
= − |
3 |
. |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
|
B |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ctg 2α |
|
− |
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
= − 3 |
|
|||
Отсюда cos 2α = |
|
= |
4 |
|
; |
||||||||
|
|
|
|
|
1 + ctg2 2α |
1 |
+ |
|
9 |
5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
16 |
|
|
|||
153

|
1+ cos 2α = |
1− |
3 |
|
|
|
|
|
1 ; |
||
cos α = |
5 |
= |
|||
|
2 |
2 |
|
|
5 |
|
1− cos 2α = |
1+ |
3 |
|
|
|
|
|
2 . |
||
sin α = |
5 |
= |
|||
|
2 |
2 |
|
|
5 |
Следовательно, α = arcsin 2 ; α ≈ 63°.
 5
5
Тогда формулы поворота системы координат дадут:
|
|
|
|
|
|
= x′ cos α − y′ sin α = |
|
1 |
x′ − |
|
2 |
y′, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x |
|
5 |
|
5 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y = x′ sin α + y′ cos α = |
x′ + |
|
y′. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя выражения x и y в данное уравнение, получим: |
|||||||||||||||||||||||||||||||
|
1 |
|
x′ |
− |
2 |
y′ |
|
|
2 |
x′ + |
1 |
|
y′ |
|
|
|
2 |
|
x′ + |
1 |
|
|
2 |
+ |
|
||||||
4 |
5 |
|
5 |
|
|
5 |
|
5 |
|
+ 3 |
|
|
|
5 |
y′ |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
x′ − |
2 |
y′ |
|
|
|
|
|
2 |
x′ + |
1 |
|
|
|
− 36 |
= 0 |
|
|
|
|
|||||||
|
+ 16 |
|
|
|
|
|
+ 12 |
|
|
|
|
|
y′ |
|
|
|
|
||||||||||||||
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x′ |
2 |
− |
4 |
y′x′ + |
1 |
x′y′ − |
2 |
y′ |
2 |
|
|
|
4 |
x′ |
2 |
+ |
4 |
x′y′ + |
1 |
y′ |
2 |
|
+ |
|||||||
4 |
|
5 |
5 |
5 |
|
|
+ 3 |
|
5 |
5 |
|
|
|||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+ 16 x′ − 32 y′ + 24 x′ + 12 y′ − 36 = 0. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
После раскрытия скобок и приведения подобных членов |
|||||||||||||||||||||||||||||||
получим 4x′2 − y′2 + 8 |
5x′ − 4 |
5y′ − 36 = 0 |
|
|
(*). |
|
|
|
|
|
|
|
|||||||||||||||||||
Таким |
|
образом, |
при |
повороте |
осей |
|
координат |
|
на |
угол |
|||||||||||||||||||||
α ≈ 63°, данное уравнение сводится к уравнению (*), т.е. к уравнению вида (2).
154
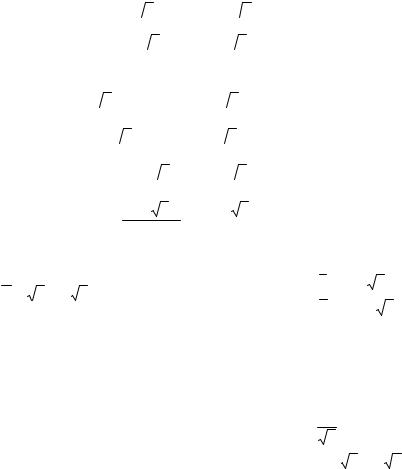
На втором этапе выполняем параллельный перенос системы координат.
Для этого сгруппируем члены с одноименными переменными:
(4x′2 + 8 5x′)+ (− y′2 − 4
5x′)+ (− y′2 − 4 5y′)− 36 = 0;
5y′)− 36 = 0;
4(x′2 + 2 5x′)− (y′2 + 4
5x′)− (y′2 + 4 5y′)− 36 = 0.
5y′)− 36 = 0.
Дополним полученные выражения до полных квадратов:
4(x′2 + 2 5x′ + 5 − 5)− (y′2 + 4
5x′ + 5 − 5)− (y′2 + 4 5y′ + 20 − 20)− 36 = 0; 4(x′ +
5y′ + 20 − 20)− 36 = 0; 4(x′ +  5)2 − 20 − (y′ + 2
5)2 − 20 − (y′ + 2 5)2 + 20 − 36 = 0;
5)2 + 20 − 36 = 0;
4(x′ +  5)2 − (y′ + 2
5)2 − (y′ + 2 5)2 = 36;
5)2 = 36;
|
|
|
|
|
|
|
(x′ + 5)2 |
− |
(y′ + 2 5)2 |
|
= 1. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь, |
поместив начало |
новой |
системы |
|
|
|
|
в |
точку |
|||||||||||||
X |
OY |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x′ + |
5 |
|
|
||||
O(− 5; − 2 |
5) и воспользовавшись формулами |
|
|
||||||||||||||||||||||
y = |
y′ + 2 |
|
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим каноническое уравнение |
х2 |
− |
у |
2 |
= 1 . |
|
|
|
|
|
|
|
|
|
|||||||||||
9 |
36 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Таким образом, заданная кривая – гипербола. |
|
|
|
|
|
X ′OY ′ |
||||||||||||||||
|
|
|
Построим все три системы |
координат: |
XOY , |
||||||||||||||||||||
и |
|
|
|
|
учитывая, что угол поворота |
α = arcsin |
2 |
|
(α ≈ 63°), |
||||||||||||||||
X |
OY , |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||
а точка |
|
в системе X ′OY ′ |
имеет координаты |
|
(− |
5; − 2 |
|
5) |
|||||||||||||||||
O |
|
|
|||||||||||||||||||||||
(рис. 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
155
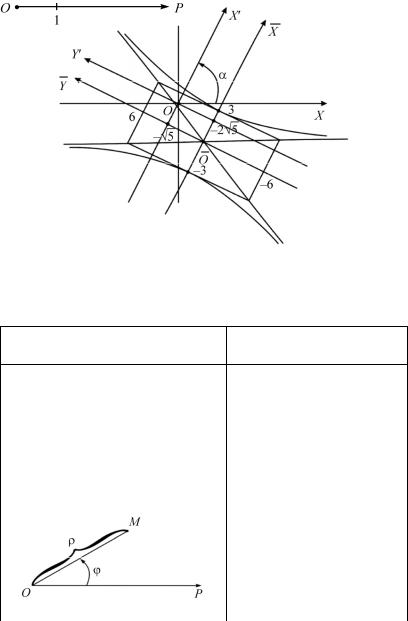
Рис. 3
§ 9. Полярные координаты
Основные формулы и рисунки |
Определения |
|
и замечания |
||
|
1. |
Полярная |
система |
коорди- |
|
|
нат определяется |
заданием |
||
Рис. 1 |
некоторой точки О (полю- |
|||
са), исходящего из этой |
||||
|
||||
|
точки луча (полярной оси) |
|||
|
и указанием единицы мас- |
|||
|
штаба (рис. 1). |
|
||
2. |
Полярными координатами |
|||
|
произвольной точки М на- |
|||
|
зываются |
числа |
ρ = OM |
|
|
и ϕ = POM (рис. 2). |
|||
|
ρ – полярный радиус; |
|||
Рис. 2 |
ϕ – полярный угол. |
|||
|
156 |
|
|
|

Основные формулы и рисунки |
Определения |
||||
и замечания |
|||||
|
|
||||
Задание точки М в полярной сис- Замечание 1. |
|
||||
теме координат – M (ρ; ϕ) . |
(1) Угол ϕ |
будем |
понимать |
||
|
|
так, как это принято в три- |
|||
|
|
гонометрии (т.е. углы, по- |
|||
|
|
лучаемые |
при |
вращении |
|
|
|
полярной оси вокруг полю- |
|||
|
|
са против часовой стрелки, |
|||
|
|
положительны; при враще- |
|||
|
|
нии полярной оси по часо- |
|||
|
|
вой стрелке – отрицатель- |
|||
|
|
ны). |
|
|
|
|
|
Замечание 2. |
|
||
|
|
Для того, чтобы соответст- |
|||
|
|
вие между точками плоско- |
|||
|
|
сти и парами чисел (ρ, ϕ) |
|||
было взаимнооднозначным, обычно считают, что
0 ≤ ρ < ∞ и 0 ≤ ϕ < 2π (или − π < ϕ ≤ π ).
Замечание 3.
На практике пользуются системой полярных координат, в которой радиус ρ может принимать и отрицательные значения.
Следует запомнить, что система полярных координат, в которой полярный радиус ρ может принимать любые значения (положи-
157
Основные формулы и рисунки |
|
Определения |
|
||||||||
|
и замечания |
|
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
тельные, |
|
отрицательные |
|||
|
|
|
|
|
|
и равные нулю), называется |
|||||
|
|
|
|
|
|
обобщенной |
системой |
по- |
|||
|
|
|
|
|
|
лярных координат. |
|
||||
3. |
|
|
|
|
|
Если полюс полярной сис- |
|||||
|
|
|
|
|
|
темы координат |
находится |
||||
|
|
|
|
|
|
в |
начале |
|
прямоугольной |
||
|
|
|
|
|
|
системы координат, а по- |
|||||
|
|
|
|
|
|
ложительная |
полуось |
OX |
|||
|
|
|
|
|
|
совпадает с полярной осью, |
|||||
|
|
|
|
|
|
ось же OY перпендикуляр- |
|||||
|
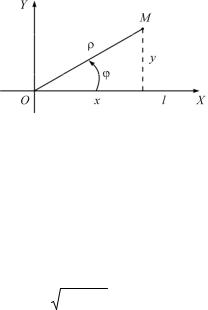
Рис. 3 |
|
|
|
|
на |
оси OX |
и |
направлена |
||
|
|
|
|
|
так, что |
ей |
соответствует |
||||
|
|
|
|
|
|
||||||
|
x = ρ cos ϕ, |
(2) |
полярный |
угол |
π |
то |
|||||
|
|
|
|
|
ϕ = 2 , |
||||||
|
y = ρ sin |
ϕ. |
|
по |
известным |
полярным |
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
координатам точки ее пря- |
|||||
|
|
|
|
|
|
моугольные координаты x, |
|||||
|
|
|
|
|
|
y вычисляются по форму- |
|||||
|
|
|
|
|
|
лам (2) (рис. 3). |
|
|
|||
4. ρ = |
x2 + y2 , tg ϕ = |
y |
|
Если известны прямоуголь- |
|||||||
|
. |
(3) |
ные координаты x и y точ- |
||||||||
x |
|||||||||||
|
|
|
|
|
|
ки, ее полярные координа- |
|||||
|
|
|
|
|
|
ты определяются по фор- |
|||||
|
|
|
|
|
|
мулам (3). |
|
|
|
|
|
5. Уравнение линии |
в полярной |
|
|
|
|
|
|
||||
системе |
координат |
ρ = ρ(ϕ) |
или |
|
|
|
|
|
|
||
F (ρ,ϕ)= 0 . |
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
158
Задачи
|
|
|
π |
|
π |
|
3π |
||
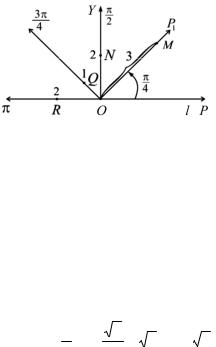
Задача 1. Построить точки |
M |
3; |
|
, |
Ν 2; |
, |
Q 1; |
|
, |
|
|
||||||||
|
|
|
4 |
|
|
2 |
|
4 |
|
R(2; π) в полярной системе координат. |
|
|
|
|
|
|
|
||
Решение. |
|
|
|
|
|
|
|
|
|
Проведем через полюс О ось OP1 |
, под углом π к полярной |
||||||||
|
|
|
|
|
|
4 |
|
|
|
оси OP (положительное направление указано стрелкой) и отложим от полюса в положительном направлении оси ΟΡ1 отрезок
ОМ, равный трем единицам масштаба. Конец М этого отрезка и будет искомой точкой (рис. 4).
Аналогично строятся точки N, Q, R.
Рис. 4
Задача 2. Найти прямоугольные координаты точки А, по-
|
π |
лярные координаты которой 2; |
. |
|
4 |
Решение. |
|
По формулам (2) x = ρ cos ϕ, |
|
y = ρ sin ϕ |
|
получаем: |
|
x = 2 cos π = 2 |
2 = 2 , x = 2, |
4 |
2 |
159
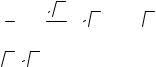
y = 2 sin π = 2  2 =
2 =  2 , y =
2 , y =  2 . 4 2
2 . 4 2
Следовательно, A( 2;
2;  2 ).
2 ).
Задача 3. Дано уравнение кривой ρ = a(1 + cosϕ) в поляр-
ных координатах. Требуется построить эту кривую по ее полярному уравнению.
Решение.
Построим линию ρ = a(1+ cos ϕ), где a > 0.
Будем давать значения полярному углу ϕ от ϕ = 0 до
ϕ = 2π через промежуток α = π и вычислим соответствующие
8
значения ρ. Найденные значения поместим в таблицу. Примем
произвольный отрезок за единицу масштаба, которой мы будем пользоваться при построении ρ. По значениям ρ и ϕ из табли-
цы построим точки, соответствующие |
каждой |
паре чисел ρ |
|||||||||||||||||||||||||
и ϕ, |
и соединим их плавной кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ϕ |
0 |
|
|
π |
|
π |
|
3π |
|
|
π |
|
|
5π |
|
|
|
3π |
|
|
7π |
|
|||||
|
8 |
|
4 |
|
8 |
|
2 |
|
|
8 |
|
4 |
|
|
8 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ρ |
|
2a |
1,92a |
1,71а |
1,38а |
|
а |
|
0,62а |
0,29а |
0,08а |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
π |
|
9π |
|
|
5π |
|
11π |
|
3π |
13π |
|
|
7π |
15π |
|
2π |
|||||||||||
|
8 |
|
|
4 |
|
|
8 |
|
|
2 |
|
|
8 |
|
|
|
4 |
|
|
8 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 |
0,08а |
0,29а |
0,62а |
|
а |
1,38а |
|
1,71а |
1,92а |
|
2а |
||||||||||||||||
Ввиду четности функций кривая симметрична относительно полярной оси (рис. 5).
160
