Лабораторная работа № 8 определение вязкости воздуха по истечению из капилляра

Цель работы: измерить коэффициент динамической вязкости воздуха.

Приборы и принадлежности: ЛКТ-9: электрочайник, соединительные шланги, груша-помпа с зажимом, капилляр; термометр, баллон с двумя штуцерами.

Краткие теоретические сведения

П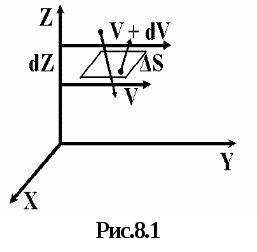ри движении жидкости или газа между ее (его) соседними слоями, движущимися с разными скоростями, возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоев. Возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному слою некоторое количество движения (импульс), вследствие чего он начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, что приводит к торможению быстрого слоя. При переносе импульса от слоя к слою происходит изменение импульса всех слоев. Это значит, что на каждый из слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона).

Рассмотрим жидкость, движущуюся в направлении оси y (рис.8.1).

1) Пусть на расстоянии dz скорости потока отличаются на величину dv. Отношение dv/dz характеризует изменение скорости потока в направлении оси z и называется градиентом скорости. Таким образом, градиент скорости численно равен изменению скорости на единице длины в направлении, перпендикулярном скорости.

Согласно закону Ньютона, сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения S и градиенту скорости:

. (8.1)

Величина  («эта») называется коэффициентом внутреннего трения, или коэффициентом динамической вязкости. Если в формуле (8.1) положить численно dv/dz = 1 и S = 1, то F =  , т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на единичной поверхности соприкосновения двух слоев, движущихся друг относительно друга с градиентом скорости, равным единице. B системе СИ единица измерения вязкости ] = кг/мс или (Пас).

Коэффициент вязкости  зависит от природы жидкости (или газа) и для данной жидкости с повышением температуры уменьшается, а для газа с повышением температуры увеличивается, например:

• для воды (10C) = 1,31 мПас, (50C) = 1,00 мПас, (90C) = 0,32 мПас;

• для воздуха (0C) = 17,2 мкПас, (20C) = 18,2 мкПас.

Наряду с коэффициентом динамической вязкости  часто используют коэффициент кинематической вязкости

, (8.2)

где - плотность жидкости.

Описание метода

Накачаем в баллон объемом V₀ газ и будем «стравливать» его в атмосферу через капилляр диаметром d и длиной L. Если разность давления Р внутри сосуда и атмосферного давления Р₀ достаточно мала, (Р–Р₀) << Р₀, и течение газа в капилляре ламинарное (слоистое), то расход газа определяется через его вязкость η, перепад давлений на концах капилляра, геометрическими размерами капилляра и описывается формулой Пуазейля:

а падение давления в баллоне описывается изотермическим процессом с убывающей массой газа:

При небольших перепадах давления можно заменить Р на среднее за время наблюдения значение давления газа в баллоне  Р , а V = V₀ . В результате получим

,

откуда следует, что перепад давлений: ΔP = P – P₀ убывает по экспоненте с постоянной времени :

.

Коэффициент пропорциональности на графике зависимости 1n(ΔР) от времени даст значение τ, по которому можно найти вязкость:

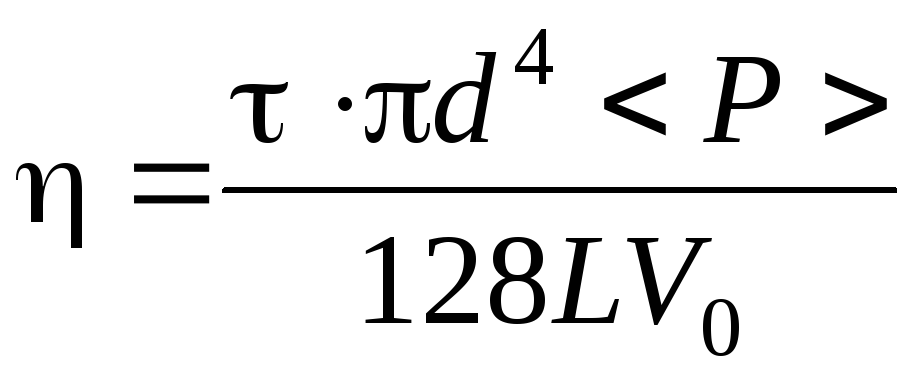. (8.3)

Если температура T газа в капилляре отличается от температуры Т₀ газа в баллоне, то объем прошедшего через капилляр газа равен и расчетная формула для вязкости

. (8.4)

При больших значениях ΔР течение газа будет турбулентным (при поступательном движении происходит перемешивание слоев газа). Зависимость 1n(ΔР) от времени также оказывается линейной, но с меньшим наклоном. По излому графика можно опознать изменение типа течения. Критерием типа течения является значение числа Рейнольдса

,

где r - радиус капилляра, v - средняя скорость газа, ρ- плотность газа (при нормальных условиях ρ_возд = 1,3 кг/м³). Течение в трубе ламинарное при Re  1000. Поскольку имеем

.

При d = 0,28 мм и L = 30 мм получим Re ~ 1000 при ΔP ~ 100÷150 мм рт.ст. Эта оценка показывает, что течение воздуха в капилляре будет ламинарным при избыточном давлении в баллоне в несколько десятков мм рт.ст. Тогда в формулах (8.3) и (8.4) можно принять в качестве P значение давления на 40 – 60 мм рт.ст. больше атмосферного, т.е. P = 800 мм рт.ст. А критическое значение числа Рейнольдса:

. (8.5)

Критическое давление определяется в эксперименте по излому графика как давление в точке, находящейся левее пересечения прямых для турбулентного и ламинарного режимов истечения воздуха из капилляра (см. рис.8.2).