2.3. Показатели надежности объекта

Показатель надежности  это количественная характеристика одного или нескольких свойств, составляющих надежность объекта. Различают единичные и комплексные показатели надежности.

Единичный показатель характеризует одно из свойств надежности объекта. К единичным показателям относятся показатели безотказности, долговечности, ремонтопригодности и сохраняемости. В технической диагностике используются в основном показатели безотказности и ремонтопригодности. Поэтому рассмотрим именно эти показатели надежности.

Безотказность объекта характеризуют следующие показатели:

• вероятность безотказной работы;

• средняя наработка до отказа;

• средняя наработка на отказ;

• интенсивность отказов;

• параметр потока отказов.

Основные показатели ремонтопригодности:

• вероятность восстановления;

• среднее время восстановления;

• интенсивность восстановления.

Комплексный показатель надежности характеризует несколько свойств, составляющих надежность объекта. К основным комплексным показателям относятся коэффициенты готовности, оперативной готовности, коэффициент простоя, коэффициент технического использования.

Рассмотрим указанные показатели надежности более подробно.

Вероятность безотказной работы  это вероятность того, что в пределах заданной наработки отказ объекта не возникает, т. е. время T безотказной работы объекта будет больше времени функционирования t:

. (2.5)

Величина Т является случайной: любой из объектов данного типа отказывает в произвольный, заранее неизвестный момент времени. Для очень большой совокупности объектов существует закономерность, при которой с вероятностью Р(t) любой из объектов проработает безотказно время Т, большее, чем заданное. В этом заключается математический смысл данного показателя безотказности.

Статистически значение Р(t) оценивается отношением числа объектов, продолжающих после истечения времени t безотказно работать, к общему числу N объектов, работоспособных в момент времени t = 0:

, (2.6)

где  статистическая оценка вероятности безотказной работы; n (t) - число объектов, отказавших за время t. Формула (2.6) применяется для оценки надежности невосстанавливаемых объектов, и основным условием получения достоверной оценки является накопление большого числа опытных данных. В соответствии с законом больших чисел по мере увеличения числа испытуемых объектов N статистические показатели надежности, в данном случае , становятся все менее случайными и, таким образом, все точнее оценивают неизвестные значения вероятностных показателей, в данном случаеР(t).

Из определения вероятности безотказной работы следует, что этот показатель надежности является функцией времени, обладающей следующими свойствами: 1) Р(t)  убывающая функция времени; 2) ; 3)Р(0) = 1, .

Вероятность безотказной работы изделия в целом, состоящего из последовательно соединенных узлов, сборочных единиц, определяют по формуле

, (2.7)

где P_j(t)  вероятность безотказной работы за время j-го узла; k  число узлов структурной схемы надежности.

Наряду с безотказной работой используется противоположное событие  отказ, при этом вероятность отказа объекта Q (t) определяется соотношением

(2.8)

Функция Q (t) представляет собой при функцию распределения случайной величиныТ. Статистические значения Q(t) оцениваются отношением числа объектов, отказавших за время t, к общему числу объектов, работоспособных в момент t = 0:

(2.9)

Показатели безотказности, полученные в различных условиях испытаний или эксплуатации, различаются по величине. Поэтому должны оговариваться или стандартизироваться не только значения показателей, но и условия, для которых они заданы или при которых они получены.

Показатели безотказности, например, для промышленных приборов и средств автоматизации рекомендуется устанавливать при следующих условиях:

• температура окружающего воздуха ………………..25+10⁰С;

• относительная влажность……………………………45…80%;

• барометрическое давление ………………………….630…800 мм рт. ст.;

• отклонение напряжения питания……………………от +10 до –15%;

• частота переменного тока (питания)………………...50±1 Гц, 400±12Гц;

• внешние воздействия……………………………….….в пределах норм,

оговоренных ТУ.

Для дифференцируемой функции Q(t) можно получить плотность распределения времени (дифференциальный закон распределения):

(2.10)

где f(t)  плотность распределения времени безотказной работы объекта. Статистически f(t) определяется отношением числа отказавших в единицу времени объектов к количеству работоспособных объектов в момент времени t=0:

(2.11)

где  количество объектов, отказавших к моменту времени

Частотой отказов называется отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что все вышедшие из строя изделия не восстанавливаются.

Согласно определению частота отказов

, (2.12)

где n(t) – число отказавших образцов в интервале времени от t – t/2 до t + t/2.

Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому

. (2.13)

Частота отказов  величина положительная, так как Q(t) – неубывающая функция. Площадь, ограниченная кривой частоты отказов, равна единице, потому что

.

Конкретный вид кривой может быть различным для разных видов аппаратуры.

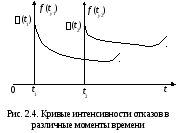
Типичный, часто встречающийся вид кривой частоты отказов показан на рис. 2.3. Кривая имеет три явно выраженных участка.

Первый участок – это так назы­ва­емый более или менее короткий период приработки аппаратуры. Не­посредственно после включения из­го­тов­ленной аппаратуры проявляются скры­тые дефекты производства, не об­на­ру­женные техническим контролем. Час­тота отказов на первом участке велика, но постепенно снижается, так как большая часть дефектов обнаруживается после начала эксплуатации.

Второй участок соответствует длительному периоду времени нормальной эксплуатации аппаратуры. Частота отказов здесь невелика и медленно снижается и обусловлена в основном нарушениями правил эксплуатации и внезапными перегрузками.

Третий участок – период аварийных отказов соответствует периоду старения и износа аппаратуры; из-за изменения (ухода) внутренних параметров устройства частота отказов повышается. В этот период в основном имеют место постепенные отказы, возникающие вследствие накопления ухудшений физико-химических свойств объекта. В конце третьего участка частота отказов снова снижается, так как вероятность безотказной работы к этому времени очень мала.

Долговечность системы определяется началом периода аварийных отказов. Практический интерес представляет рассмотрение «жизни» системы на интервалах времени, не превышающих ее долговечность. При этом, если на предприятии-изготовителе производится предварительная приработки, а период эксплуатации отсчитывается от момента поступления к потребителю, то эксплуатационный ресурс еще уменьшается.

В связи с постоянным повышением качества аппаратуры, особенно радиоэлектронной, длительность второго участка кривой для многих изделий увеличивается. Практически за все время эксплуатации до морального старения аппаратура не успевает выйти на третий участок.

Для основных элементов систем электроснабжения период приработки длится до 3…5 лет. Процессы старения и износа проявляются для воздушных линий (ВЛ) на опорах из пропитанной древесины через 15…20 лет после ввода в эксплуатацию, для трансформаторов и КЛ – через 20…30 лет (в первую очередь за счет старения изоляции). Старение и износ коммутационной аппаратуры наступает через 40…50 лет. Обычно эта аппаратура морально устаревает раньше, нежели физически. В основном элементы СЭС высоконадежны. Время их безотказной работы значительно превышает время восстановления.

Интенсивность отказов λ(t) с позиций теории вероятностей вводится следующим образом (рис. 2.4). Предположим, что устройство исправно проработало в течение времени t₁. Очевидно, что время его дальнейшей работы до отказа τ_у1 есть случайная величина, имеющая свою плотность распределения f(t_у1).Эта плотность, вычисленная в момент времени t = t₁, обозначается λ(t₁).

Далее предположим, что устройство проработало время t₂ , повторим рассуждения и вычислим λ(t₂). Меняя время t от 0 до , можно таким образом построить плавную кривую интенсивности отказа λ(t) (см. рис. 2.3).

Интенсивность отказов определяется по формуле:

(2.14)

т.е. интенсивность отказов представляет собой условную плотность распределения времени безотказной работы в момент времени t при условии, что до этого момента времени отказ не наступил.

Статистически интенсивность отказов в момент времени t определяется отношением числа отказавших в единицу времени объектов к числуработоспособных объектов в момент времениt:

, (2.15)

где величина представляет собой число объектовN_p(t), работоспособных в момент времени t; N_p(t) = (N_i+N_i+1)/2; N_i – число изделий, исправно работающих в начале интервала (t); N_i+1  число изделий, исправно работающих в конце интервала.

Формула (2.15) есть статистическое определение интенсивности отказов. Вероятностная оценка этой характеристики находится из выражения

λ(t) = a(t)/P(t). (2.15')

Представим соотношение (2.14) в виде и проинтегрируем его в пределах от 0 доt:

.

Учитывая, что табличный интеграл , получаем:; отсюда следует, что

(2.16)

Формула (2.16) устанавливает связь между вероятностью безотказной работы за время t и интенсивностью отказов и отражает тот факт, что при любом характере изменения величинаР(t) будет тем меньше, чем больше значение . Это выражение иногда называютобщим законом надежности, который применим для любых потоков отказов невосстанавливаемых объектов.

П

ри расчете вероятности безотказной работы по-характеристикам среднее квадратическое отклонение равно:

• для i-ой детали ;

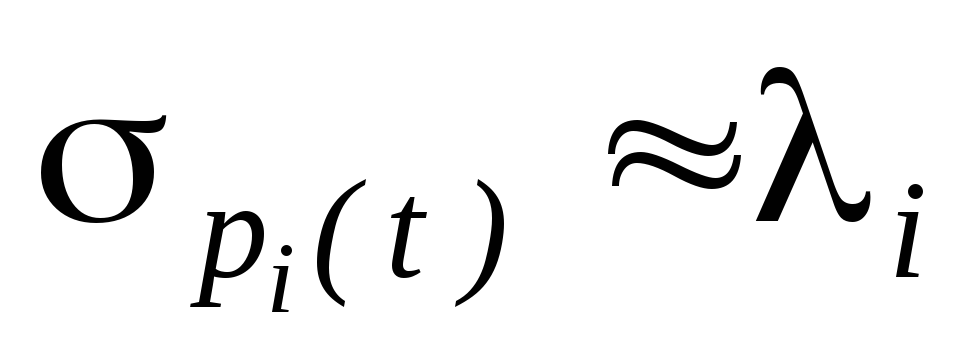• для j-ой сборочной единицы ; (2.17)

• для изделия в целом .

При отсутствии данных о надежности элементов в фактических условиях хранения, транспортирования  принимает следующие соотношения пересчета интенсивности отказов

_хр=10^–3_р, _р.тр=1,5_р , _хр.тр=_хр,

где _р, _хр, _тр – интенсивность отказов элемента соответственно при работе, хранении и транспортировании.

Пример 2.2. Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ₁ = 0,16∙10^–3 1/ч = const. Интенсивности отказов двух электромеханических устройств нелинейно зависят от времени и определяются следующими формулами:

λ₂ = 0,223∙10^-4 t 1/ч, λ₃ = 0,06∙10^-6 t^2,6 1/ч .

Необходимо рассчитать вероятность безотказной работы изделия в течение 100 часов.

Решение. На основании формулы (2.16) имеем

.

.

Для t = 100 ч

.

Пример 2.3. На испытание поставлено N = 400 изделий. За время t = 3000 ч отказало n(t) = 200 изделий, за интервал времени ∆t = 100 ч отказало n(∆t) = 100. Требуется определить Р*(3000), Р*(3100), Р*(3050), а*, λ*.

Решение. 1. По формуле (2.6) найдем вероятность безотказной работы:

Для t_н = 3000 ч (начало интервала)

;

для t_к = 3100 ч (конец интервала)

.

Определим среднее число исправно работающих изделий в интервале ∆t:

.

Число отказавших изделий за время t = 3050 ч

n(3050) = N–N_р = 400–150 = 250,

тогда

.

2. По формуле (2.12) определяем частоту отказа:

1/ч.

3. По формуле (2.15) определяем интенсивность отказа

1/ч.

Интенсивность отказа можно также определить по формуле (2.15'):

1/ч.

Средняя наработка до отказа  это математическое ожидание наработки объекта до первого отказа. Средняя наработка до отказа Т₁ определяется по формуле:

Интегрируя это выражение по частям, получим:

Практически во всех случаях член обращается в нуль, так как имеет место соотношение, следующее из того, что срок службы любого объекта ограничен, и потомуР(t) быстрее стремится к нулю, чем . Таким образом, получаем

(2.18)

т.е. средняя наработка до отказа численно равна площади под кривой P(t).

Статистическая средняя наработка до отказа группы однотипных объектов определяется как отношение суммарного значения наработки каждого из них до появления отказа к общему числу объектов N, работоспособных в момент t = 0

(2.19)

где t_i  наработка до отказа i-го объекта.

Имея данные о количестве вышедших из строя элементов n_i в каждом i-м интервале времени, среднюю наработку до отказа лучше определять из уравнения

. (2.19,а)

В выражении (2.19а) t_{ср i} и m находятся по следующим формулам:

t_{ср i} = (t_i–1+t_i) / 2, m = t_k / ∆t,

где t_i–1 – время начала i-го интервала; t_i – время конца i-го интервала; ; t_k – время, в течение которого вышли из строя все элементы; ∆t = t_i–1– t_i – интервал времени.

Так как практически невозможно осуществить испытания всех элементов до отказа, то в первом приближении при большом числе N среднюю наработку до отказа можно определить зависимостью

, (2.19,б)

где N – число элементов, поставленных на испытания; m – число отказавших элементов; t  время испытания.

Формула (2.19,б) справедлива при числе m отказавших элементов, близких к N.

Пример 2.4. На испытания поставлено N = 10 невосстанавливаемых элементов. Испытания проводились в течение времени t = 100 ч. В процессе проведения испытаний отказало 8 элементов, при этом отказы зафиксированы в следующие моменты времени: t₁ = 20 ч, t₂ = 30 ч, t₃ = 50 ч, t₄ = 30 ч, t₅ = 40 ч, t₆ = 60 ч, t₇ = 70 ч, t₈ = 60 ч. Оставшиеся два элемента не отказали. Определить среднюю наработку до отказа.

Решение. Вычислим наработку до отказа для невосстанавливаемого элемента по формуле (2.19,б)

.

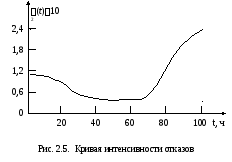
Пример 2.5. Найти интенсивность отказов λ(t) и построить график изменения кривой интенсивности отказов по данным, представленным в табл. 2.1. На испытания поставлено N = 100 элементов, испытания проводились в течение времени t = 100 ч.

Для построения кривой интенсивности отказов (рис. 2.5) воспользуемся формулой (2.15):

. .

Таблица 2.1

Исходные данные результатов испытаний

Интервал времени,	Число отказов в интервале, n()	Число N(ti) работоспособных элементов к моменту времениti		n()	Nр(ti)
0 … 10 10… 20 20 … 30 30 … 40 40 … 50	10 9 6 2 2	90 81 75 73 71	50 … 60 60 … 70 70 … 80 80 … 90 90… 100	3 2 5 9 10	68 66 61 52 42

. .

. .

. .

. .

Пример 2.6. Система состоит из N = 12600 элементов, средняя интенсивность отказов которых λ_ср = 0,32∙10^-6 1/ч. Необходимо определить вероятность безотказной работы в течение 50 ч и вычислить среднюю наработку до первого отказа.

Решение. Интенсивность отказов системы определяют по формуле λ_с = λ_cр∙N = 0,32∙10^-6∙12600 = 4,032∙10^-3 1/ч. Тогда на основании (2.16) получаем

≈0,82

и среднюю наработку до отказа .

Средняя наработка на отказ (среднее время безотказной работы)  отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. В соответствии с определением средняя наработка на отказ Т₀ задается формулой:

(2.20)

где t  суммарная наработка; r(t)  число отказов, наступивших в течение времени наработки t;  математическое ожидание этого числа отказов.

Статистическая оценка средней наработки на отказ вычисляется по формуле:

. (2.21)

Если на испытании находится N образцов в течение времени t, то наработка на отказ вычисляется по формуле:

, (2.21,a)

где t_ij  время исправной работы j-го образца изделия между (i1) и i-м отказами; n_j – число отказов за время работы t_j-го образца.

Если в процессе испытаний или эксплуатации в качестве статистической оценки получена средняя наработка на отказ, то вероятность безотказной работы элемента за время t равна:

,(2.22)

где t_p  время работы, t_хр  время хранения. Например, устройство работает 10 ч, а общее время работы изделия 50 ч. Следовательно, время хранения составит 40 ч.

Пример 2.8. При испытаниях некоторого устройства, имеющего время работы до отказа, распределенное по нормальному закону, получено 10 реализаций наработки до отказа (в часах): 120, 110, 80,130, 120, 140, 80, 150, 130, 140. Требуется найти доверительные границы с доверительной вероятностью 0,95 для средней наработки на отказ и дисперсии Д_х.

Решение. Имеем ч, ч², ч.

По формулам (1.22) и (1.23) определим границы средней наработки на отказ

.

Согласно табл. П1 имеем . Отсюда дляt_ср получаем значения нижней и верхней границы средней наработки на отказ соответственно 105,4 ч и 134,6 ч. Вычисления доверительного интервала для дисперсии ведется по формуле (1.24). Имеем N = 10, S² = 576 ч, (0,95; 9) = 16,92,(0,05; 9) = 3,33 (см. табл. П.2). Тогда доверительный интервал для дисперсии составит 430 ч и 1735 ч.

Параметр потока отказов  отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку к значению этой наработки. Параметр потока отказов определяется по формуле:

, (2.23)

где  числа отказов к моментам времени иt соответственно.

Статистическая оценка параметра потока отказов определяется по формуле:

(2.24)

где r (t₂), r (t₁)  числа отказов к моментам времени t₂ и t₁ соответственно.

Для простейшего потока отказов, т.е. для потока, обладающего свойством стационарности, ординарности и отсутствия последствия, параметр потока отказов совпадает с интенсивностью отказов, т.е.

const .

Рассмотрим показатели ремонтопригодности.

Вероятность восстановления  это вероятность того, что время восстановления работоспособного состояния объекта не превысит заданного значенияt. По определению

(2.25)

где Р_В (t)  вероятность восстановления объекта.

Время восстановления  это то время, которое затрачивается на обнаружение, поиск места отказа и устранение последствий отказа. Вероятность восстановления представляет собой функцию распределения времени восстановления объекта, т.е. интегральный закон распределения времени восстановления, а производная по функции Р_В (t) по времени дает плотность распределения случайной величины f_B(t) (дифференциальный закон распределения) времени восстановления

Интенсивность восстановления  условная плотность вероятности восстановления работоспособного состояния объекта, определенная для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено. Интенсивность восстановления определяется по формуле:

(2.26)

Интегрируя соотношение (2.26) в пределах (0, t), получаем

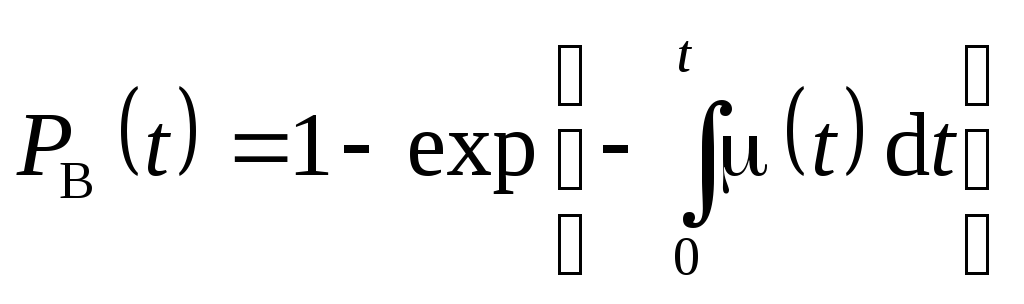. (2.27)

Полученное выражение устанавливает связь между интенсивностью и вероятностью восстановления для любых законов распределения времени восстановления.

Статистическая оценка интенсивности восстановления имеет вид:

, (2.28)

где n (t),  числа объектов, для которых восстановление закончилось к моментам времени t, ; N_B(t)  число объектов, ожидающих восстановления к началу промежутка времени .

Среднее время восстановления (Т_В)  это математическое ожидание времени восстановления (Т_В) работоспособного состояния объекта после отказа:

(2.29)

Для случая, когда процесс восстановления рассматривается как простейший , имеет место равенство:

. (2.30)

Статистическая оценка среднего времени восстановления задается формулой

, (2.31)

где t_Bi  время восстановления i-го объекта; n_B  число восстановленных объектов.

В случае усеченной выборки, когда в результате испытаний объектов получены r возрастающих значений наработки (r  n) t₁, t₂, …, t_r, а n – r объектов по истечении некоторого времени остались исправными, параметрыT и  можно оценить по методу квантилей следующим образом.

Считаем, что за время t_i вероятность выхода из строя испытываемых N объектов составляет P_i = i/N. Для этой вероятности по табл. П.5 определяем квантили u_p и составляем r уравнений:

T+u_p1 = t₁ ,

T+u_p2 = t₂ , (2.32)

……….……..

T+u_pr = t_r .

Полученную систему уравнений решаем по методу наименьших квадратов. Для чего умножим левую и правую части каждого из уравнений системы на u_p1, u_p2,…, u_pr соответственно и все r уравнений сложим. В результате получим первое так называемое нормальное уравнение

. (2.33)

Второе нормальное уравнение получим суммированием уравнений системы (2.32):

, (2.34)

Уравнения (2.33) и (2.34) решаем относительно неизвестных T и  и находим таким образом их оценки.

Точность полученных значений T и  может быть оценена с помощью уравнений

, , (2.35)

где k = (T – t₀)/; f₂ (k) и f₃ (k) – вспомогательные функции, определяемые по табл. П.6.

Пример 2.9. Испытания 100 ламп накаливания продолжались t₀=500 ч. За время испытаний вышло из строя 5 ламп с наработкой до отказа в часах соответственно t₁ = 50, t₂ = 150, t₃ = 250, t₄ = 300, t₅ = 450. Определить среднюю наработку до отказа ламп и среднее квадратическое отклонение, полагая, что срок службы ламп подчиняется нормальному закону.

Решение. Для вероятностей 0,01; 0,02; 0,03; 0,04; 0,05 по табл. П.5 находим квантили :

; ;;.

Составляем уравнения:

T – 2,33σ = 50,

T – 2,05σ = 150,

T – 1,88σ = 250,

T – 1,75σ = 300,

T – 1,64σ = 450.

Для решения данной системы уравнений складываем их и получаем

5T – 9,65 σ = 1200.

Затем, умножая исходные уравнения на коэффициенты при σ и суммируя, получаем

9,65T – 18,90 σ = 2160.

Решая нормальные уравнения, находим Т1315 ч, σ = 557 ч.

Для оценки точности полученных значений иопределяем

.

По табл. П.6 находим f₂ (1,46) = 33, 34; f₃(1,46) = 11,55. Тогда

.

Откуда ч,ч.

Как видно, точность определения параметров распределения в условиях данного примера невысокая. Доверительные интервалы величиной ±2σ, что соответствует вероятности приблизительно 95%, в данном случае составляют

ч , ч.

В табл. 2.4 приведены расчетные значения показателей надежности основных элементов СЭС и их условные обозначения. Данные носят ориентировочный характер.

Таблица 2.4

Расчетные значения показателей надежности элементов СЭС

Элемент	Условное обозначе- ние на схемах	Интенсив-ность отказов λ, год–1	Среднее время восстановления Тв, ч	Интенсив-ность пред­намеренных отключений ν, год–1	Среднее время обслу-живания Тоб, ч
Воздушная линия 35, 110 кВ одноцепная, на 1 км длины	Л	0,08	8	0,15	8
Воздушная линия 35, 110 кВ двухцепная, на 1 км длины	2Л	0,008	10	0,01	8
Воздушная линия 6, 10 кВ одноцепная, на 1 км длины	Л	0,25	6	0,25	5,8
Кабельная линия 6,10 кВ, на 1 км длины	К	0,10	25	0,5	3
Две кабельные линии в одной траншее, на 1 км длины	2К	0,05	15	0,05	3
Воздушная линия 0,38 кВ, на 1 км длины	Л	0,20	4	0,3	5
Трансформатор с высшим напряжением 35, 110 кВ	Т	0,03	30	0,5	12
Трансформатор с высшим напряжением 6, 10 кВ	Т	0,035	8	0,3	8
Ячейка выключателя 35, 110 кВ	Q	0,02	7	0,3	6
Продолжение таблицы 2.4
Ячейка выключателя 6, 10 кВ внутренней установки	Q	0,015	6	0,2	6
Ячейка выключателя 6, 10 кВ КРУН наружной установки	Q	0,05	5	0,3	5
Ячейка отделителя (ОД) или короткозамыкателя (КЗ) 35,110 кВ	QR, QK	0,05	4	0,3	5
Ячейка разъединителя 35, 110 кВ	QS	0,005	4	0,25	4
Ячейка разъединителя 6, 10 кВ внутренней установки	QS	0,002	3	0,2	3,5
Ячейка разъединителя 6, 10 кВ КРУН наружной установки	QS	0,01	3	0,2	3,5
Ячейка предохранителя 6, 10 кВ	FU	0,05	2,5	0,2	3
Линейный разъединитель 6, 10 кВ	QS	0,08	4,5	-	-
Шины ОРУ 35, 110 кВ на 1 присоединение	Ш	0,001	5	0,15	6
Шины РУ 6, 10 кВ на 1 присоединение	Ш	0,001	4	0,16	5
Сборка НН-0,4 кВ ТП	С 0,4	0,007	4	0,2	5

Коэффициент готовности – вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.

Из определения следует, что коэффициент готовности характеризует готовность объекта к применению по назначению только в отношении его работоспособности. Это означает вероятность застать объект в работоспособном состоянии в произвольный период времени, причем этот момент не может быть выбран в тех интервалах, где применение объекта исключено, например, при проведении плановых регламентных работ.

Наиболее часто применяется стационарное значение коэффициента готовности, которое определяется по формуле:

. (2.36)

Из этой формулы видно, что коэффициент готовности характеризует два различных свойства объекта – безотказность и ремонтопригодность. Коэффициент готовности является безразмерной величиной, значение которой лежит в пределах 0 < K_г < 1.

Для случайных величин Т₀ и Т_в с экспоненциальными законами распределений коэффициент готовности определяется через интенсивности отказов и восстановлений

. (2.36,а)

или для системы, состоящей из i элементов

. (2.36,б)

Оценку коэффициента готовности можно найти по результатам испытаний на надежность и восстановление одного элемента

, (2.36,в)

где N – число отказов и восстановлений одного и того же элемента; τ_j, τ_в – длительности работы и восстановления элемента; j – номер отказа.

Оценку можно определить и по результатам испытания на надежность большого числаN одинаковых восстанавливаемых элементов

, (2.36,г)

где N(t₀) – число исправных элементов в произвольный достаточно «удаленный» (от начала эксперимента) момент времени t₀, когда можно считать потоки отказов и восстановлений стационарными.

Коэффициент оперативной готовности – вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет безотказно работать в течение заданного интервала времени.

Как следует из определения, коэффициент оперативной готовности характеризует надежность объектов, необходимость применения которых возникает в произвольный момент времени, после которого требуется определенная безотказная работа. До этого момента такие объекты могут находиться как в режиме дежурства (при полных или облегченных нагрузках, но без выполнения заданных рабочих функций), так и в режиме применения – для выполнения заданных рабочих функций (задач, работ и т.д.). В обоих режимах возможно возникновение отказов и восстановление работоспособности объекта.

Коэффициент оперативной готовности определяют по формуле:

K_ог= K_г Р(t_п), (2.37,а)

где Р(t_п) – вероятность безотказной работы в интервале времени (t_з, t_п) при условии, что в момент времени поступления заявки на применение t_з объект находился в работоспособном состоянии; t_п – время работы объекта в режиме применения.

Для экспоненциального закона распределения и простейшего потока восстановления с интенсивностью μ коэффициент оперативной готовности можно определить по выражению

(2.37,б)

Коэффициент оперативной готовности почти всегда меньше K_г и равен ему только при t = 0.

Для определения величины K_ог используется статистическая оценка

, (2.37,в)

где N(τ) – число элементов, исправных в момент времени t и безотказно проработавших в течение времени τ.

Коэффициент оперативной готовности позволяет количественно оценить надежность объекта в аварийных условиях, т.е. до окончания выполнения какой-то эпизодической функции.

Коэффициент простоя – вероятность того, что система будет неисправной при длительной эксплуатации

.

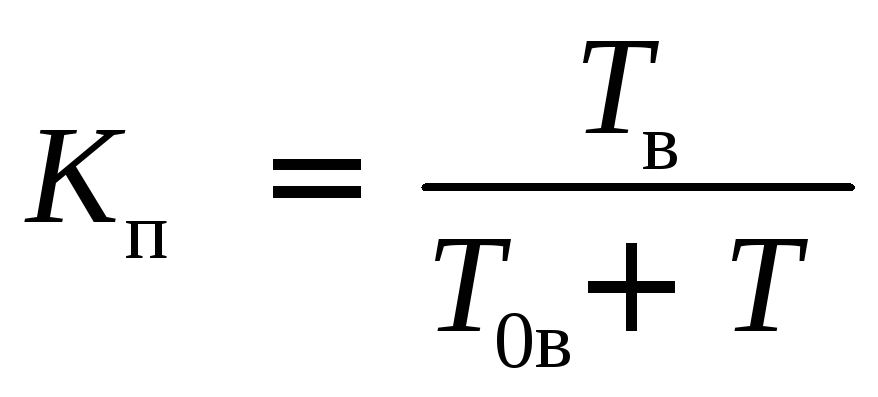Очевидно, что всегда имеет место равенство

K_г+ K_п= 1.

Относительный коэффициент простоя K_по – отношение коэффициента простоя к коэффициенту готовности

K_по =K_п / K_г = T_в / T₀.

Коэффициент технического использования K_ти учитывает дополнительные преднамеренные отключения элемента, необходимые для проведения планово-предупредительных ремонтов:

,

где Т_об – среднее время обслуживания, т.е. среднее время нахождения элемента в отключенном состоянии для производства планово-предупредительных ремонтов (профилактики).

Пример 2.10. Определить коэффициенты готовности, простоя и коэффициент технического использования для трансформатора с высшим напряжением 35, 110 кВ.

Решение. Из табл. 2.4 берем исходные показатели надежности λ = 0,03 год^–1, Т_В = 30 ч, Т_об = 11 ч., тогда

Т₀ = 1/ λ = 1/0,03 = 33,3 года.

; K_п = 1 – 0,999897 = 0,000103;