§3,5. Определение функции Грина в плоских областях.

Пусть на плоскости Оху поставлена смешанная краевая задача:

σ- плоская область и ее граница С=𝜕σ; х, у =const ≥ 0.

Формула решения этой задачи известна:

где – дифференциал дуги,– элемент площади.

-условие разрешимости задачи Неймана.

Для определения функции Грина поставим задaчу:

где и- функции Дирака.

Здесь функция описывает действие источника из точкии равнапри; «маленькая» функцияне имеет особенностей внутри площадкии описывает влияние зарядов, наведенных на граничном контуреC.

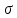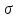На самом деле площадка является только сечением некоторой плоскостью длинного цилиндра с направляющим контуром С ; плоскость ортогональна к образующим цилиндра. Точечные заряды внутри областиявляются точками пересечения с областьюзаряженных прямых, параллельных образующим на поверхности цилиндра. Заданные функции распределения линейных зарядовF() –внутри областииf()-на граничном контуре С рассчитываются на единицу длины заряженной линии. Если длина отрезка заданного цилиндра гораздо больше всех остальных его геометрических размеров, то такой цилиндр можно считать бесконечно длинным.

В цилиндрической системе координат уравнение для функции Грина приможно записать в виде:

Решение этого уравнения Бесселя, описывающую действия источников, можно записать в виде

где - функция Ханкеля нулевого порядка и родаі=1 или 2. Если зависимость от времени принять , получим С=0 – нет приходящих волн и выбрать – для упрощения последующих расчетов (это возможно при решении однородного уравнения), то получим частное решениеи функция Грина будет

Функции Ханкеля нулевого порядка n=0 первого и второго рода ( i=1 или 2) при большом значении аргумента имеют асимптоту,а при малом значениибудет(здесь–постоянная Эйлера - Маскерони). Если зависимость от времени выбрать в виде, то везде получится- функция Ханкеля второго рода.

При ӕ=0 для уравнения Лапласа и Пуассона получим простое решениеили при С=1 и С=0.

При решении задачи Неймана в неограниченных областях по условию задачи требуется выполнение , значит постоянная.

§3,6. Решение плоской задачи Дирихле для уравнения Лапласа методом конформных отображений

Постановка краевой плоской задачи Дирихле для функции , где

Здесь - точка источникаиM(z)- точка измерения

Введем функцию аналитическую в областиD, где - функция искомая и- гармонически сопряженная к; обе эти функции неизвестны. Здесь обязательнов областиD.

Запишем интеграл Коши для искомой аналитической функции Ф(ζ) из области D.

где

Подберем функцию (здесьζ- переменная и z- параметр) удовлетворяющую следующим условиям:

1. - аналитическая пои непрерывная по

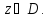
2. –конформно отображает односвязную область D в плоскости на кругтак, чтобы точкаz стала центром этого круга и выполнялось условие

3. при - отображение конформно всюду в областиD.

Разложим функциюв ряд Тейлоравида

здесь и

Рассмотрим логарифмическую производную

Так как имеет припростой нуль, тоимеет там простой полюс и функция- тейлоровская часть ряда.