
- •§3,1. Постановка и основные типы задач
- •§3,2. Решение краевых задач для уравнения Гельмгольца с использованием функции Грина (источника)
- •§3,3. Вывод общих формул для решения второй и третьей краевых задач.
- •§3,4. Определение функции Грина первой краевой задачи Дирихле для уравнения Гельмгольца.
- •§3,5. Определение функции Грина в плоских областях.
- •§3,6. Решение плоской задачи Дирихле для уравнения Лапласа методом конформных отображений
Часть третья
Решение стационарных задач математической физики методом функции Грина (источника)
§3,1. Постановка и основные типы задач
В предыдущих разделах решения задач находились в виде бесконечных рядов, что не всегда удобно при их использовании. Однако, в некоторых случаях (особенно при решении уравнений эллиптического типа для стационарных задач) решение можно получить в конечной замкнутой форме, использовав соответствующую разрешающую формулу. Нужно только суметь отдельно определить функцию Грина (источника) задачи в замкнутой форме (в виде единой формулы, а не в виде ряда). Это часто удается сделать, используя известный метод электростатического изображения заряда в граничной поверхности (метод В. Томсона-Кельвина).
Поставим
задачу для уравнения эллиптического
типа внутри пространственной области
V,
ограниченной замкнутой поверхностью
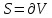 .
.

Здесь
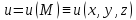 –
искомая функция;
–
искомая функция; –
точка измерения и
–
точка измерения и
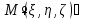
 ∪
∪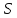 –точка
источника;
–точка
источника;
 – оператор Лапласа в трехмерной системе
координатOxyz.
– оператор Лапласа в трехмерной системе
координатOxyz.
Коэффициенты
 =
0 или 1 – постоянные;
=
0 или 1 – постоянные;
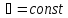 ≥0
– волновое число; при
≥0
– волновое число; при
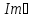 ≠0
в системе имеются потери. При ᴂ=0 получаем
уравнение Пуассона, а при ᴂ=
≠0
в системе имеются потери. При ᴂ=0 получаем
уравнение Пуассона, а при ᴂ=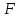 =0
– уравнение Лапласа. При
=0
– уравнение Лапласа. При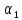 =0
и
=0
и =1
получаем граничное условие первого
рода
=1
получаем граничное условие первого
рода =
=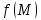 (условие Дирихле), а при
(условие Дирихле), а при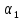 =1
и
=1
и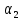 =0
– условие второго рода
=0
– условие второго рода =
=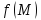 (условие Неймана); здесь
(условие Неймана); здесь – внешняя нормаль к граничной поверхности
– внешняя нормаль к граничной поверхности
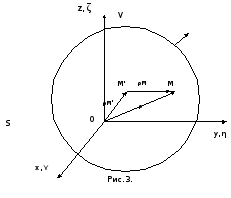 .
.
Введем
также радиус-векторы точек
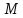 и
и
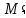 ,
обозначим
,
обозначим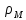 =
=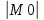 ,
, =
=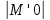 и
и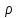 =
=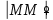 ˃
0.
˃
0.
Рассматриваемые задачи называются по названию граничного условия, затем указывается для какого уравнения.
Для всех трех вариантов, поставленных выше краевых задач, можно доказать существование и единственность функции Грина; вид этой функции зависит только от формы граничных условий.
§3,2. Решение краевых задач для уравнения Гельмгольца с использованием функции Грина (источника)
Из формулы Гаусса-Остроградского:
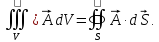
легко
получить формулу Грина. Пусть вектор
 где
где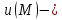 искомая функция и
искомая функция и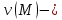 некоторая вспомогательная функция. Так
как вектор
некоторая вспомогательная функция. Так
как вектор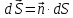 (
(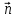 – орт нормали к поверхности
– орт нормали к поверхности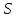 ),
то проекция
),
то проекция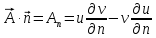 (здесь
(здесь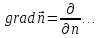 -
производная по направлению нормали).
Дивергенцию вектора
-
производная по направлению нормали).
Дивергенцию вектора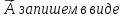

Если
ввести новый оператор
 ,
то получим
,
то получим
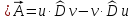 и запишем формулу ( не функцию!) Грина
и запишем формулу ( не функцию!) Грина

Если
область
 неограниченна, то при
неограниченна, то при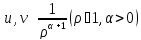 несобственные интегралы сходятся.
несобственные интегралы сходятся.
В
частном случае
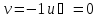 формула Грина принимает вид
формула Грина принимает вид
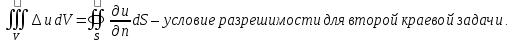
Все приведенные формулы можно использовать и для решения плоских или одномерных задач.
Поставим первую краевую задачу Дирихле для уравнения Гельмгольца вида
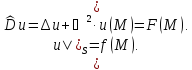
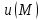 –искомая
функция.
–искомая
функция.

Для
решения задачи используем аналогичную
модельную краевую задачу для вспомогательных
функций
 =
=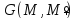 – функции Грина
– функции Грина – точка измерения, параметры интегрирования;
– точка измерения, параметры интегрирования;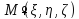 – точки источников, переменные
интегрирования), для которой
– точки источников, переменные
интегрирования), для которой
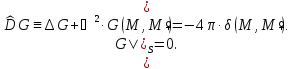
Здесь
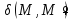 - дельта-функция Дирака, равная
- дельта-функция Дирака, равная
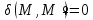 при
при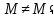 и
и при
при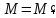 .
Интеграл от произведения сходящийся и
равен
.
Интеграл от произведения сходящийся и
равен

Подставим
уравнения для функции
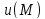 и
и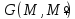 в формулу Грина и получим
в формулу Грина и получим
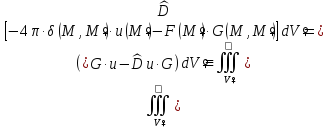
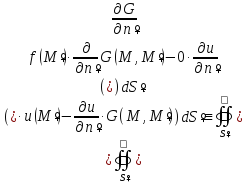
Теперь формула для решения первой краевой задачи Дирихле примет окончательный вид
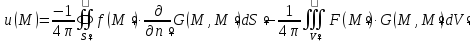
Если
функция Грина
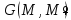 известна, то решение краевой задачи
Дирихле сводится просто к квадратурам.
известна, то решение краевой задачи
Дирихле сводится просто к квадратурам.
Функция,
удовлетворяющая уравнению Лапласа
 ,
называется гармонической, из свойств
этих функций следует, что функция Грина
,
называется гармонической, из свойств
этих функций следует, что функция Грина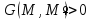 положительна в области гармоничностиV;
она
положительна в области гармоничностиV;
она
 в особых точках (точках зарядов) и
в особых точках (точках зарядов) и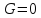 (достигаетmin)
только на границе S
области V.Решение
краевой задачи Дирихле
(достигаетmin)
только на границе S
области V.Решение
краевой задачи Дирихле
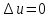 и
и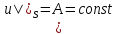 можно записать
можно записать

откуда
получим
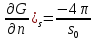 ,
где
,
где – площадь поверхностиS.
– площадь поверхностиS.
