
МАТЕМАТИКА 1 СЕМЕСТР АНАЛИЗ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
.pdf
f a и f b разных знаков, то существует на интервале a, b точка x3 такая, что
f x3 0 .
Замечание. Теорема перестает быть верной для функции, непрерывной на интервале, или функции, имеющей разрыв на отрезке. Например, функция
f (x) |
1 |
непрерывна на интервале (0,1), но является на |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
x |
|
|
1 |
|
y |
|
|
|
|
|
нем неограниченной, так как |
|
|
. Кроме |
|
|
|
|
|||||
lim f (x) lim |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
x 0 |
x 0 |
x |
|
|
y f x |
|
||
того, эта функция не достигает на интервале (0,1) наи- |
|
|
|
|
|
|||||||
большего значения. |
f x |
|
|
|
|
a |
x0 |
b |
x |
|||
|
Другой пример: функция |
имеет разрыв в точ- |
o |
|||||||||
|
|
|
|
|||||||||
ке x0 |
(ее график изображен на рис. 14) и, хотя значения |
|
|
|
|
|
||||||
f a |
и f b разных знаков, но ни в какой точке функция |
|
|
Рис.14 |
|
|
||||||
f x не принимает нулевые значения.
Глава 2. Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной изучает одно из основных математических понятий понятие производной и дифференциала и их применение, в частности для исследования функций.
6. Производная и дифференциал функции
Понятие производной широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости протекания различных процессов.
6.1. Определение производной
Рассмотрим функцию |
|
y f x . Придадим аргументу x приращение |
x . |
||||||||||||||||
Тогда функция y f x получит приращение |
f x f x x f x , которое |
||||||||||||||||||
характеризует изменение функции |
f x |
на отрезке x, x x . Средняя скорость |
|||||||||||||||||
изменения функции на этом отрезке равна |
|
f x |
, а скорость изменения функ- |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
f x |
|
|
|
|
|
|
|
x |
|
|||||
ции f x в точке x есть lim |
|
. |
Этот предел, если он существует, называет- |
||||||||||||||||
|
|
|
|||||||||||||||||
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ся производной f x |
функции |
f x |
в точке x . Итак, по определению |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f x lim |
f x |
lim |
f x x f x |
|
. |
|
|
||||||||||
|
|
x |
|
|
|
|
|||||||||||||
|
|
|
x 0 |
|
x 0 |
|
|
x |
|
|
|
||||||||
Для функции y f x |
приняты и другие обозначения производной: y x , |
yx . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 6.1. Доказать, что |
|
sin x cos x |
|
, |
|
cos x sin x |
. |
|
|||||||||||
Решение. Воспользуемся определением производной и первым замечательным пределом:
21
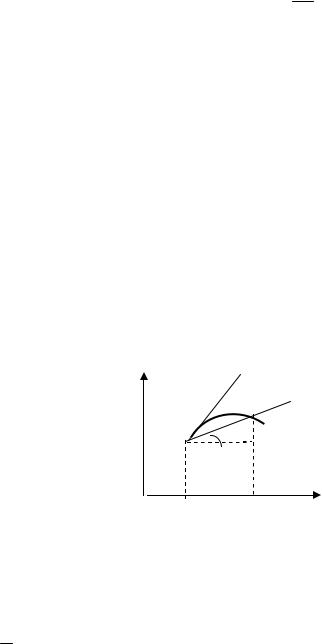
sin x lim |
sin x x sin x |
|
0 |
|
lim |
||
|
|
|
|
||||
x |
0 |
||||||
x 0 |
|
|
|
x 0 |
|||
Итак, sin x cos x. Аналогично доказывается,
|
x |
|
|
x |
||||
2 sin |
|
|
cos x |
|
|
|||
2 |
2 |
|||||||
|
|
|
|
1 cos x. |
||||
2 |
x |
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
|||||
|
2 |
|
|
|
|
|||
что cos x sin x.
Пример 6.2. Доказать, что |
ln x |
1 |
|
, |
loga x |
1 |
|
. |
|
x |
x ln a |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Решение. Воспользуемся определением производной:
|
|
|
|
|
|
|
|
|
|
x x |
|
|
x |
|||||||
|
ln x x |
ln x |
0 |
|
|
ln |
|
|
|
|
|
|
ln 1 |
|
|
|||||
|
|
|
x |
|
|
|
||||||||||||||
ln x lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
lim |
|
x |
. |
||||
x |
|
|
|
|
|
x |
|
|
|
|
||||||||||
x 0 |
|
|
0 |
|
|
x 0 |
|
|
|
|
x 0 |
x |
||||||||
При x 0 и фиксированном |
x функция |
|
|
x |
эквивалентна функции |
|||||||||||||||
ln 1 |
|
|
|
|
||||||||||||||||
|
|
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x
x
(см. пример 4.9), поэтому
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
ln 1 |
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||
|
|
|
ln x lim |
|
|
|
|
lim |
|
. |
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
|
|
x 0 |
|
|
|
x 0 x |
|
x |
|
|
|||||||||
|
|
ln x |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
||
Так как |
log a x |
, то log a x |
|
ln x |
|
ln x |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ln a |
|
|
ln a |
|
|
|
|
|||||||||||||
|
|
|
|
|
ln a |
|
|
|
|
ln a x |
|
|||||||||
|
6.2. Геометрический и физический смысл производной |
|
|
|
||||||||||||
|
Рассмотрим на кривой |
y f x |
точки M 0 , |
M и секущую M 0 M (рис.15). |
|
|
||||||||||
|
При движении точки M по этой кривой к точке |
M0 секущая |
M 0 M займет свое |
|
|
|||||||||||
|
предельное положение M 0T . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||||
|
Предельное положение M 0T секущей M 0 M при стремлении точки M по кривой |
|
|
|||||||||||||
|
к точке M0 , называется касательной к данной кривой в точке |
M0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Найдем угловой коэффициент kсек невертикальной |
y |
|
T |
|
|
||||||||||
|
секущей и угловой коэффициент kкас |
невертикальной |
|
|
M |
|
|
|||||||||
|
касательной: |
kсек tg |
f x0 |
|
, |
|
|
|
|
M0 |
|
f x0 |
|
|
||
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
kкас |
lim kсек lim |
f x0 |
|
|
f |
x0 . |
|
|
x |
|
x |
||||
|
x |
|
|
|
x |
|||||||||||
|
|
M M0 |
x 0 |
|
|
|
|
|
|
x 0 |
||||||
|
Из этого равенства вытекает геометрический смысл |
|
Рис. 15 |
|
|
|||||||||||
|
производной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Значение производной |
f x0 равно угловому коэффициенту касательной, про- |
|
|
||||||||||||
|
веденной к кривой y f |
x |
в точке M0 |
с абсциссой x0 : |
f x0 kкас |
|
|
|
||||||||
Если угол наклона секущей стремится к 2 (рис.16), то касательная – вертикальна.
22
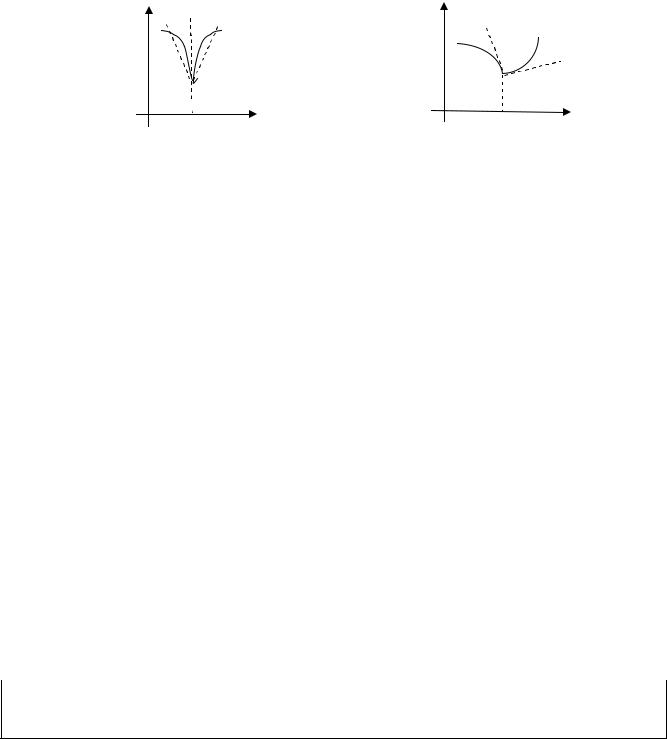
При этом kсек при M M 0 , kкас lim kсек . Следовательно, f x0 .
M M0
Кривая y f x может не иметь касательную ( рис.17) в смысле приведенного выше определения, но имеет правостороннюю касательную l1 с угловым
коэффициентом k1 f x0 0 |
и левостороннюю касательную l 2 с угловым ко- |
||||||||||||||
эффициентом k2 f x0 0 , при этом k1 k 2 . Тогда |
f x0 не существует. |
||||||||||||||
|
|
|
y |
T |
M |
|
|
|
|
y |
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
M0 |
|
|
|
|
|
|
M0 |
l1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
o |
x0 |
|
x |
|
|
o |
|
x |
x |
|||
|
|
|
|
Рис.16 |
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис.17 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Прямая, проходящая через точку касания перпендикулярно касательной к |
|
||||||||||||
|
|
кривой, |
называется нормалью к этой кривой. |
1 |
|
|
|
|
|||||||
|
|
Угловой коэффициент нормали |
kнорм. |
|
. |
|
|
|
|||||||
|
|
k кас. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение прямой, если известен ее угловой коэффициент и точка |
M 0 x0 , y0 , |
||||||||||||||
имеет вид: |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
|
|
|
y y0 |
k x x0 |
|
|
|
|
|
|
|
||||
Для записи уравнения |
|
нормали к кривой |
y f x |
следует по- |
|||||||||||
касательной или |
|||||||||||||||
ложить y0 f x0 и |
k k кас |
или k k норм |
соответственно. |
|
|
||||||||||
|
Физический смысл |
производной заключается в том, что значение производ- |
|||||||||||||
ной f x есть скорость изменения функции f x |
в точке |
x . Поэтому |
|||||||||||||
1) если задан закон движения материальной точки по прямой |
S S t , то |
||||||||||||||
скорость движения |
v S t , а ускорение a есть «скорость изменения скорости», |
||||||||||||||
то есть a v t ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
если |
Q Q t |
есть количество электричества, проходящего через попе- |
||||||||||||
речное сечение проводника за время t , то Q t I есть сила тока ; |
|
|
|||||||||||||
3) |
если |
N N t |
есть количество вещества, вступающего в химическую ре- |
||||||||||||
акцию за время t , то N t есть скорость химической реакции. |
|
|
|||||||||||||
|
|
|
6.3. Дифференцируемые функции. Дифференциал |
|
|
||||||||||
|
|
|
|||||||||||||
Определение. Функция |
f x |
называется дифференцируемой в точке x , если |
|||||||||||||
она имеет производную в этой точке.
Операция отыскания производной называется дифференцированием функции.
Пусть функция дифференцируема, то есть имеет производную
23

|
|
|
f x |
|
lim |
f x |
. |
|
|
||
|
|
|
|
||||||||
|
|
|
|
|
x 0 |
x |
|
||||
Тогда согласно теореме 3.1 о связи функции с ее пределом: |
|||||||||||
|
|
|
f x |
|
f |
|
x x , |
|
|||
|
|
|
x |
|
|||||||
где x |
есть функция бесконечно малая при x 0 . |
Поэтому приращение |
|||||||||
дифференцируемой функции представимо в виде |
|
||||||||||
|
|
|
|
(6.1) |
|||||||
|
|
f x f x x x x . |
|||||||||
Выражение f x x называют дифференциалом функции и обозначают d f x :
|
|
d f x f x x . |
|
|
|
Отметим следующие моменты. |
|
|
|||
1). Дифференциал функции линеен относительно x |
и имеет при x 0 тот же |
||||
порядок малости, что и x . |
|
|
|||
2). Второе слагаемое в равенстве (6.1) является при |
x 0 бесконечно малой |
||||
o x более высокого порядка, чем x . |
|
|
|||
3). Приращение дифференцируемой функции f x представимо в виде |
|||||
|
|
|
|||
|
f x f x x o x d f x o x . |
||||
4). Так как df x f x x , то для функции, равной x , имеем d x x x x , то есть x d x . Поэтому
|
|
|
|
|
|
|
|
|
d f x |
|
|
|
|
|
df x f |
|
x d x |
|
|
|
|
||||
|
|
, |
f |
x d x |
. |
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
6.4. Связь между непрерывностью и дифференцируемостью |
||||||||||||
|
|
|
||||||||||
|
Если функция дифференцируема , то она непрерывна. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, для дифференцируемой функции f x f x x o x . Отсюда следует, что бесконечно малому приращениюаргумента x соответствует бесконечно малое приращение функции f x и, значит, функция f x непрерывна в точке x .
Непрерывная функция может не быть дифференцируемой.
Примером такой функции является функция f x x . Эта функция непрерыв-
на при x 0 , так как lim |
f x lim |
|
x |
|
0 f 0 . Но функция не |
y |
|
|
|||||
x 0 |
x 0 |
|
|
|
|
|
|
|
|
дифференцируема при x 0 , так как |
|
|
|
|
|
|
|||||||||
|
f 0 |
|
f 0 x |
f 0 |
|
|
x |
|
|
1, |
x 0, |
|
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0, |
о |
|
|
x |
|
x |
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
1, |
|
||||||
и, значит, f 0 lim |
f 0 |
|
не существует; функция f x не |
Рис.18 |
|||||||||||
x |
|||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
||||
y x
x
24
дифференцируема при x 0 . Отметим, что существуют односторонние пределы f 0 1, f 0 1. С геометрической точки зрения это означает, что в точке
0, 0 существуют, но не совпадают правосторонняя касательная с угловым ко-
эффициентом k 1 и левосторонняя касательная с угловым коэффициентом k 1 (рис.18).
6.5. Производная суммы, произведения, частного
Отыскание производных непосредственно по определению неудобно и сложно. Для этого существуют ряд правил и формул.
Теорема 6.1. Пусть функции u u x , v v x − дифференцируемы. Тогда сумма, разность, произведение этих функций, а при v x 0 и частное дифференцируемы, причем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
||||
u v |
|
u |
|
|
, |
uv |
|
|
|
, |
|
u v u v |
|
|
. |
|||
|
|
|
|
|
|
|||||||||||||
|
|
v |
|
u v uv |
|
v 2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|||
Выведем одну из этих формул, например, вторую.
Так как u x u x x u x , то u x x u x u x .
Аналогично, v x x v x v x .
Найдем приращение функции f x u x v x :
f x f x x f x u x x v x x u x v x
u x u x |
v x v |
x u x v |
x u x v x v x u x u x v x . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
f x |
u x |
v x |
v x |
|
u x |
u x |
v x |
|
|
. |
|
(6.2) |
|||||||||||
|
|
|
|
|
x |
|
|
x |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||
Функция u x |
дифференцируема и, следовательно, непрерывна. Поэтому |
|
|
|||||||||||||||||||||||||
u x 0 при x 0 . Переходя в равенстве (6.2) |
к пределу при x 0 , полу- |
|||||||||||||||||||||||||||
чим: u x v x |
|
f |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
x или uv |
|
|
|
. |
||||||||
|
|
x u x v |
x v x u |
v |
|
u v uv |
||||||||||||||||||||||
Остальные формулы выводятся аналогично. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следствие 1. |
|
tg x |
|
1 |
|
|
, |
|
ctg x |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
||||||
|
cos2 |
x |
|
sin2 x |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Действительно, по формуле для производной частного имеем:
|
|
|
|
sin x |
|
cos x sin x cos x |
|
|
cos |
2 |
x sin |
2 |
x |
|
1 |
|
|
sin x |
|
|
|
|
|
|
|
|
|
||||||||
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
cos2 x |
|
|
cos2 x |
|
|
cos2 |
|
|||||||
cos x |
|
|
|
|
|
|
|
|
|
x |
|||||||
Аналогично выводится формула для производной ctg x .
Следствие 2. Дифференциалы суммы, произведения, частного дифференцируемых функций u u x , v v x вычисляются по формулам:
d u v du dv , |
d u v v du u dv , |
u |
|
v du u dv |
v 0 |
|
. |
||
d |
|
|
|
|
|||||
|
v2 |
||||||||
|
|
v |
|
|
|
|
|||
25

Докажем, например, вторую формулу. Воспользуемся определением дифференциала и производной произведения:
d uv uv dx u v uv dx v u dx u v dx v du u dv .
Примеры для самостоятельного решения
Найти производные следующих функций:
|
а) f (x) |
3 |
|
|
5 ; |
б) |
f (x) x tg x ; |
в) |
f (x) 5 |
x |
. |
|
|||||
|
cos x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|||||
Ответы: |
|
sin x |
; |
б) |
|
|
|
x |
; в) |
|
ln x 1 |
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
а) f (x) 3 |
cos2 x |
f (x) tg x |
|
f (x) |
ln2 x |
||||||||||||
|
|
|
|
|
|
|
cos2 x |
|
|
|
|||||||
|
|
6.6. Производная сложной функции |
|
||||||||||||||
Пусть |
y f u , |
u x . Тогда |
y f x сложная функция с промежу- |
||||||||||||||
точным аргументом u , независимым аргументом x . |
|
|
|
|
|
|
|||||||||||
|
|
|
|||||||||||||||
Теорема 6.2. Пусть функции y f u , |
u x |
дифференцируемы. Тогда |
|||||||||||||||
сложная функция |
y f |
x дифференцируема и для ее производной справед- |
||||||||||||||||
лива формула: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
yu ux . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство. Для дифференцируемой функции |
y f u |
имеем: |
||||||||||||||||
|
|
|
|
|
y yu u u u , |
|
|
|
(6.3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где u бесконечно малая функция при u 0 . |
|
|
|
|
|
|||||||||||||
Разделив равенство (6.3) на |
x , получим: |
|
y |
yu |
u |
|
u |
|
||||||||||
|
x |
x |
x u . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдем в этом равенстве к пределу при |
x 0 : |
|
|
|
|
|
||||||||||||
|
|
lim |
y |
y |
lim |
u |
|
lim |
u |
lim u . |
(6.4) |
|||||||
|
|
|
|
x |
||||||||||||||
|
|
x 0 x |
u |
x 0 x |
x 0 |
x 0 |
|
|
|
|
||||||||
Функция u x |
дифференцируема, а значит, и непрерывна. Поэтому ее при- |
|||||||||||||||||
ращение u 0 при |
x 0 . Тогда u 0 при |
x 0 |
и равенство (6.4) |
|||||||||||||||
примет вид: yx yu ux ux |
0 yu ux . |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, для нахождения производной сложной функции надо производную функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько.
Пример 6.3. Найти производную функции |
y ln3 sin x . |
|
|
|||||||||||
Решение. Данную сложную функцию можно представить в виде |
|
y u3 , где |
||||||||||||
u ln v , v sin x . |
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
1 |
cos x 3ln |
2 |
sin x |
1 |
cos x 3ctg x ln |
2 |
sin x. |
|
|
|
|||||||||||||
yx |
yu uv vx 3 u |
|
v |
|
sin x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
26

В дальнейшем, при приобретении навыка, промежуточные аргументы u, v,... можно вводить «мысленно» и не писать их. Например,
|
|
tg2 x3 |
|
2 tg x3 |
1 |
|
|
3 x2 . |
|
|
|
|
|
cos |
2 |
x |
3 |
|
|||
|
|
|
|
|
|
|
|
|
||
|
Примеры для самостоятельного решения |
|||||||||
Найти производные следующих функций: |
а) |
y ln tg x2 ; б) |
y sin3 x5 ; |
|||||||
Ответы: а) y |
4 x |
; б) y 15 x4 sin2 x5 |
cos x5 . |
|
||||||
2 |
|
|||||||||
|
sin 2x |
|
|
|
|
|
|
|
|
|
|
6.7. Логарифмическое дифференцирование |
|||||||||
В ряде случаев для нахождения производной функции |
y f x удобно ра- |
|||||||||
венство y f x |
сначала прологарифмировать, а затем продифференцировать. |
|||||||||
Такой прием называют логарифмическим дифференцированием. Его полезно применять для дифференцирования произведения многих сомножителей, или для дифференцирования частного, числитель и знаменатель которого содержит несколько множителей, или для дифференцирования степенно-показательных
функций |
u x v x . При этом следует учесть, |
что функция |
|
ln y сложная, так как |
|||||||||||||||||||||||||||||||||||
y y x |
и поэтому |
ln y |
ln y |
yx |
1 |
yx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6.4. Доказать, что |
|
|
|
ax a x lna |
|
, |
|
|
|
|
|
|
|
e x e x |
. |
|
|
||||||||||||||||||||||
Решение. Прологарифмируем равенство y ax : |
ln y xln a ; |
затем продиффе- |
|||||||||||||||||||||||||||||||||||||
ренцируем равенство по x : |
1 |
yx lna и выразим |
|
|
|
yx : |
|
|
yx |
y lna a x lna . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При a e получим: ex ex . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 6.5. Доказать, что |
|
|
xa a xa 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Прологарифмируем равенство |
y x a : |
ln y a ln x ; |
затем продиффе- |
||||||||||||||||||||||||||||||||||||
ренцируем по x : |
1 |
yx a |
1 |
|
и выразим |
yx : |
yx |
|
|
a |
y |
|
a |
|
xa |
a xa 1 . |
|||||||||||||||||||||||
y |
x |
|
x |
|
x |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x 5 2 esin x |
|
|
|
|
|
|||||||||||||||||
Пример 6.6. Найти производную функции y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
(x 1)4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Найти y |
как производную частного слишком громоздко. Удобнее |
||||||||||||||||||||||||||||||||||||||
применить логарифмическое дифференцирование: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ln y ln |
x 5 2 / 3 esin x |
ln x 5 |
2 / 3 |
ln esin x ln x 1 |
4 |
, |
|
|
|
|
ln y |
2 |
|
ln x 5 sin x 4 ln x 1 . |
|||||||||||||||||||||||||
|
(x 1)4 |
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
1 |
|
|
1 |
|
|||||
Продифференцируем последнее равенство по x : |
|
y |
y |
|
|
3 x 5 cos x 4 x 1 . |
|||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
27

Выразим y : |
|
2 |
|
4 |
|
|
|
|
y y |
|
cos x |
|
|
|
|
||
3 x 5 |
x 1 |
|||||||
|
|
|
|
|
||||
3 x 5 2 esin x |
|
2 |
|
4 |
|
|
|
|
|
|
|
cos x |
|
|
. |
|
4 |
|
|
|
|||
(x 1) |
|
3 x 5 |
|
x 1 |
|
||
|
|
|
|
||||
Пример 6.7. Найти производную функции y x tg x .
Решение. Так как основание и показатель степени переменны, то следует применить логарифмическое дифференцирование. Прологарифмируем исходное ра-
венство: ln y ln xtg x |
или ln y tg x ln x . Теперь продифференцируем по x , ис- |
пользуя формулу для производной сложной функции (в левой части) и формулу для производной произведения ( в правой части):
1y y tg x ln x
Тогда |
|
1 |
|
1 |
|
|
y y |
|
ln x tg x |
|
|
x |
|
|
x |
|||||
|
cos2 x |
|
|
|
||
tg x
tg x
ln x
ln x
cos2 x
1 |
ln x tg x |
1 |
. |
cos2 x |
|
||
|
x |
||
tg x .
|
|
|
|
Примеры для самостоятельного решения |
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 |
|
x 2 2 |
|
y xx2 1 . |
|||||||||||||||
Найти производные следующих функций: а) |
|
y |
x 1 |
; б) |
||||||||||||||||||||
|
|
x 5 3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
x 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
x2 1 |
|
|
x2 1 |
|
|
||||
Ответы: а) |
|
|
|
|
|
|
|
|
|
|
|
; |
б) |
x |
2x ln x |
|
. |
|||||||
y |
x 5 3 |
3(x 1) |
x 2 |
x 5 |
y |
|
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6.8. Производная обратной функции
Теорема 6.3. Пусть функция y f x монотонна и дифференцируема на интервале a,b , причем y x 0 . Тогда обратная функция x f 1 y дифференцируе-
ма и ее производная вычисляется по формуле |
xy |
1 |
. |
|
|||
|
|
yx |
|
Доказательство теоремы рассматривать не будем.
Следствие. Производные обратных тригонометрических функций вычисляются по формулам:
arcsin x |
|
1 |
, arccos x |
|
|
1 |
|
, |
arctg x |
|
1 |
|
|
|
, |
arcctg x |
|
|
1 |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 x2 |
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
1 x2 |
|
|
|
|
1 x2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выведем первую из этих формул. Рассмотрим функцию x sin y, |
y |
|
|
, |
|
|
. |
|
|||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
Эта функция монотонна, дифференцируема и xy cos y 0 |
|
|
на рассматриваемом |
||||||||||||||||||||||||||||||||
интервале. Поэтому обратная функция |
y arcsin x дифференцируема, причем |
||||||||||||||||||||||||||||||||||
|
|
|
yx |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
xy |
cos y |
|
1 sin2 y |
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Перед корнем взят знак плюс, так как cos y 0 при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y |
|
|
|
|
, |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично выводится формула для производной arctg x . Кроме того,
28

arcsin x arccos x |
|
, |
|
arctg x arcctg x |
|
|
. |
|
|
|
||||||||||||
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поэтому arccos x arcsin x , |
arcctg x arctg x . |
|
|
|
|
|
|
|
|
|||||||||||||
Примеры для самостоятельного решения |
||||||||||||||||||||||
Найти производные следующих функций: |
|
в) ln x |
|
|
|
|
|
. |
||||||||||||||
а) y arctg e 2x , б) |
|
|
|
|
, |
|
|
|
||||||||||||||
y arccos |
|
|
1 x2 |
|||||||||||||||||||
|
1 3x |
|||||||||||||||||||||
Ответы: а) yx |
2 e 2x |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
; |
б) |
y |
|
|
|
|
; в). y |
|
|
|
|
|
. |
||||||||
1 e 4x |
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
3x 9x2 |
|
|
1 x2 |
||||||||||||||||||
6.9. Таблица производных
Приведем сводку полученных нами правил и формул дифференцирования .
Правила дифференцирования
1. u v u v ,
2. |
uv |
|
|
|
|
|
|
, |
|||
|
u v uv |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
u |
|
|
|
|
|
|||||
3. |
|
|
u v uv |
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
v 2 |
|
|
|||||
4. |
v |
|
|
|
|
|
|
|
|||
yx |
yu ux , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
5. |
yx |
|
1 |
|
|
(xy |
|||||
xy |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
вчастности,
вчастности,
где y y u , u
0) .
c u c u , где с − число,
|
|
|
|
c v |
|
c |
|
, где с − число, |
|||
|
|
|
|
||
|
v 2 |
||||
v |
|
|
|||
u x ,
Формулы дифференцирования
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||
1. |
|
a x a 1 , |
|
|
|
в частности, |
|
|
|
|
x |
|
|
|
|
|
; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
2 |
|
x |
|||||||||
2. |
a x a x lna , |
|
|
|
|
|
в частности, |
|
e x e x ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
3. |
loga x |
|
|
1 |
|
|
, |
|
в частности, |
|
ln x |
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x lna |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
sin x cos x, |
|
|
|
cos x sin x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5. |
tg x |
1 |
|
|
, |
|
|
|
|
|
ctg x |
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
cos 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
6. |
arcsin x |
1 |
|
|
|
|
, |
arccos x |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7. |
arctg x |
|
1 |
|
|
|
, |
|
|
|
arcctg x |
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8. sh x ch x, |
|
|
|
ch x sh x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
9. |
th x |
1 |
|
, |
|
|
|
|
cth x |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ch2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
sh2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
29

|
|
|
|
|
|
6.10. Производные высших порядков |
|
|
|
||||||||||||
|
Пусть y f x − дифференцируемая функция. Производная y f x также |
||||||||||||||||||||
является функцией от x . Ее производная |
y x |
называется производной вто- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x , |
|
|
|
|
x , |
|
d 2 f |
|
||
рого |
порядка |
|
и |
обозначается |
y |
или |
f |
|
или |
d x2 . Аналогично |
|||||||||||
|
|
|
|
||||||||||||||||||
y x |
y x , |
y x y 4 x ,… |
Производной n −го порядка функции на- |
||||||||||||||||||
зывается производная от производной n 1 −го порядка: |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y n x y n 1 x |
|
|
|
|
|
|||||||||
Пример 6.8. Найти формулу для производной |
n −го порядка функции y a x . |
||||||||||||||||||||
Решение. |
y a x ln a, |
y a x ln a a x ln2 a, ..., y n a x lnn a . |
|
|
|
||||||||||||||||
|
6.11. Функции, заданные параметрически, и их производные |
||||||||||||||||||||
|
Пусть зависимостьмеждуаргументом x и функцией y задана при помощи уравнений: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x x t , |
y y t , |
|
|
(6.5) |
||||||||
где t вспомогательная переменная, |
называемая параметром. |
Будем предпола- |
|||||||||||||||||||
гать, |
что функция |
x x t имеет обратную функцию |
t t x . |
Тогда равенства |
|||||||||||||||||
(6.5) |
определяют сложную функцию |
y y t x , |
заданную параметрическими |
||||||||||||||||||
уравнениями (6.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||||||||||||
Теорема 6.4. |
Пусть функция |
|
y y x |
задана параметрическими уравнениями |
|||||||||||||||||
x x t , y y t , где x t , y t |
|
дифференцируемые функции, |
причем x t 0 и |
||||||||||||||||||
функция x t имеет обратную. |
Тогда функция |
|
y y x |
дифференцируема, а ее |
|||||||||||||||||
производная находится по формуле: yx yt .
xt
Если функции x t , y t дважды дифференцируемы, то существует производная
|
|
|
|
|
|
|
|
|
t |
|
|
второго порядка |
|
|
yx |
. |
|
|
|
||||
yxx , причем |
yxx |
xt |
|||
|
|
|
|
||
Доказательство. Как уже отмечалось, равенства (6.5) определяют сложную функцию y y t , где t t x . По правилу дифференцирования сложной функ-
ции и обратной функции
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
yt |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
yx yt |
tx yt |
|
xt |
|
xt |
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично |
|
|
|
|
. |
|
||||||||||
yxx yx |
x |
yx |
t |
tx |
yx |
t |
xt |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
30
