Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИКА 1 СЕМЕСТР АНАЛИЗ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

.pdf

Скачиваний:

Добавлен:

13.03.2016

Размер:

1.02 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет-УПИ»

Р.М. Минькова

Дифференциальное исчисление функции одной переменной

Учебно-методическое пособие

Научный редактор доц. В.Б. Грахов

Печатается по решению редакционно-издательского совета ГОУ ВПО УГТУ-УПИ

Екатеринбург

2006

УДК 517.5: 517.28 (075.8) ББК 22.161.я73 М 62

Рецензенты:

кафедра высшей математики Уральского государственного экономического университета (зав. кафедрой проф., канд. физ.-мат. наук Н.И. Чвялева);

проф., д-р физ.-мат. наук И. В. Мельникова (Уральский государственный университет им. А.М, Горького, кафедра математического анализа)

Автор Р.М. Минькова

М 62 Дифференциальное исчисление функции одной переменной: учебно-

методическое пособие по курсу «Высшая математика» / Р.М.Минькова. Екатеринбург: ГОУ ВПО УГТУ−УПИ, 2006. 56 с.

ISBN 5-321-00547-8

В пособии рассмотрены основные понятия математического анализа – понятие предела, понятия производной и дифференциала функций одной переменной, общие теоремы анализа, исследование функций и построение их графиков.

Приведено решение типовых задач. Предложены примеры для самостоятельного решения с ответами.

Пособие предназначено для студентов дистанционной и заочной форм обучения.

Библиогр.: 11 назв. Рис.32.

УДК 517.5: 517.28 (075.8) ББК 22.161.я73

Подготовлено кафедрой «Вычислительные

методы и уравнения математической физики»

и факультетом дистанционного образования

ISBN 5-321-00547-8

©ГОУ ВПО «Уральский государственный технический университет − УПИ», 2006

Оглавление

Глава 1. Предел и непрерывность функции одной переменной

1.Определение предела …………………..…………………....................…...…..………….4

1.1.Окрестности конечной точки и бесконечности…….…...............………...…...…4

1.2.Предел функции ………………………..…..………….............…..…...……..…....5

1.3.Предел последовательности………………....……..…...........……...….…….……6

1.4.Односторонние пределы функции………….….…..............………………….......7

2.Теоремы о функциях, имеющих конечный предел………...................….........…….…...7

3.Бесконечно малые функции……………………………….....................…….....…….…..9

3.1.Определение и основные свойства………..………...…………..…..............…....9

3.2.Отношение бесконечно малых. Неопределенность 0 / 0 ..………...........…….10

3.3.Первый замечательный предел………..…..……..…………...............................11

3.4.Сравнение бесконечно малых………….…..…..…………..…………...........….12

4.Бесконечно большие функции………………...................……....………........................14

4.1.Определение и основные свойства………...……..………............………....….14

4.2. Неопределенности / ,

0 ,

………………............…..……....….15

4.3.Второй замечательный предел. Неопределенность 1 …............…….…….16

5.Непрерывные функции…………………………….....…….................…………………18

5.1.Функции, непрерывные в точке……..………………...…............……….…….18

5.2.Точки разрыва функции и их классификация……...….….............……..…….18

5.3.Функции, непрерывные на отрезке...……..…………...….................................20

Глава 2. Дифференциальное исчисление функции одной переменной

6.Производная и дифференциал функции………………...….....................….....……….21

6.1.Определение производной…………………………….….…..........….……......21

6.2.Геометрический и физический смысл производной……..............….…..…....22

6.3.Дифференцируемые функции. Дифференциал…………..…........…..….….....23

6.4.Связь между непрерывностью и дифференцируемостью.........……...……...24

6.5.Производная суммы, произведения, частного……………..............….…..…..25

6.6.Производная сложной функции……………………………..............….…..….26

6.7.Логарифмическое дифференцирование………………….….........……...……27

6.8.Производная обратной функции……………………………..........……....…...28

6.9.Таблица производных………………………………………..........…....………29

6.10.Производные высших порядков………………………….........…….....…….30

6.11.Функции, заданные параметрически, и их производные.............….....……30

6.12.Дифференциалы высших порядков………………...…….….........….....……31

7.Теоремы о среднем…………………………………...............…..………………..…..32

7.1.Теоремы Ролля, Лагранжа, Коши…….…..……................…….…..………….32 7.2. Правило Лопиталя….…………...….……...……...............….….…..…………34 7.3. Формула Тейлора…….……..……….…………................….….…..…...….…36

8.Исследование функций с помощью производной…….......................…......…....…..40 8.1. Монотонность функции.….……..……………........….....……...…...………...40 8.2. Экстремумы функции…...……….....…………........…....……….….…….…..41 8.3. Наибольшее и наименьшее значения функции на отрезке….............……...43 8.4. Выпуклость и вогнутость. Точки перегиба……..….……….............…..…...44 8.5. Асимптоты графика функции………………….……………..............…..…...46 8.6. Схема исследования функции и построение ее графика….............…..….....48

9.Вектор-функция………………………...........………………………….….…..........50 10. Понятие функции нескольких переменных и ее производных..............................53

Библиографический список……………………………………………..................…..55

max{ 1 , 2 }

Глава 1. Предел и непрерывность функции одной переменной

Понятие предела является одним из важнейших понятий математического анализа. Основные понятия математического анализа, такие как производная, интеграл, связаны с предельным переходом.

Для сокращения записи мы будем использовать символы - любой и - существует. Запись x X : означает « для всякого элемента x X имеет место предложение ». Запись y Y : означает «существует элемент y Y , для которого имеет место предложение ». Запись означает « из предложенияследует предложение ». Запись означает, что и эквивалентны.

1. Определение предела

Для изучения пределов используются понятие окрестности точки.

1.1. Окрестности конечной точки и бесконечности

1). -окрестность конечной точки x0 обозначим S (x0 )

жество действительных чисел x R таких, что

x x0

S ( x0 ) {x R :

x x0

2). -окрестность бесконечности обозначим S ( )

и определим как множество действительных чисел

x R таких, что

(рис.2). Таким образом,

S ( ) {x R :

} .

3). -окрестность плюс бесконечности определим (рис.3) как

S ( ) {x R : x }.

4). -окрестность минус бесконечности определим (рис. 4) как

S ( ) {x R : x } .

5). Наряду с понятием окрестности введём понятие вы-

колотой окрестности S (x0 ) точки x0 , которая полу-

чается из окрестности S (x0 ) удалением точки x0 :

и определим как мно- (рис.1):

////////////////				x
x0 x0		x0
Рис.1			///////	x
////////		0

		Рис.2		x
0			////////

	Рис.3
/////////			0	x

Рис.4


S (x0 ) S (x0 ) \ {x0 } {x R : 0			x x0	}.	//////////////		x
Дополнительно будем полагать, что					2 1	a 1	2

S ( ) S ( ) ,	S ( ) S ( ) ,	S ( ) S ( ) .				Рис.5

6). Рассмотрим пересечение окрестностей.

Для конечной точки a имеем:

S 1 (a) S 2 (a) S (a), где min{ 1 , 2 } (рис 5).

В случае, если a , или a , или a , имеем:

S 1 (a) S 2 (a) S (a), где (рис. 6 для

///////// x

0 1 2

Рис.6

a ).

Аналогичным образом определяется и пересечение выколотых окрестностей.

1.2. Предел функции

Рассмотрим функцию f (x) и предположим, что аргумент x стремится к числу a (x a). Если для всех x, достаточно близких к a , соответствующие значения функции f (x) как угодно близки к числу b , то число b называют пре-

делом функции f (x) при x a ; записывают это следующим образом:

lim f (x) b.

x a

Требуется сделать ряд уточнений.

1). Выражение “значения f (x) как угодно близки к b ” означает, что значения f (x) попадают в произвольную -окрестность точки b , то есть f (x) S (b) для

любого 0 .

2). Выражение “ x , достаточно близких к a ” означает, что значения аргумента x

взяты из достаточно малой -окрестности a, то есть найдётся 0 такое, что x S (a) , причём для каждого 0 найдётся своё 0 , т.е. зависит от .

3). Функция f (x) может быть не определена в точке a , поэтому рассматриваются

значения x , близкие к a , но не равные a ,			то есть рассматриваются x из выколо-
той окрестности точки a . Например, функция				f (x)	x2 9	не определена при

					x 3
x 3 , но в выколотой окрестности точки x 3 (при x 3) имеем:
f (x)	(x 3) (x 3)	x 3 и	lim f (x) lim (x 3) 6 .

	x 3		x 3	x 3

С учетом этих уточнений дадим точное определение предела функции.

Число b называется пределом функции f (x) при x a , если для любого по-

ложительного числа найдётся положительное число	( ) такое, что значе-
ния функции f (x) принадлежат -окрестности точки b	для всех x	из выколо-
той -окрестности точки a.
Это определение распространяется и на случаи, когда a и (или)		b “несоб-

ственные числа”		, , . В дальнейшем это определение будем записывать
кратко с помощью символов следующим образом.


	lim f (x) b,	если для 0 0 такое, что	f (x) S (b)	для x S (a).
	x a

Рассмотрим более подробно несколько случаев.

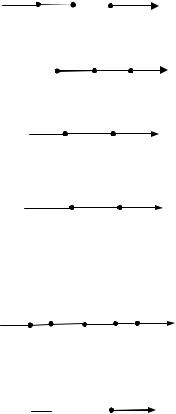
1). Пусть lim f (x) b, a и b – конечные числа (рис.7). Тогда


x a
f (x) S (b) означает, что	f x b		;
f (x) S (b) означает, что	f x b		;

x S (a) означает, что 0		x a	d
x S (a) означает, что 0		x a
и определение предела принимает вид:

b b b

a 2

a a 1


lim f (x) b,		если для 0		0 такое, что			Рис.7
x a							Рис.7
x a
	f x b		, как только	0	x a	.
	f x b		, как только	0	x a	.

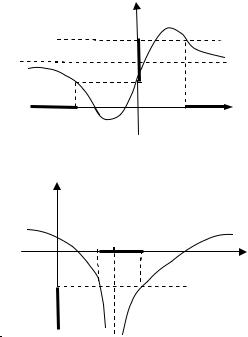
2). Пусть lim f (x) b,

b − конечное (рис.8). Тогда

f x b

f (x) S (b)

означает, что

;

x S ( ) означает, что

и определение предела принимает вид:

lim

f (x) b, если для 0

0 такое, что

как только

f (x) b

3). Пусть lim f ( x) ,

a конечное (рис.9). Тогда

x a

f x S означает, что

f (x) ;

x S (a) означает, что

x a

и определение предела принимает вид:

lim

f (x) , если для 0

0 такое, что

x a

f ( x)

, как только

x a

Другие возможные случаи (например a , b − конечное ; a b ) рассматриваются аналогично.

	y
	b
	b
	b
2	x
2	1
	Рис.8

a	a a
2	1
	x

Рис.9

1.3. Предел последовательности

Числовая последовательность – это значения un функции натурального аргумента f (n) , расположенные в порядке возрастания аргумента:

u1 f (1), u 2 f (2), … , u n f (n), …

Другое обозначение последовательности: Примеры последовательностей:


		1		1		1		1	n
1)		1		1		1		1		,
	1,		,		,		,	n
	1,	2	,		,		,
		2		3 4
									n 1

{u1, u2 , , un , } {un}n 1 .

	3			5		7
								2n 1
2)			,		,		,		.
		4		9		14		5n 1
									n 1

Предел последовательности можно рассматривать как частный случай предела

функции, а			именно функции натурального аргумента				f (n) u n	при n
(обычно пишут n ), т.е.

	lim u	n	b, если для 0	N 0 такое, что u	n	S	(b) для	n N.
	n	n			n

Если предел последовательности существует и конечен, то последовательность называют сходящейся. Если предел последовательности не существует или бес-

конечен,	то её называют расходящейся. Например, последовательность
u n ( 1)n	является расходящейся, так как члены последовательности с чётными
номерами	u 2n 1 , а	члены последовательности с нечётными номерами
u 2n 1 1	(n 1, 2, 3, ),	т.е. не существует числа, к которому бы неограниченно

приближались все члены последовательности по мере возрастания n .

Если функция имеет конечный предел при рой выколотой окрестности точки a .

1.4. Односторонние пределы функции

Пусть a конечное число. В определении предела функции аргумент x стремится к a любым способом: колеблясь около a , оставаясь меньше a или больше a . Иногда важен способ приближения x к a : слева (x a) или справа

(x a) . Тогда вводят понятие левостороннего предела

lim f (x)

и правосторон-

x a 0

него предела

lim f (x) следующим образом:

x a 0

если для 0

такое, что f (x) S (b)

для

lim

f (x) b,

x S (a),

x a;

x a 0

0 такое, что f (x) S (b)

lim

f (x) b, если для 0

для x S (a),

x a.

x a 0

Сформулируем очевидное утверждение:

lim f (x) b

lim f (x)

lim f (x) b.

x a

x a 0

Пример 1.1.

при x 0 .

Найти односторонние пределы функции

f (x)

Решение. При x 0 имеем:

f (x)

1 и, значит, lim f (x) 1.

x 0

При x 0 имеем: f (x)

и, значит,

lim f (x) 1.

x 0

Так как левосторонний и правосторонний пределы функции различны, то предел функции f (x) xx при x 0 не существует.

2. Теоремы о функциях, имеющих конечный предел

Пусть a число или один из символов , , .

Теорема 2.1 ( о единственности предела).

Если существует конечный предел функции при x a , то он единственен.

Доказательство этой и ряда других теорем не приводим.

Теорема 2.2 (об ограниченности функции, имеющей конечный предел).

x a , то она ограничена в некото-

Доказательство. Пусть существует конечный предел lim f (x) b . Тогда для

такое, что

. Отсюда

x a

f (x) b

f x

f x b b

f x b

для x S (a).

Это означает, что в выколотой окрестности S (a)

функция f (x) ограничена числом

Теорема 2.3 (о предельном переходе в неравенстве).

Пусть существует lim f (x) .

x a

Если f (x) c

в некоторой выколотой окрестности точки a , то

lim

f (x) c .

x a

Если f (x) c

в некоторой выколотой окрестности точки a , то

lim

f (x) c .

x a

Теорема 2.4 (о промежуточной функции).

Пусть lim

f (x) lim f

(x) b

и f (x) g(x) f

(x) в некоторой выколотой

x a

окрестности точки a.

Тогда

lim g(x) b .

x a

Теорема 2.5 ( о пределе суммы, произведения, частного).

Пусть существуют конечные пределы lim f (x)

и lim g(x) . Тогда

x a

lim [ f (x) g(x)] lim

f (x) lim g(x) ,

x a

lim [ f (x) g(x)] lim

f (x) lim g(x) ,

x a

lim [k g(x)] k lim g(x) ,

x a

f (x)

lim f (x)

lim

x a

если lim g(x) 0 .

x a g(x)

lim g(x)

x a

Доказательство проведем для одного из утверждений, например для первого.

Пусть lim f (x) b,

lim g(x) c ,

причем эти пределы конечны.

x a

Требуется доказать, что

lim [ f (x) g(x)] b c.

x a

Воспользуемся определением предела функции:

0 :

f ( x) b

для x S (a) ;

lim f (x) b для 0 , а значит, и для

x a

0 :

g(x) c

для x S 2 (a) .

lim g(x) c для 0 , а значит и для

x a

Два неравенства

f (x) b

g(x) c

выполняются одновременно в общей час-

. Поэтому для

ти двух окрестностей S (a) S 1 (a) S 2 (a)

x S (a) следует:

( f (x) g(x)) (b c)

f (x)

g(x) c

Это и означает, что lim [ f (x) g(x)] b c.

x a

Для формулировки теоремы о пределе элементарной функции отметим, что элементарная функция получается из основных элементарных функций (степенной, показательной, логарифмической, тригонометрической, обратных тригонометрических) с помощью арифметических операций и суперпозиции.

Теорема 2.6 (о пределе элементарной функции).

Пусть элементарная функция f (x) определена в точке x0 и ee окрестности.

Тогда lim f (x) f (x0) . x x0

Доказательство этой теоремы не приводим. Теорему нужно сначала доказать для основных элементарных функций, а затем воспользоваться теоремой 2.5. Для примера выберем из основных элементарных функций sin x и покажем, что

lim sin x sin x

sin x sin x

sin

x x0

cos

x x0

x x

x x 0

Следовательно, для 0

sin x sin x0

как только

x x0

Это и

означает, что

lim sin x sin x0 .

x x 0

Пример 2.1. Вычислить предел функции g(x)

x4 x3 lg x sin x 5

при x 1.

Решение. Функция g(x)

x2 2x 2

является элементарной и определена при x 1 . Поэтому

lim g(x) g(1)

или

lim

x3 lg x sin x 5

1 lg1 sin 5

x2 2x 2

1 2 2

x 1

Примеры для самостоятельного решения

1) lim

2) lim

sin x 3cos x

Найти пределы

x 3

x 7

x2 40

x 0

x 1

Ответы: 1)

2) 3.

3.Бесконечно малые функции

3.1.Определение и основные свойства

Функция f (x) называется бесконечно малой при x a , если lim	f (x) 0.
x a

Рассмотрим ряд свойств бесконечно малых функций.

Теорема 3.1 (о связи функции с ее конечным пределом).

lim f (x) b	f (x) b (x) , где ( x) бесконечно малая функция при x a .
x a
Доказательство. 1). Пусть lim f (x) b.			Рассмотрим функцию (x) f (x) b.
		x a
Вычислим ее предел: lim (x) lim [ f (x) b] lim				f (x) b b b 0 .
	x a	x a	x a
Так как lim (x) 0 , то (x)		есть бесконечно малая при x a и f x b x .
x a
2). В обратную сторону,		пусть f (x) b (x) ,		где ( x) бесконечно малая при
x a , т.е. lim (x) 0. Тогда lim f (x) lim [b (x)] b lim (x) b 0 b.
x a		x a	x a	x a

(x)

x a , а функция

Теорема 3.2 (о произведении бесконечно малой функции на ограниченную).

Пусть функция − бесконечно малая при f (x) − ограничена

внекоторой выколотой окрестности точки a . Тогда произведение этих функций

(x) f (x) является бесконечно малой при x a.

Доказательство. Функция f (x) ограничена в некоторой окрестности

S 1 (a) , т.е.

f (x)

для x S 1 (a) . Кроме того, функция ( x) бесконечно

малая при

x a , т.е.

lim (x) 0. Поэтому для 0 , а значит и для

найдется 2 0

x a

такое, что

(x)

для x S 2 (a) . Оба неравенства

f ( x)

M и

(x)

выполняются в окрестности S (a) S 1 (a) S 2 (a). Поэтому

( x) f ( x) (x) f (x)

для x S (a) .

Это и означает, что lim [ f (x) (x)] 0,

т.е. функция (x) f (x) является бесконеч-

x a

но малой при x a .

Пример 3.1. Будет ли бесконечно малой при x 0

функция f (x) x sin

Решение. Функция x является бесконечно малой при x 0 , а функция

sin

–

ограниченной в выколотой окрестности точки x 0 . Поэтому по теореме 3.2

функция f (x) x sin 1x является бесконечно малой при x 0 .

Теорема 3.3 (о сумме, разности, произведении бесконечно малых).

Сумма, разность, произведение конечного числа бесконечно малых при x a есть функция бесконечно малая при x a .

Доказательство. Пусть (x) и (x) бесконечно малые функции при x a , т.е.

lim (x) 0 и	lim (x) 0 .	Тогда
x a	x a
	lim [ (x) (x)] lim (x) lim (x) 0 0 0			,
	x a	x a	x a
	lim [ (x) (x)] lim (x) lim (x) 0 0 0 .
	x a	x a	x a
Это и означает, что функции (x) (x)			и (x) (x) являются бесконечно малыми

функциями при x a . Аналогично проводится доказательство для любого конечного числа бесконечно малых функций.

3.2. Отношение бесконечно малых. Неопределенность 0

Рассмотрим функции (x) x,

(x) x2 ,

3x ,

являющиеся бесконечно

малыми при x 0 . Так как

lim

(x)

lim

(x)

lim

x 0,

lim

(x)

3 ,

x 0 (x)

x 0

x 0 (x)

x 0

x 0 (x)

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.20152.64 Mб688Матанализ.doc
#
22.02.2015287.74 Кб31Матеем)).doc
#
22.07.2019118.27 Кб10Матезиус 6 (2).doc
#
22.02.2015523.22 Кб77матем статистика.docx
#
23.02.20154.87 Mб29Математика (Интегралы).rtf
#
13.03.20161.02 Mб26МАТЕМАТИКА 1 СЕМЕСТР АНАЛИЗ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.pdf
#
15.11.20192.66 Mб16математика 1 семестр.doc
#
23.02.201522.37 Кб13Математика и Физика экзамен.docx
#
23.02.20157.77 Mб11Математика методичка №2.pdf
#
23.02.20154.89 Mб52Математика производные и пределы.pdf
#
23.02.2015245.32 Кб13МАТЕМАТИКА Ч1.3 Практ.pdf