Паутинная модель рынка

Рассмотрим простейшую задачу поиска равновесной цены. Это одна из проблем рынка, так как стабильность рыночного равновесия позволяет определять границы целесообразности государственного вмешательства в рыночный механизм. Пусть сначала цену назначает производитель (в простейшей схеме он же и продавец). Ценана самом деле выше равновесной (всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спроспри этой цене и определяет свою цену, при которой этот спросравен предложению. Цена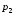ниже равновесной (всякий покупатель стремится купить подешевле). В свою очередь, производитель оценивает спрос, соответствующий цене, и определяет свою цену, при которой спрос равен предложению: эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к «скручиванию» спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену:(рис. 6.4).

Однако поиск равновесной цены не всегда приводит к «скручиванию» спирали. Кривые спроса и предложения могут иметь вид, отличающийся от кривых, описываемых уравнениями (6.1) и (6.2). Например, пусть предложение явно недостаточно и в формуле (6.2) , т. е., а покупательная способность населения чрезвычайна низка и в формуле (6.1). В этом случае процесс торга «раскручивает» спираль цен и уводит от(рис. 6.5).

6. Функция потребления и сбережения

Если х – национальный доход, – функция потребления (часть дохода, которая тратится), а– функция сбережения (сбережения населения), то. Дифференцируя, получим

,

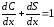где 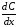– предельная склонность к потреблению;– предельная склонность к сбережению.

6.3. Эластичность функции и ее свойства

Пусть величина у зависит от х, и эта зависимость описывается функцией . Встает вопрос, как измерить чувствительность зависимой переменнойу к изменению х. Одним из показателей реагирования одной переменной на изменение другой служит производная. Однако в экономике этот показатель неудобен тем, что он зависит от выбора единиц измерения. Поэтому для измерения чувствительности изменения функции к изменению аргумента в экономике изучают связь не абсолютных переменных х и у, а их относительных изменений.

Определение. Эластичностью функции по аргументу в точке х называется предел отношения относительного изменения функции у к относительному изменению переменной х при :

.

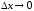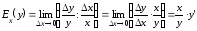Если эластичность представить в виде

,

то легко видеть, что она показывает приближенно, на сколько процентов изменится функция при изменении независимой переменной на 1%. Перепишем формулу эластичности в виде

,

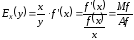где – маржинальное значение функции f в точке х, – среднее значение функции в точке х. То есть эластичность функции может быть представлена в виде отношения предельной () и средней () величин.

Так как , а, то эластичность можно представить в форме «логарифмической производной»

.

Геометрическая интерпретация эластичности

Эластичность функции можно найти из графика этой функции. По определению эластичности

,

где – угол наклона касательной к графику функции в точке(рис. 6.6) . Из треугольника. Треугольникии подобны, поэтому .

Т. е. эластичность возрастающей функции равна отношению расстояний по касательной от данной точки графика функции до точек ее пересечения с осями ординат и абсцисс. Если точкиилежат по одну сторону от точки, то, если по разные стороны, то .

Рассмотрим случай убывающей функции. . Так как треугольники иподобны, то, т. е. эластичность убывающей функции равна отношению расстояний по касательной от точки до точек ее пересечения с осями ординат и абсцисс, взятому со знаком минус (рис. 6.7).