10. 4. Двухфакторный дисперсионный анализ

Двухфакторный дисперсионный анализ (ДДА) служит для изучения влияния на результирующий признак двух различных факторов. ДДА подразумевает формирование и анализ двухфакторных дисперсионных комплексов (ДДК).

Анализ ДДК включает в себя 5 этапов.

1. Подбор факторов:

При организации ДДК свободный выбор факторов ограничен требованием их полной независимости друг от друга.

2. Разделение факторов на градации:

При организации ДДК каждый фактор разделяется на градации с таким расчетом, чтобы для каждой градации первого фактора было подобрано одинаковое число градаций второго фактора.

В качестве примера рассмотрим ситуацию, когда в качестве факторов выступают явно независимые друг от друга свойства, такие как пол и возраст (табл. 10.7).

Таблица 10.7

Факторы			Градации
А – пол			А1 - мужчины, А2 – женщины
В – возраст			В1 – 20 ¸ 30 лет; В2 – 30 ¸ 40 лет; В3 – 40 ¸ 50 лет;
Организация комплекса
Правильная							Неправильная
A1				A2			A1			A2
B1	B2	B3		B1	B2	B3	B1	B2	B3	B1	B2

3. Подбор объектов исследования:

Результаты дисперсионного анализа зависят от того, насколько правильно подобраны объекты исследования по качеству и по количеству.

По своему качеству объекты должны отражать те генеральные совокупности, для изучения которых проводится исследование.

По величине изучаемого признака объекты (испытуемые) должны быть взяты по принципу случайной выборки без учета выраженности данного признака. Измеряют и учитывают величину признака после отбора испытуемых в выборочный комплекс.

Организация дисперсионного комплекса с выполнением принципа случайности называется рандомизацией, а комплексы, организованные таким образом – рандомизированными. Нарушение принципа случайности при отборе объектов для дисперсионного анализа всегда приводит к неправильным результатам вследствие ошибки репрезентативности.

По числу объекты (испытуемые) могут быть распределены по градациям факторов различными способами - поровну, пропорционально или неравномерно. В соответствии с этим комплексы бывают равномерными, пропорциональными и неравномерными (табл. 10.8).

Таблица 10.8

Равномерные

Пропорциональные

Неравномерные

Гра-да-ции

A1

A2

Гра-да-ции

A1

A2

Гра-да-ции

A1

A2

B1

B2

B1

B2

B1

B2

B1

B2

B1

B2

B1

B2

N

15

15

15

15

n

5

15

10

30

n

10

10

10

30

B1:B2

1:1

1:1

B1:B2

1:3

1:3

B1:B2

1:1

1:3

В равномерных и пропорциональных комплексах отношение объемов градаций по второму фактору одинаково для каждой градации первого фактора. Такое распределение объектов по градациям ДДК определяет их особые ортогональные свойства. Комплексы, обладающие этими свойствами (равномерные и пропорциональные) называются ортогональными.

Работа с неравномерными комплексами достаточно трудна, а интерпретация результатов менее надежна, нежели при работе с ортогональными комплексами.

В некоторых случаях полученный неравномерный комплекс можно преобразовать в пропорциональный или равномерный рандомизированным изъятием отдельных единичных значений признака.

4. Преобразование значений результативного признака:

Для облегчения счетной работы можно неудобные для счета (или ввода в компьютер) значения результативного признака (многозначные, дробные) преобразовывать в малозначные и целые числа.

Возможны следующие преобразования:

1. Все значения признака можно разделить на одно и то же число К. Это делают тогда, когда все значения делятся на число без остатка, а также в случае перехода к новым единицам измерения. Если деление происходит без изменения единицы измерения, то в некоторые результаты надо внести соответствующие поправки: значения SS умножают на К², а Sx/n умножают на К.

2. Все значения можно умножить на одно и то же число К. Это делают, например, когда значения представлены дробными числами. Поправки в конечные результаты вносятся обратные тем, которые вносились в предыдущем случае.

3. От всех значений можно отнять одно и то же число А. Это лучше делать тогда, когда размах значений невелик и их деление или умножение на число К с последующим округлением может заметно снизить разнообразие измеряемого признака. Поправка в окончательный результат вносится только для среднего арифметического (необходимо прибавить числоА). Остальные значения никаких поправок не требуют.

4. Можно сделать двойное преобразование, например, из каждого значения можно вычесть число А, а полученный результат разделить (умножить) на число К.

Способы преобразования и поправки при различных типах преобразований показаны в табл. 10.9.

Таблица 10.9

Способ преобра­зования	Поправки
		SS
xi·K	: K	: K	: K	—	—
xi – А	+ A	—	—	—	—
(xi – A)/K	· K + A	· K2	· K2	—	—
xi/K	· K	· K2	· K2	—	—

Анализ двухфакторных комплексов

Анализ двухфакторных комплексов проводится в несколько этапов:

1. Расчет дисперсий (сумм квадратов). Дисперсии рассчитываются в трех однофакторных комплексах:

а) для общего комплекса (SS_b, SS_W, SS_C);

б) для первого фактора (А);

в) для второго фактора (В).

2. Анализ влияния. В ДДК анализируют 6 влияний:

а) влияние первого фактора (А);

б) влияние второго фактора (В);

в) влияние сочетаний градаций обоих факторов (АВ);

г) суммарное действие организованных (двух) факторов (А + В);

д) суммарное действие неорганизованных (остальных) факторов (случайные влияния) (W);

е) суммарное действие всех факторов, определяющих величину результирующего признака (C).

Все вышеперечисленные операции двухфакторного дисперсионного анализа можно проиллюстрировать следующим примером.

Условие задачи

На больных амнезией испытывалось действие двух лекарственных препаратов (А и В), которые, согласно предварительным испытаниям, способствуют улучшению памяти. Для первого препарата была взята контрольная группа (А₀) и группа больных, прошедших месячный курс лечения (А₁). Для второго препарата исследовались 3 градации больных (В₀ – контроль, В₁ – больные, прошедшие один курс лечения, и В₂ – больные, прошедшие два месячных курса лечения препаратом).

Для каждой комбинации были выбраны по 5 больных, которые тестировались по методу Эббингауза (запоминание и воспроизведение бессмысленных слогов). В качестве критерия использовалась средняя вероятность правильного воспроизведения у каждого больного. Получены следующие данные (табл. 10.10):

Таблица 10.10

Пациент	Комбинации
	A0B0	A0B1	A0B2	A0B0	A0B1	A0B2
1 2 3 4 5	0,08 0,22 0,32 0,20 0,12	0,80 0,64 0,96 0,72 0,80	0,56 0,42 0,56 0,46 0,32	0,24 0,36 0,48 0,36 0,72	0,16 0,22 0,28 0,42 0,56	0,32 0,16 0 0,16 0

Задание

Методом двухфакторного дисперсионного анализа определить степень эффективности препаратов А и В, используемых для лечения больных амнезией при их раздельном и совместном применении.

Решение

1. Используем операцию x_i·100:2. Получаем следующие данные (табл. 10.11):

Таблица 10.11

Пациент	A0B0	A0B1	A0B2	A0B0	A0B1	A0B2
1 2 3 4 5	4 11 16 10 6	40 32 48 36 40	28 21 28 23 16	12 18 24 18 36	8 11 14 21 28	16 8 0 8 0

2. Рассчитываем дисперсии в общем комплексе (табл. 10.12):

Таблица 10.12

	A0			A1
	Bo	B1	B2	B0	B1	B2
xi	4 11 16 10 6	40 32 48 36 40	28 21 28 23 16	12 18 24 18 36	8 11 14 21 28	16 8 0 8 0	JA = 2 JB = 3 n = 5
n	5	5	5	5	5	5	Jn = 30
	47	196	116	108	82	32
	442	7683	2691	2333	1345	205
	529	7824	2794	2664	1606	384
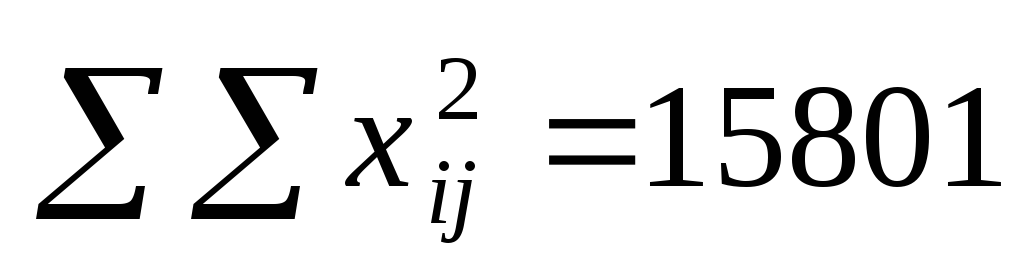
	9,4	39,2	23,2	21,6	16,4	6,4

а) межгрупповая дисперсия:

= 14699 – 11252 = 3447;

б) внутригрупповая дисперсия:

= 15801 – 14699 = 1102;

в) общая дисперсия:

= 15801 – 11252 = 4549.

3. Рассчитываем дисперсии для факторов А и В и для сочетания их градаций (АВ) (табл. 10.13):

Таблица 10.13

	Для фактора A			Для фактора B
	A0	A1	S	B0	B1	B2	S
n	15	15	30	10	10	10	30
	359	222	581	155	278	148	581
	8592	3286	11878	2402	7728	2190	12320

SS_A== 11878 – 11252 = 626;

SS_B== 12320 – 11252 = 1068;

SS_AB = SS_b –- SS_A – SS_B = 3447 – 626 – 1068 = 1753.

4. Проводим анализ частных средних:

А₀В₀ - контроль, А₁ - курс лечения препаратом А, В₁ - курс лечения препаратом В, В₂ - двойной курс лечения препаратом В.

А₀: В₀ = 9,4; B₁ = 39,2; B₂ = 23,2.

A₁: B₀ = 21,6; B₁ = 16,4; B₂ = 6,4.

Анализ частных средних показывает, что наиболее высокий уровень воспроизведения характерен для сочетания А₀В₁ (т.е. после месячного курса лечения препаратом В). Двойной курс лечения препаратом В нецелесообразен, т. к. воспроизведение снижается. Лечение препаратом А дает менее выраженный эффект, а комбинированное применение препаратов А и В вообще нецелесообразно

5. Анализ влияния(табл. 10.14).

Таблица 10.14

	SS		n	SS/n	F	n1 gAgB – 1	n2 Jn - gAgB	Fst b1; b2
A	626	0,14	1	626	13,61	1	24	4,3; 7,8
B	1068	0,23	2	534	11,61	2	24	3,4; 5,6
AB (n=nAnB)	1753	0,39	2	876	19,04	2	24	3,4; 5,6
A+B (n=gAgB-1)	3447	0,76	5	689	14,98	5	24	2,6; 3,9
W	1102	0,24	24	46
C	4549	1,00	29	157

Сила влияния:гдеSS_C - общая дисперсия.

Достоверность влияния:

:

где SS_W - случайная (внутригрупповая) дисперсия.

Анализ силы влияния

- действие первого фактора (при усредненном действии второго) составляет 0,14 (14%) от действия всей суммы факторов, определяющих величину результативного признака;

- действие второго фактора (при усредненном действии первого) оказалось более сильным: 0,23 (23%);

- значительно сильнее оказалось действие сочетаний градаций обоих факторов: 0,39 (39%);

- действие первого фактора в значительной степени зависит от градации второго: максимальный эффект наблюдается при отсутствии второго, минимальный - после двух курсов лечения вторым препаратом;

- в отсутствие первого фактора максимальный эффект наблюдается после одного курса лечения вторым препаратом, после повторного курса эффект снижается.

Анализ достоверности влияния

Влияние каждого из факторов в отдельности, а также их сочетания достоверно при 1-м (b₁ = 0,95) и 2-м (b₂ = 0,99) уровнях значимости.