6. 1. 5. Критерий Колмогорова – Смирнова (l)

Критерий Колмогорова – Смирнова основан на том же принципе, что и критерий χ² Пирсона, но предполагает сопоставление накопленных частот экспериментального и теоретического распределений. Вычисляется как отношение максимальной разности (без учета знака) между теоретической и экспериментальной накопленной частотой к корню квадратному из численности выборки: (6.6)

Для вычисления l также можно воспользоваться таблицами теоретических частот 8- и 16-классового распределения. Рассмотрим алгоритм вычислений критерия Колмогорова на примере предыдущей задачи (табл. 6.3).

Таблица 6.3

Границы класса	Экспериментальные частоты	Накопленные частоты		d
		Fэ	Fт
1	2	3	4	5
– 4 σ ÷ – 3 σ – 3 σ ÷ – 2 σ – 2 ÷ – σ – σ ÷ 0 0 ÷ σ σ ÷ 2 σ 2 ÷ 3 σ 3 ÷ 4 σ	0 2 16 34 30 17 1 0	0 2 18 52 82 99 100 100	0,13 2,28 15,87 50,00 84,13 97,72 99,87 100	0,13 0,28 2,13 2,00 2,13 1,28 0,13 0

Столбцы 1 и 2 аналогичны таковым в предыдущей таблице. Столбец 3 соответствует экспериментальным частотам, накопленным путем суммирования частот от 1-го до 8-го класса. Теоретические накопленные частоты взяты из табл. III Приложения. Максимальная разность между экспериментальной и теоретической накопленными частотами (столбец 5) соответствует 2,13. Проводим соответствующие вычисления:

Для определения соответствия экспериментального распределения теоретическому по критерию Колмогорова можно воспользоваться следующим правилом. Если l < 0,52, делается вывод о соответствии распределений для уровня значимости 0,95. При l > 1,36 распределение достоверно отличается от нормального. При значениях же l от 0,52 до 1,36 (интервал неопределенности) можно определить вероятность соответствия экспериментального распределения теоретическому по табл. VII Приложения.

Вывод

Полученное нами значение λ = 0,21 < 0,52, следовательно, по критерию Колмогорова экспериментальное распределение соответствует нормальному с вероятностью 0,95.

Для определения соответствия эмпирического распределения теоретическому (нормальному) распределению можно воспользоваться и другим способом, который зачастую дает более точные результаты, поскольку не ограничен числом классов. Этот способ будет нами рассмотрен на примере той же задачи.

Порядок вычислений приводится в табл. 6.4.

1. В столбце 1 таблицы фиксируем значения x_i (уровень нейротизма).

2. Переводим значения x_i в меру z Пирсона по формуле:

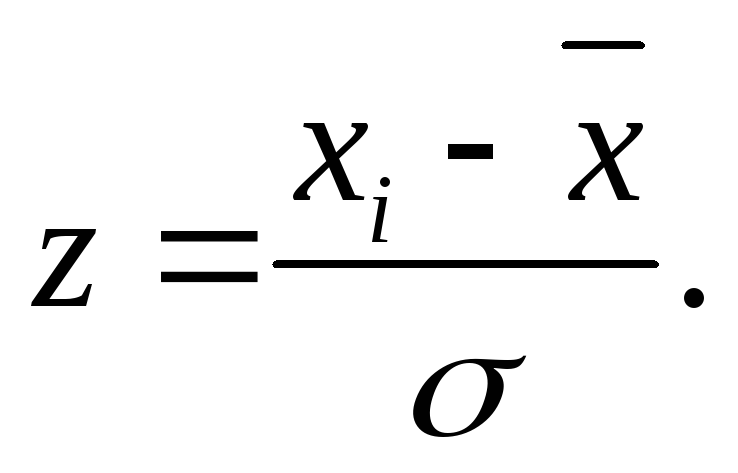
3. Ориентируясь на условие задачи, вносим экспериментальные частоты в столбец 3.

4. По значениям столбца 3 вычисляем накопленные экспериментальные частоты и фиксируем их в столбце 4.

5. По значениям z Пирсона определяем теоретические накопленные частоты, для чего используем табл. V Приложений.

6. Вычисляем критерий d, сравнивая между собой экспериментальные (столбец 4) и теоретические частоты по формуле: d = │F_эксп. – F_теор.│.

7. Вычисляем критерий λ Колмогорова по стандартной формуле.

Ответ

λ = 7,57:10 = 0,76 (столбец 6 таблицы), что соответствует интервалу неопределенности 0,52 ÷ 1,36.

С целью устранения случайных факторов используем процедуру интервальной нормализации (столбец 7) и повторно вычисляем критерий λ:

λ* = 4,64 : 10 = 0,46 (столбец 8 таблицы).

Общий ответ

Эмпирическое распределение соответствует теоретическому (нормальному) распределению.

Таблица 6.4

xi	Z	fэ	Fэ	Fт	d	Fэ*	d*
1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24	-3,2 -2,9 -2,7 -2,4 -2,2 -1,9 -1,6 -1,4 -1,1 -0,8 -0,6 -0,3 0 0,2 0,5 0,7 1,0 1,3 1,5 1,8 2,1 2,3 2,5 2,8	0 0 0 0 2 3 3 4 6 8 9 7 10 8 9 9 8 6 4 3 1 0 0 0	0 0 0 0 2 5 8 12 18 26 35 42 52 60 69 78 86 92 96 99 100 100 100 100	0,07 0,18 0,34 0,82 1,40 2,88 5,49 8,08 13,57 21,19 27,43 38,21 50,00 57,92 69,14 75,80 84,13 90,31 93,31 96,40 98,21 98,92 99,37 99,75	0,07 0,18 0,34 0,82 0,60 2,12 2,51 3,92 4,43 4,81 7,57 3,79 2,00 2,08 0,14 2,20 1,87 1,69 2,69 2,60 1,79 1,08 0,63 0,25	0 0 0 0 1 3,5 6,5 10 15 22 30,5 38,5 47 56 64,5 73,5 82 89 94 97,5 99,5 100 100 100	0,07 0,18 0,34 0,82 0,40 0,62 1,01 1,92 1,43 0,81 3,07 0,29 3,00 1,92 4,64 2,30 2,13 1,31 0,69 1,10 1,29 1,08 1,63 0,25