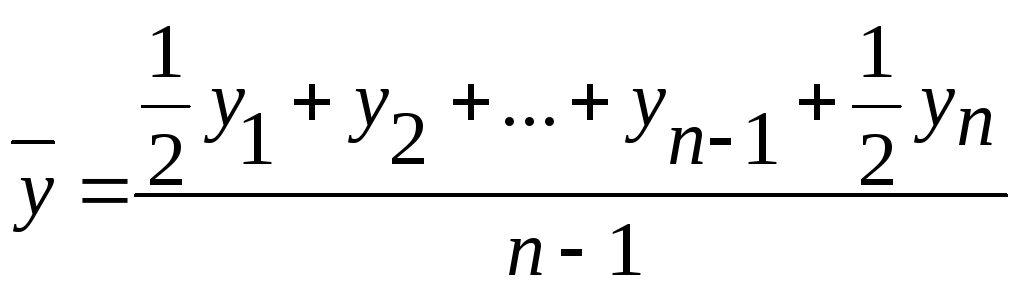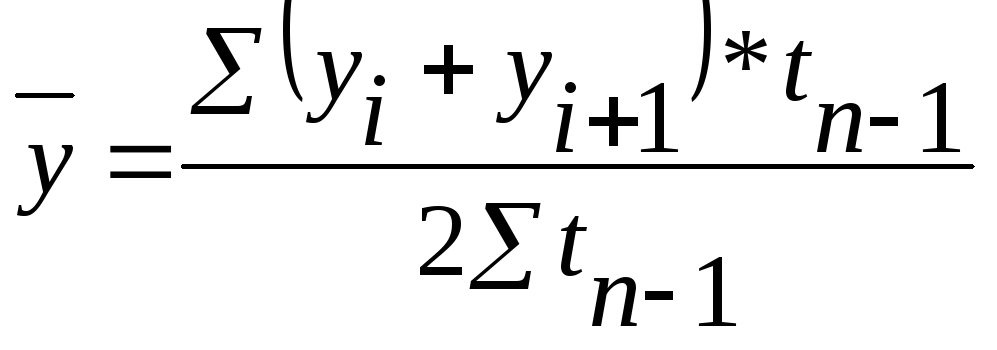- •080400 «Управление персоналом», профиль «Управление персоналом»
- •Пояснительная записка
- •2. Методические указания по выполнению контрольных работ
- •3. Контрольные задания в – 1 (для студентов, чьи фамилии начинаются с букв а, е, ж, р). Задача № 1
- •Задача № 2
- •Задача № 3
- •Задача № 4
- •Задача № 5
- •Задача № 1
- •Задача № 2
- •Задача № 2
- •В – 4 (для студентов, чьи фамилии начинаются с букв г, м, н, у, ш, ю). Задача № 1
- •Задача № 2
- •Задача № 3
- •Задача № 4
- •Задача № 5
- •В – 5 (для студентов, чьи фамилии начинаются с букв д, о, п, ф, щ, я). Задача № 1
- •Задача № 2
- •Задача № 3
- •Задача № 4
- •Задача № 5
- •4. Методические рекомендации по решению контрольных заданий
- •5. Список литературы
Задача № 2
Качество продукции предприятия характеризуется следующими данными (за месяц):
|
Вид продукции |
Процент брака |
Стоимость бракованной продукции, тыс. руб. |
|
А В С |
1,3 0,9 2,4 |
2135 3560 980 |
Определите средний процент брака в целом по предприятию.
Задача № 3
Из 200 ящиков по 100 деталей в каждом, поступивших на склад готовой продукции, в порядке случайной бесповторной выборки отобрано 5 ящиков, все детали которых проверены на вес. Результаты проверки следующие:
|
|
№ ящика | ||||
|
1 |
2 |
3 |
4 |
5 | |
|
Средний вес 1 детали, г. |
50 |
49 |
53 |
53 |
55 |
Определить: 1) возможные пределы среднего веса детали для всей партии, поступившей на склад (с вероятностью 0,954); 2) объем случайной бесповторной выборки, чтобы с вероятностью 0,683 предельная ошибка выборки при определении среднего веса одной детали для всей партии не превышала 0,7г.
Задача № 4
Известны темпы роста инвестиций за каждый год по двум регионам (в % к 2008г.):
|
Регион |
2009 |
2010 |
2011 |
|
А Б |
120 108 |
254 190 |
308 240 |
Определить темпы роста инвестиций за каждый год по сравнению с предшествующим годом и среднегодовые темпы роста инвестиций для каждого региона. Сформулируйте вывод.
Задача № 5
Имеются следующие данные о реализации молочных продуктов на городском рынке:
|
Продукт |
Товарооборот, тыс. руб. |
Изменение цены в декабре по сравнению с ноябрем, % | |
|
Ноябрь |
Декабрь | ||
|
Молоко Сметана Творог |
9,7 4,5 12,9 |
6,3 4,0 11,5 |
+2,1 +3,5 +4,2 |
Рассчитайте общие индексы цен, товарооборота и физического объёма реализации.
4. Методические рекомендации по решению контрольных заданий
Задача 1.
Данная задача решается с помощью метода группировок. Группировка – это разбиение совокупности на группы, однородные по какому – либо признаку. Этапы построения группировки:
1. Определение группировочного признака;
2. Определение числа групп;
3.
Определение интервала группировки
(если длина интервала не задана, то
определяем его по формуле для равных
интервалов:
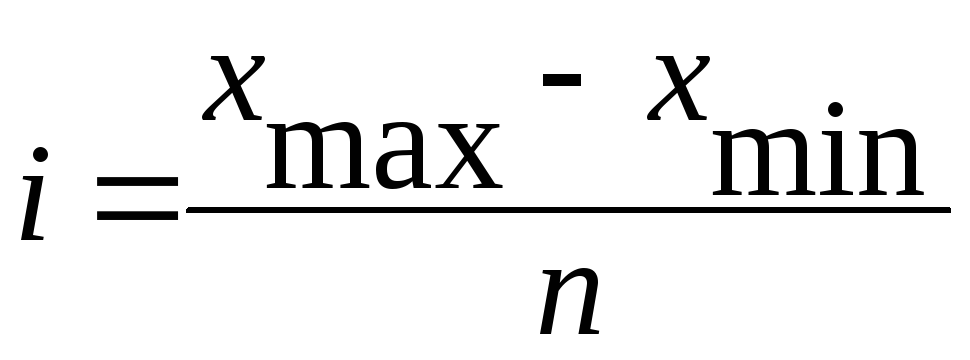 ,
где
i
– длина интервала,
,
где
i
– длина интервала,
![]() -
это максимальное, минимальное значение
признака у данной единицы совокупности; n
– число
групп);
-
это максимальное, минимальное значение
признака у данной единицы совокупности; n
– число
групп);
4. Разбиение совокупности на группы;
5. Оформление результатов в групповой таблице.
Задача 2.
Данная задача направлена на расчет средних величин. Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Виды средних величин:
1.
Средняя арифметическая простая
используется, когда известны варианты
(x),
имеющие равновеликие частоты (n)
–
![]() .
.
2.
Средняя арифметическая взвешенная
применяется, когда известны варианты,
имеющие неравновеликие частоты (f)
-![]() .
.
3.
Средняя гармоническая простая применяется,
когда вес каждого варианта равен единице
- 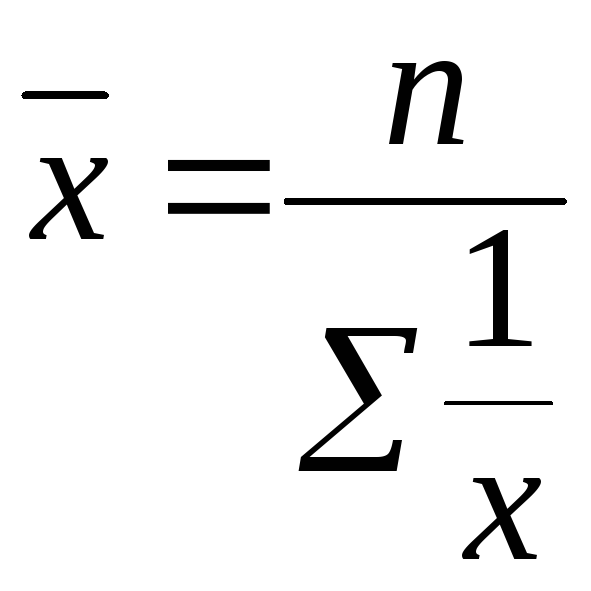 .
.
4.Средняя гармоническая
взвешенная применяется, когда неизвестны
веса, а имеется произведение варианты
на частоту -
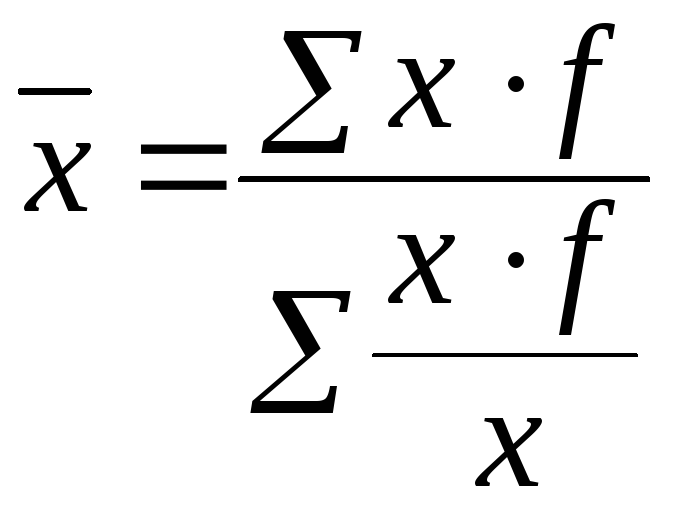 .
.
Задача 3.
Задание решается с помощью выборочного метода. Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю совокупность.
Для нахождения предельных ошибок выборки используются следующие формулы:
1. При повторном способе отбора:
- для средней количественного признака:
![]() , где
, где![]() -
выборочная дисперсия (дисперсия признака
в выборочной совокупности);n- объём выборки (число обследованных
единиц);
-
выборочная дисперсия (дисперсия признака
в выборочной совокупности);n- объём выборки (число обследованных
единиц);
t- где нормированное отклонение –
«коэффициент доверия», зависящий от
вероятности, с которой гарантируется
предельная ошибка выборки;![]() - средняя ошибка выборки.
- средняя ошибка выборки.
- для доли (альтернативного признака):
![]() ,
где- выборочная
доля (доля единиц, обладающих данным
признаком в выборочной совокупности);
,
где- выборочная
доля (доля единиц, обладающих данным
признаком в выборочной совокупности);
2. При бесповторном способе отбора
- для средней количественного признака
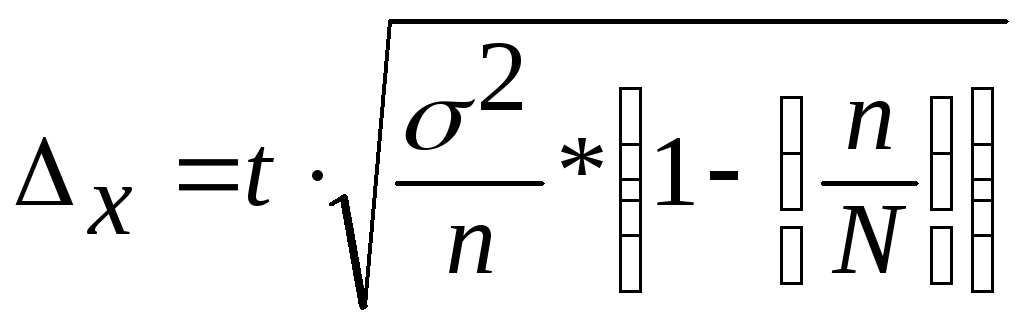 ,
гдеN -объем
генеральной совокупности (число входящих
в неё единиц);
,
гдеN -объем
генеральной совокупности (число входящих
в неё единиц);
- для доли (альтернативного признака)
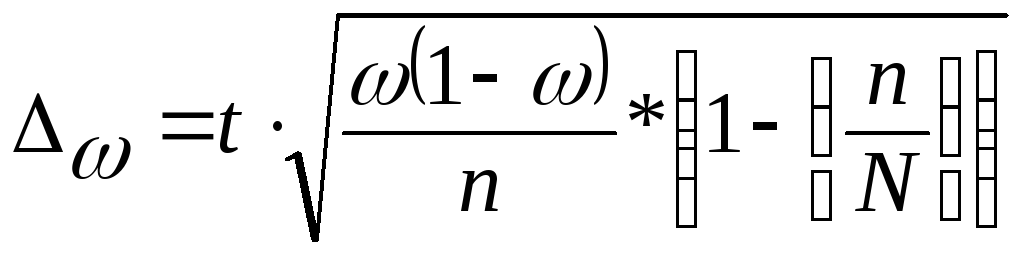 .
.![]()
Необходимый объём выборки определяется по формулам.
При бесповторном способе отбора:
- для
средней количественного признака
![]() ;
;
- для
доли (альтернативного признака)
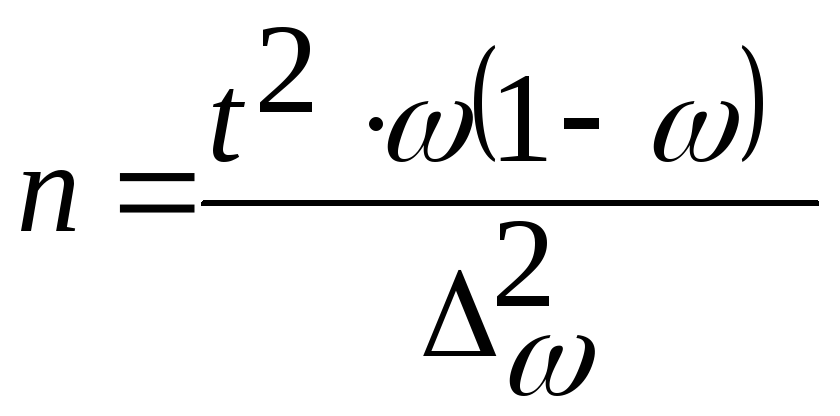 .
.
При повторном способе отбора:
- для
средней количественного признака
![]() ;
;
- для
доли
![]()
Задача 4.
Данная задача решается с помощь анализа рядов динамики. Формулы для расчета изменений от года к году следующие:
|
Наименование показателя |
Методы расчета | |
|
С переменной базой (цепные) |
С постоянной базой (базисные) | |
|
1. Абсолютный прирост (цеп; баз.)* |
цеп = yi – yi-1 |
баз = yi – y0 |
|
2. Коэффициент роста (Кр) |
|
|
|
3. Темп роста (Тр), % |
Трц = Kрц * 100 |
Трб = Крб * 100 |
|
4. Коэффициент прироста (Кпр) |
Кпрц = Kрц – 1
|
Кпрб = Крб – 1
|
|
5. Темп прироста (Тпр),% |
Тпрц = Кпрц * 100
|
Тпрб = Кпрб * 100
|
|
6. Абсолютное значение одного процента прироста (А%) |
|
|
Средние показатели за весь период определяются по формулам:
|
Наименование показателя |
Метод расчета |
|
1) Средний
уровень ряда ( а) для интервального ряда с: - равными интервалами
- неравными интервалами |
|
|
б) для моментного ряда с:
- равными интервалами
- неравными интервалами |
|
|
2) Средний
абсолютный прирост ( |
|
|
3) Средний
коэффициент роста ( |
|
|
4) Средний
темп роста (снижения) ( |
|
|
5) Средний
темп прироста ( |
|
|
6)Среднее
величина абсолютного значения 1%
прироста ( |
|
Задание 5.
Данная задача решается с помощью индексного метода.
Формулы для расчета:
![]() - общий индекс товарооборота,
- общий индекс товарооборота,
где p1 иp0– цены единицы продукции в отчетном и базисном периодах соответственно;
q1 иq0– количество продукции в отчетном и базисном периодах соответственно;
![]() - агрегатная форма общего индекса
физического объёма;
- агрегатная форма общего индекса
физического объёма;
![]() -
среднеарифметическая форма общего
индекса физического объёма, где
-
среднеарифметическая форма общего
индекса физического объёма, где
![]() -
индивидуальный индекс физического
объёма;
-
индивидуальный индекс физического
объёма;
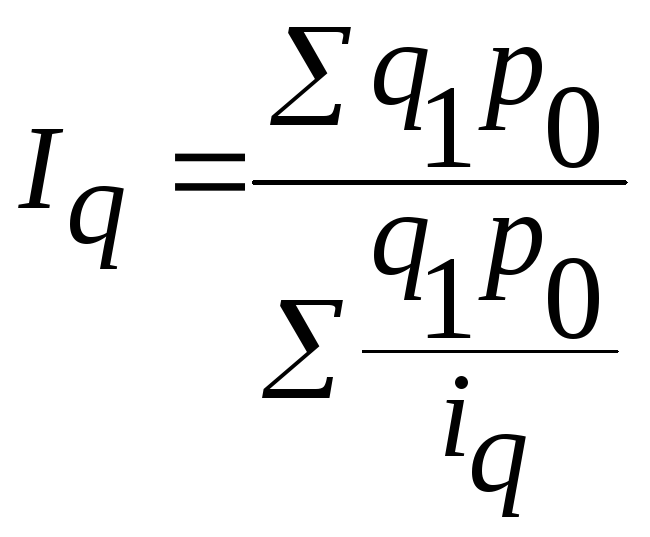 - среднегармоническая форма общего
индекса физического объёма;
- среднегармоническая форма общего
индекса физического объёма;
![]() - агрегатная форма общего индекса цен;
- агрегатная форма общего индекса цен;
![]() -
среднеарифметическая форма общего
индекса цен, где
-
среднеарифметическая форма общего
индекса цен, где
![]() -
индивидуальный индекс цен;
-
индивидуальный индекс цен;
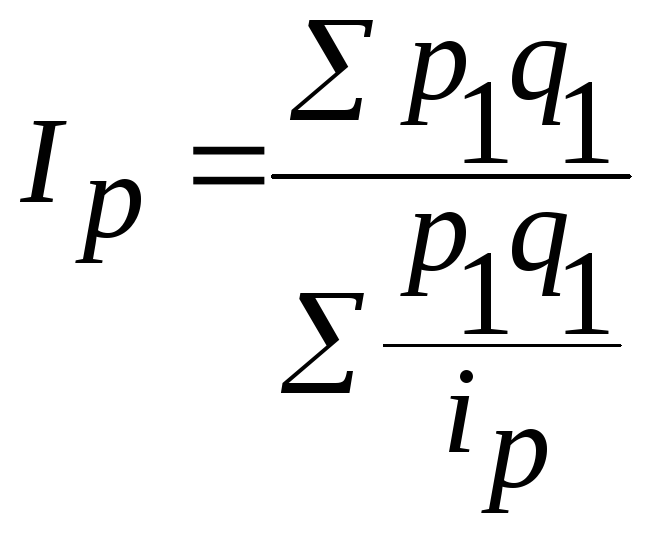 - среднегармоническая форма общего
индекса цен;
- среднегармоническая форма общего
индекса цен;
![]() -
агрегатная форма общего индекса
себестоимости продукции;
-
агрегатная форма общего индекса
себестоимости продукции;
![]() -
среднеарифметическая форма общего
индекса себестоимости продукции, где
-
среднеарифметическая форма общего
индекса себестоимости продукции, где
![]() -
индивидуальный индекс себестоимости
продукции;
-
индивидуальный индекс себестоимости
продукции;
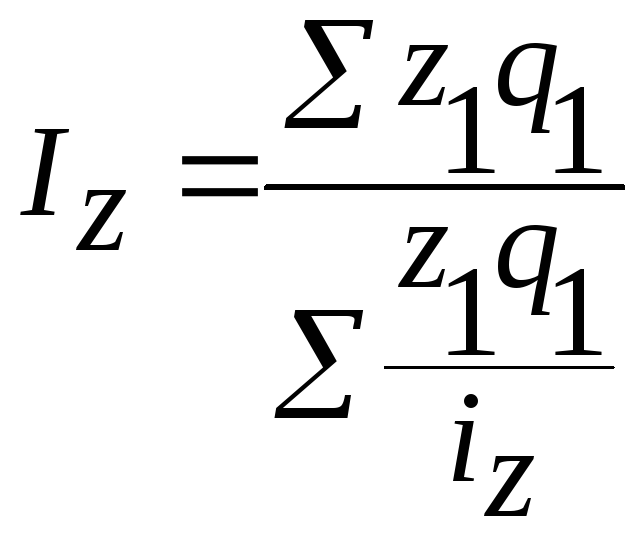 - среднегармоническая форма общего
индекса себестоимости продукции.
- среднегармоническая форма общего
индекса себестоимости продукции.