3. Показатели вариации.
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Т. о., величина каждого варианта объективна.
К показателям вариации относятся:
1. Размах вариации, представляющий собой разность между максимальным и минимальным значениями признака:
2. Среднее линейное
отклонение
представляет
собой среднюю арифметическую абсолютных
значений отклонений вариантов от их
средней арифметической ( при этом всегда
предполагают что среднюю вычитают из
варианта (x-
)).
Среднее линейное отклонение:
Для несгруппированых данных:
где n - число членов ряда;
для сгруппированных данных:
где
-
сумма частот вариационного ряда.
3.Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины. Она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
простая дисперсия для несгруппированных данных
взвешенная дисперсия для вариационного ряда
4. Среднее
квадратическое отклонение
равно
корню квадратному из дисперсии:
для несгруппированных
данных
для вариационного
ряда
.
5. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к среднеарифметической:
Коэффициент вариации используется не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.
Вариация альтернативного признака.
Статистическое
изучение вариации многих
социально-экономических явлений
проводится и при помощи дисперсии
альтернативного признака, т. е. признаков,
которыми одни единицы обладают и не
обладают другие. Обозначим наличие
данного признака 1, отсутствие 0, долю
вариантов, обладающим данным признаком
p, а не обладающих имq. Т. к. рядp+q= 1, то средняя
(
),
а дисперсия признака
,
.
Подставив в формулу дисперсииq
= 1 - p,получим
,
гдеp =
,n– число наблюдений,m– число единиц совокупности, обладающих
данным признаком.
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсий.
Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обуславливающих эту вариацию:
.
Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака – фактора, положенного в основание группировки. Она рассчитывается по формуле:
.
Внутригрупповая дисперсия отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака – фактора, положенного в основание группировки. Она исчисляется следующим образом:
- простая;
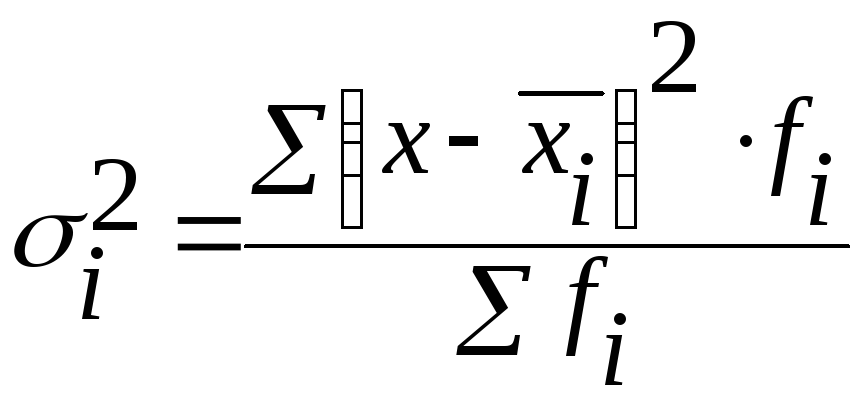- взвешенная.
На основании
внутригрупповой дисперсии по каждой
группе, т. е. на основании
можно
определить среднюю из внутренних
дисперсий:
.
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
.
На основании правила сложения дисперсий можно определить показатели тесноты связи между группировочным и результативным признаками:
1. Эмпирический коэффициент детерминации - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
.
2. Эмпирическое корреляционное отношение это показатель тесноты связи между группировочным и результативным признаками.
Если
:
0,1-0,3 – связь слабая;
0,3-0,5 – связь умеренная;
0,5-0,7 – связь заметная;
0,7-0,9 – связь тесная;
0,9-0,99 – связь весьма тесная.