
Arifm_ustr
.pdfМинистерство образования и науки Российской Федерации Федеральное агентство по образованию
Федеральное образовательное учреждение высшего профессионального образования «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
__________________________________________________________________
Г.И. КУЛЕШОВ
ЦИФРОВЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ
АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
СХЕМЫ ВЫЧИТАНИЯ ДВОИЧНЫХ ЧИСЕЛ
Метод сведения вычитания к сложению
Вычитание двух чисел сводится к операции сложения. Разность D
уменьшаемого A и вычитаемого B можно записать в виде |
|
D A B A (C B) C . |
(1) |
При этом следует С выбрать таким образом, чтобы операция C B (вычис-
ление дополнения В до С), так же как и вычитание С, проводилась без помощи специальных схем, реализующих вычитание. В случае N-разрядных двоичных
чисел AN |
и ВN это возможно как при C 2N , так и при C 2N 1. Если |
|
C 2N , |
то выражение C B |
называется точным двоичным дополнением |
|
N |
|
B(2) , а если C 2N 1, то поразрядным дополнением B(1) . Запись числа с |
||
N |
|
N |
помощью его точного двоичного дополнения называется также дополнитель-
ным кодом, а с помощью поразрядного дополнения – обратным кодом.
Из соотношений
|
B(2) |
2N B |
|
(2) |
|
N |
N |
|
|
и |
B(1) |
2N 1 B |
|
(3) |
|
N |
N |
|
|
следует, что |
|
|
||
|
B(2) |
B(1) 1 . |
|
(4) |
|
N |
N |
|
|
Поразрядное дополнение |
B(1) |
получается просто путем инвертирования всех |
||
|
|
|
N |
|
разрядов числа ВN. Справедливость этого утверждения вытекает из того, что максимальное число, которое можно записать в двоичном .N-разрядном коде,
равно 1111... =2N–1.
Следовательно, вычитая из этой величины любое двоичное число ВN с целью
2
определения его дополнения BN(1) , мы непременно получим то же двоичное число, которое составляется путем инверсии всех разрядов ВN. Получение до-
полнения BN(2) несколько сложнее, так как после инвертирования всех разря-
дов ВN к полученному результату следует еще прибавить 1.
Рассмотрим операцию вычитания в случае поразрядного дополнения. При C 2N 1 получим
A B A (2N |
1 B ) (2N 1) |
|
||
N |
N |
N |
N |
(5) |
A |
B(1) |
2N 1. |
|
|
|
|
|||
N |
N |
|
|
|
Таким образом, вычитание можно осуществить, инвертируя число ВN, прибав-
ляя еще одну единицу и вычитая 2N . Вычитание 2N достигается весьма про-
сто – путем инверсии разряда переноса. Для добавления 1 на свободный вход сигнала переноса с0 можно подать единицу. Поэтому здесь не требуется допол-
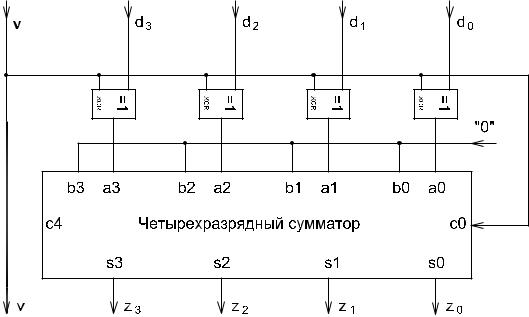
нительных суммирующих цепей. При этом получается схема, представленная на рис. 1.
Рассмотрим теперь случай точного двоичного дополнения (C 2N ). Для него можно записать
A B A (2N B ) 2N |
|
||||
N |
N |
N |
N |
(6) |
|
A |
B(2) |
|
2N. |
||
|
|||||
N |
N |
|
|
|
|
Если вычитаемое число ВN уже задано в форме двоичного дополнения, то чис-
ла АN и BN(2) можно складывать с помощью обычной суммирующей схемы,
инвертируя при этом разряд переноса. Однако, если ВN является обычным по-
ложительным числом, необходимо предварительно вычислить его двоичное
3

|
|
|
|
Рис. 1. Схема вычитания двоичных чисел |
||
дополнение |
|
B(2) |
по поразрядному дополнению |
B(1) |
, пользуясь формулой (4). |
|
|
|
N |
|
|
N |
|
Тогда, согласно соотношению (6), получим |
|
|
||||
A B |
A |
|
B(1) 1 2N , |
|
(7) |
|
N |
N |
N |
N |
|
|
|
что полностью совпадает с (5). При этом получается та же схема, что и на рис. 1. Различие между этими двумя способами вычитания состоит только в
моменте прибавления единицы. При поразрядном дополнении оно выполняется после суммирования AN и ВN, а при двоичном – до него. Однако в случае ис-
пользования сумматоров комбинационного типа это различие несущественно.
Арифметические устройства, выпускаемые промышленностью, часто име-
ют встроенные элементы для инвертирования ВN . Они производят операцию инвертирования при подаче соответствующего управляющего сигнала. Более простые схемы сумматоров могут иметь дополнительные входы с инвертирова-
нием, для выбора используемых входов в этом случае требуется применение внешних коммутаторов.
Рассмотрим теперь случай, когда искомая разность DN отрицательна. При этом в разряде переноса появляется 1. Она может рассматриваться, как разряд числа в весом 2N и знаком минус (отрицательный перенос –2N ). Поясним это на примере, представленном в таблице 1. Итак, разность можно записать в виде
4

DN 2N ZN . При изменении порядка вычитания отсюда следует
D |
|
2N Z |
N |
. |
|
||||
N |
|
|
|
Таблица 1 Пример представления разности при положительном и отрицатель-
ном результатах вычитания
Двоичное |
Десятичное |
|
Двоичное |
Десятичное |
число |
число |
|
число |
число |
1010 |
10 |
|
1000 |
8 |
–1000 |
–8 |
|
–1010 |
–10 |
[0] 0010 |
2 |
|
[1] 1110 |
–2 |
|
|
|
ZN |
|
Таким образом, введенное число ZN представляет собой точное двоичное до-
полнение модуля разности. При продолжении арифметических операций такое представление является весьма удобным. Однако для оценки результата часто необходимо иметь его величину в обычном двоичном (прямом) коде и его знак.
Представление результата вычитания в виде модуля числа и знака
Для разделения разности на модуль и знак при появлении единицы в разряде переноса v следует вычислить двоичное дополнение числа DN , что достига-
ется с помощью N управляемых инверторов, которые можно реализовать с по-
мощью элементов ―ИСКЛЮЧАЮЩЕЕ ИЛИ‖. Но из-за необходимости при-
бавления 1 требуется еще одна дополнительная суммирующая схема, показан-
ная на рис. 2. В зависимости от знака разности проводятся преобразования
D |
v 0; |
Z N |
|
2N DN DN(2) , |
v 1. |
При выполнении операций с поразрядным дополнением можно исключить вто-
рую суммирующую схему. Для доказательства этого вернемся еще раз к урав-
нению (1) и запишем в общем виде модуль отрицательной разности DN :
5
| D | D [C D] C при D 0. С учетом (1) отсюда получим
| D | C [ A (C B) C] C ,
(8)
| D | C [ A (C B)].
Рис. 2 Формирование двоичного дополнения числа в зависимости от его знака
В отличие от ранее рассмотренного случая положительной разности здесь два корректирующих члена C 2N или C 2N 1 взаимно уничтожаются. Та-
ким образом, если оперировать поразрядным дополнением, то 1 два раза не прибавляется. При этом можно записать | D | [ A B(1) ](1) .
Чтобы результат автоматически разделить на знак и модуль, необходимо снача-
ла подать числа A и B(1) на суммирующую схему и проанализировать полу-
ченный при этом неинвертированный сигнал c4 . Если он равен единице, то разность положительна. В этом случае, как уже было показано, необходимо прибавить 1, для чего следует положить с0 = 1. Это очень просто осуществить,
6
подключая старший сигнал переноса к с0. Такая схема называется схемой цик-
лического переноса.
Если старший сигнал переноса равен нулю, то полученная разность отрица-
тельна. В этом случае прибавление 1 автоматически блокируется. При этом нужно еще проинвертировать результат, что дает модуль разности.
Теперь остановимся на особом случае, когда А = В . Тогда на входы всех разрядов сумматора подается комбинация сигналов 01, т. е. функция распро-
странения переноса рассматриваемой секции Р равна 1. Поэтому с4 = с0 и в схеме образуется положительная обратная связь, т.е. нельзя заранее предуга-
дать, получится в результате плюс ноль (+ 0) или минус ноль ( – 0).
Эти трудности легко обойти, если использовать суммирующую схему с параллельным переносом. Как показано на рис. 3, цепь циклического перено-
са можно подключить не к выходу переноса с4, а к выходу функции генерации переноса G. Как следует из выражения (2.3), величина функции совпадает с
с4 , если не принимать во внимание величину с0. Таким образом устраняется причина образования положительной обратной связи. С другой стороны, сигнал
G достаточен для определения знака, поскольку сигнал с4 при прибавлении единицы не изменяется. Незначительный недостаток этого способа состоит в том, что нуль выдается как отрицательное число. Это, вообще говоря, не явля-
ется ошибкой, но не всегда приемлемо. Для устранения этого эффекта при
A = В следует организовать еще один дополнительный циклический перенос и запретить образование дополнения на выходе. С этой целью сигнал распро-
странения переноса Р с помощью элемента ―ИЛИ‖ также подключен к цепи циклического переноса. Выполняются следующие операции:
|
0, |
A B |
|
D | A B | ; |
v |
A B |
. |
|
1, |
|
Принципиальная схема устройства приведена на рис. 3.
7
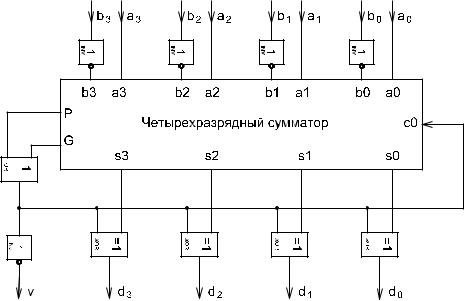
Рис. 3 Вычитание двух двоичных четырехразрядных чисел с вычислением аб-
солютной величины и знака разности по методу циклического переноса
Сложение чисел с любыми знаками
Запись N-разрядного числа в двоичной позиционной системе счисления имеет вид полинома
N 1 |
|
|
Z 2 j z j |
2N 1 zN 1 2N 2 zN 2 21 z1 20 z0 . |
(9) |
j 0
Рассмотрим на множестве целых чисел часто применяемое представление чи-
сел со знаком в двоично-дополнительном коде. В нем используемый для коди-
рования знака крайний левый разряд zN-1 рассматривается, как старший, име-
ющий наибольший вес, и отрицательный знак. Для положительных чисел зна-
ковый разряд равен 0, для отрицательных чисел он равен 1. Представление по-
ложительных чисел в соответствии с (9) совпадает с рядом натуральных двоич-
ных чисел, отрицательные числа получаются в результате сложения знака и остальной части числа. При инвертировании знакового разряда все числа ста-
новятся положительными, увеличиваясь на 2N-1 . Эта операция называется
8
сдвигом двоичного представления. Такое представление используется преиму-
щественно при выполнении операций со знакопеременными числами (пред-
ставление чисел в форме двоичного дополнения).
Схема вычитания, представленная на рис. 1, в случае отрицательной раз-
ности выдает ее значение в форме двоичного дополнения. Старший разряд пе-
реноса v можно рассматривать при этом непосредственно как знак: v = 0
означает положительный результат, v = 1 – отрицательный. Таким образом,
схема вычитания формирует значение отрицательной разности в двоично-
дополнительном коде. Для 8-разрядного числа имеется область определения от минус 128 до плюс 127, как показано в таблице 2.
Таблица 2 Область определения 8-разрядных двоичных чисел
v |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
b7 |
b6 |
b5 |
b4 |
b3 |
b2 |
b1 |
b0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
+127 = 0+127 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
+1 = 0 + 1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
= 0 + 0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
–1 |
= –128 + 127 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
–2 |
= –128 + 126 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
–128 |
= –128 + 0 |
|
|
|
|
|
|
|
|
|
|
Такое представление чисел объясняется тем, что знаковый разряд с можно рас-
сматривать как обычный двоичный разряд определенного веса, взятый, однако,
с отрицательным знаком. В случае 8-разрядного положительного числа В8
старший разряд v = b7 |
= 0, и получим B b |
27 B |
B 0. |
|||||
|
|
|
|
|
8 |
7 |
7 |
7 |
В случае отрицательного 8-разрядного числа В8 |
старший разряд v = b7 = 1, и |
|||||||
получим |
B b 27 |
B 27 |
B 0. |
|
|
|
||
|
|
8 |
7 |
7 |
7 |
|
|
|
Модуль В8 |
в этом случае равен |
|
|
|
|
|||
| B | B |
27 |
B B(2) 0, |
|
|
|
|
||
8 |
8 |
|
7 |
7 |
|
|
|
|
9
т. е. представляет собой точное двоичное дополнение В7 .
Рассмотрим теперь, как должна работать суммирующая схема, чтобы правильно оперировать с положительными и отрицательными числами, пред-
ставленными в форме двоичного дополнения. В соответствии с приведенным выше примером рассмотрим суммирование двух чисел А и В , разрядность ко-
торых составляет; 7 бит плюс знаковый разряд v. Суммирующая схема реали-
зует выражение S7 A7 B7 .
Рассмотрим сначала случай А >0, В > 0 . Эти числа складываются со-
вершенно правильно. В отличие от сумматора, предназначенного только для положительных чисел, имеется одно ограничение: так как теперь восьмой дво-
ичный разряд рассматривается как знак, его уже нельзя использовать как разряд переноса. Поэтому сумма не должна выходить за пределы 7-разрядного числа.
Следовательно, она не может быть более 27 — 1 = 127, так как в противном случае результат будет ошибочно рассматриваться, как отрицательное число.
Случай, когда одно из двух чисел (А7 или В7) задано в форме двоичного до-
полнения, уже рассматривался выше, поскольку там вычитание было заменено на сложение с. двоичным дополнением вычитаемого. Чтобы получить правиль-
ное значение знака разности, разряд переноса инвертировался. Так как числа А и В равноправны, сигнал переноса необходимо инвертировать всегда, когда либо А, либо В отрицательно.
Кроме того, может встретиться случай, когда и А, и В – отрицательны.
Сумма двоичных дополнений составит
S7 A7(2) B7(2) 27 A7 27 B7
28 A7 B7 .
Очевидно, что вследствие сложения двух членов дополнений, равных 27,
разряд переноса (восьмой двоичный разряд) b7 не изменится; следовательно, в
нем непосредственно появится знак. Все рассмотренные комбинации представ-
10
