
Reactive Intermediate Chemistry
.pdf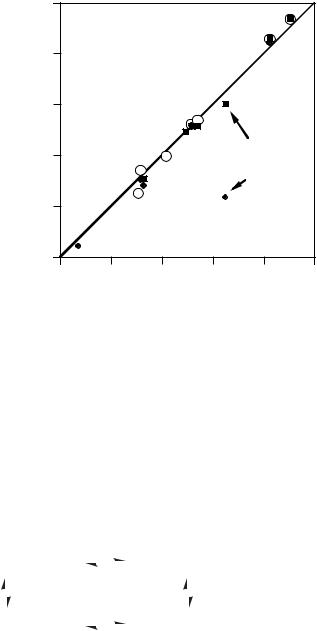
BASICITY OF CARBANIONS–ACIDITY OF CARBON ACIDS |
91 |
pK (ion pair)
35
30
25
20
p-Ph−PhC(O)i-Pr
15
10
10 |
15 |
20 |
25 |
30 |
35 |
pKa (DMSO)
Figure 3.2. Plot of ion-pair acidities in THF131–133 and CHA125 versus free ion values in DMSO.38 Filled squares are for cesium ion pairs and filled diamonds are for lithium ion pairs in THF. Open circles are for cesium ion pairs in CHA. For convenience, a line with slope ¼ 1 and intercept ¼ 0 has been placed on the plot.
ion-pair acidities for this compound in its monomeric form. The cesium ion-pair acidity [pKCs(THF) ¼ 25.08] matches the DMSO pKa value of a simpler analogue, phenyl isopropyl ketone (pKa ¼ 26:25), but the lithium ion-pair acidity is much lower [pKLi(THF) ¼ 15.88]. The difference between the ion-pair acidities in THF and free ion acidities in DMSO can be analyzed with the following set of linked equilibria suggested by Streitwieser and co-workers133 (Scheme 3.3).
|
– |
M + + R |
|
|
|
KIP |
|
|
M+ |
|
|
|
|||||||
R |
2 |
H |
|
|
|
R H + R – |
Kd |
|
|
||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KIP = |
1 |
K FI |
|
|
|
|
Kd |
1 |
|
|
|
|
|
|
|
|
Kd |
2 |
Kd |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
KFI |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R – |
|
+ M+ + R2H |
|
|
– |
|
+ M+ |
|
|
|
|||||||||
|
|
|
|
R H + R |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
Scheme 3.3
If ion-pair dissociation constants, Kd1 and Kd2, are roughly the same, which tends to be true for hydrocarbons, then the ion-pair KIP and true, free-ion KFI values will be
92 CARBANIONS
approximately equal. This factor is why such a good correlation is seen in Figure 3.2 for the hydrocarbon species. Although the Kd values for the lithium and cesium salts of hydrocarbon-derived carbanions are different in THF,133 the lithium values are uniformly 100 times larger due to the stronger interaction of the cation with THF. This effect cancels out when both scales are arbitrarily referenced to the DMSO value for fluorene (22.9 on a per hydrogen basis). Note that the situation is somewhat more complicated in THF because two types of ion pairs are formed, contact ion and solvent-separated ion pairs. In the former, the cation directly interacts with the carbanion whereas in the later, the cation is fully solvated and it is the cation–solvent complex that interacts with the carbanion. Cesium generally prefers contact ion pairs, but lithium prefers solvent-separated ion pairs with delocalized hydrocarbon carbanions because it allows for strong electrostatic interactions of the lithium cation with the oxygens of THF.
For an ion-pair acidity value to differ significantly from the free-ion value, Scheme 3.3 indicates that there must be a large difference between Kd1 and Kd2. In other words, the species of interest must have an ion-pair dissociation constant that is very different from the reference hydrocarbon used in the measurement (R1H). For example, when R2 is an enolate, Kd2 will be very small for lithium because there will be a strong electrostatic interaction with the highly charged oxygen of the enolate and the salt will resist dissociation. As a result, KIP will be unusually large and the parent acid, R2H, will appear to be unusually acidic under the ion-pairing conditions. The 9.2 pK difference between the lithium and cesium ion-pair acidities of p-biphenyl isopropyl ketone indicates that the formation of the lithium ion pair (relative to the cesium ion pair) provides roughly nine orders of magnitude of stabilization to the enolate. This is an overstatement of the true effect because lithium has a higher dissociation constant than cesium with the hydrocarbon reference species, but it still implies that Kd is nearly 10 million times smaller for lithium cations than cesium cations with this enolate. Obviously, there is a very strong electrostatic interaction between the small, densely charged lithium cation and the oxygen of the enolate (in this case, the lithium must be adopting a contact ion pair). The large cesium cation doesn’t offer the high charge density of the lithium cation and therefore ion-pairing has little effect on the stability of the enolate relative to the delocalized carbanions used to develop the acidity scale (i.e., those that fit the correlation line in Figure 3.2), and hence the cesium ion-pair pK is close to the DMSO value.
Finally, it is worth noting that large differences in acidity can occur in switching to solvents capable of hydrogen bonding. As expected, the effect is closely related to nature of the atom bearing the bulk of the charge in the anion. Cox and Stewart134 developed an acidity function that uses data in aqueous DMSO mixtures to extrapolate to a dilute aqueous reference state. With this approach, the pKa of fluorene is nearly the same as in pure DMSO (22.1 vs. 22.6). However, acetone’s pK value is >6 units lower in aqueous solution100 than DMSO. Clearly, the localization of charge on the oxygen is allowing the acetone enolate to benefit more from the access to hydrogen bonding and it is greatly stabilized by the solvent relative to a delocalized carbanion derived from a hydrocarbon. Nitroalkanes also exhibit

BASICITY OF CARBANIONS–ACIDITY OF CARBON ACIDS |
93 |
large pKa shifts in going to hydrogen-bonding solvents due to the importance of a resonance form where the anion’s charge is carried by the oxygens.38
4.3.3. Gas-Phase versus Condensed-Phase Acidities. As noted above, in the absence of strong interactions with a counterion or hydrogen bonding, carbon acidities are relatively insensitive to the solvent. As a result, one expects, at least for hydrocarbons, that there would be a good correlation between gasand condensedphase acidities. Taft and Bordwell135 compared data from the gas phase and DMSO and presented several conclusions about solvation effects. First, for hydrocarbons that give delocalized carbanions, there is an excellent correlation between the gas-phase and DMSO data, with nearly a 1:1 correspondence in the relative free energies of deprotonation—of course, the absolute free energies of deprotonation are much higher in the gas phase. A sample of such data is presented in Figure 3.3. Here, the linear fit has a slope of 1.026 and a correlation coefficient r2 value of 0.980. Second, the addition of fused benzene rings to a cyclopentadiene core clearly reduces acidity in solution, but has little effect in the gas phase (see Fig. 3.1 for structures). In terms of relative free energies of deprotonation, DMSO yields the ordering cyclopentadiene (0.0 kcal mol 1) < indene (2.9 kcal/ mol) < fluorene (6.3 kcal/mol). In contrast, the gas-phase values are reversed and
Gas Phase ∆G (kcal/mol)
y = 1.026x + 310.447 r 2 = 0.980
360
triphenylmethane
355
diphenylmethane
350
345
fluorene
340
335 |
|
|
|
9-phenylfluorene |
|
|
|
330
1,3-diphenylindene
325
fluoradene
320
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
DMSO ∆G (kcal/mol)
Figure 3.3. Plot of gas-phase free energies of deprotonation54 versus those found in DMSO.135

94 CARBANIONS
closer together with cyclopentadiene (0.0 kcal/mol) > indene ( 3.1 kcal/mol) > fluorene ( 3.7 kcal/mol).135 Despite all of them yielding highly delocalized hydrocarbon carbanions, the change in the size across this series has a marked effect on their solvation energies in DMSO. The effect is not limited to this solvent and a similar trend is observed for the cesium ion pairs of these carbanions in cyclohexylamine. Clearly, the larger carbanions benefit from greater charge delocalization in the gas phase, but this also reduces their solvation energy significantly and effectively destabilizes them in solution. Third, field effects caused by the interaction of an internal dipole with a carbanion are generally attenuated in solution. For example, perfluoro substitution on fluorene causes a 26.7 kcal/mol decrease in the gasphase free energy of deprotonation, but only a 16.1 kcal/mol decrease in DMSO. The internal dipoles effectively provide another mode of charge delocalization, and therefore reduce the solvation energy of the carbanion. However, there are examples where the opposite is true. A para nitro group enhances the gas-phase acidity of toluene by 28.4 kcal/mol, but the effect in DMSO is 31.2 kcal/mol. In other words, the nitro group increases the solvation energy of the resulting benzylic carbanion. This increase suggests that the solvent must have favorable electrostatic interactions with the charge-bearing oxygens of the nitro group that can overcome the effects of delocalizing the charge (Scheme 3.4).
CH |
– |
O + |
|
δ – O S δ + 3 |
|
CH2 |
|
CH3 |
|
N |
|
–O |
|
||
Scheme 3.4
4.3.4. Kinetic Acidities in the Condensed Phase. For very weak acids, it is not always possible to establish proton-transfer equilibria in solution because the carbanions are too basic to be stable in the solvent system or the rate of establishing the equilibrium is too slow. In these cases, workers have turned to kinetic methods that rely on the assumption of a Brønsted correlation22 between the rate of proton transfer and the acidity of the hydrocarbon. In other words, log k for isotope exchange is linearly related to the pK of the hydrocarbon (Eq. 13). The a value takes into account the fact that factors that stabilize a carbanion generally are only partially realized at the transition state for proton transfer (there is only partial charge development at that point) so the rate is less sensitive to structural effects than the pK. As a result, a values are expected to be between zero and one. Once the correlation in Eq. 13 is established for species of known pK, the relationship can be used with kinetic data to extrapolate to values for species of unknown pK.
log k ¼ apK þ constant |
ð13Þ |
As noted above, internal return can be a problem in kinetic acidity measurements, but Streitwieser et al.136 showed that this is not a major impediment in cyclohexyl-

BASICITY OF CARBANIONS–ACIDITY OF CARBON ACIDS |
95 |
T
Log k (relative)
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
y = |
-0.313x + 9.829 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
r 2 = 0.998 |
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
32 |
34 |
36 |
38 |
|
|
40 |
||||||||||||
pK
Figure 3.4. Plot of the rate of tritium exchange in lithium cyclohexylamide/cyclohexylamine versus cesium ion pair acidity in cyclohexylamine.137 The following species are included: (1) p-biphenyldiphenylmethane; (2) di-p-biphenylmethane; (3) triphenylmethane; (4) diphenylmethane; (5) p-methylbiphenyl.
amine. The assumption presented in Eq. 13 appears to be valid as long as structurally similar species are compared. For example, there is an excellent linear relationship between the tritium isotope exchange rates of polyaryl methanes (e.g., triphenylmethane, diphenylmethane) in lithium cyclohexylamide/cyclohexylamine solution and their cesium ion-pair pK in cyclohexylamine (Fig. 3.4).137 An a value of 0.31 is obtained for this set. When data for cyclopentadiene derivatives (e.g., indene, fluorene) are treated in a similar way, an a value of 0.37 is obtained.138 In sharp contrast are highly localized carbanions such as polyhalogenated cycloalkanes and benzenes where a values near unity are obtained.139 These results suggest that the transition state for proton transfer closely resembles the carbanion in localized systems like the benzenes and cycloalkanes, but when resonance delocalization is important in the carbanion, that stabilizing factor is not fully realized at the transition state and as a result has a lesser effect on the rate than the equilibrium acidity. This situation is easily rationalized by realizing that the transferring proton, with its significant positive charge, electrostatically localizes the charge at the site of deprotonation and limits the impact of resonance delocalization on the transition state’s stability. This finding is illustrated in Scheme 3.5 for cyclopentadiene reacting with a base, B . The positively charged proton in the transition state forces the deprotonating carbon to remain pyramidal and retain the bulk of the developing

96 CARBANIONS
negative charge, limiting the effects of resonance. In the product, the charge is fully delocalized and the effects of resonance stabilization are fully realized.
δ − δ + |
δ − |
|
‡ |
|
|
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
H |
B |
|
|
|
– |
H + H |
|
B |
|
|
|
|
|||||
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Scheme 3.5
In some cases, anomalous values have been obtained in rate–equilibrium relationships involving proton transfers. The most famous one involves nitroalkanes
where substituents cause a greater effect on the relative rate of proton transfer than the position of the equilibrium.140–144 In other words, a plot of log k versus
pK gives a slope >1. Bordwell and Hughes141 suggested an explanation much like the situation shown in Scheme 3.5. In the rate-determining step, hydrogenbonding causes charge to be localized at the carbanion center rather than on the nitro group’s oxygens. If the substituents are better able to interact with the carbanion center than the nitro group, their impact is greatest at the transition state (i.e., more charge is localized at the carbanion in the transition state). After the proton transfer is complete, the charge relocates onto the oxygens of the nitro group and the substituent’s effect is diminished. Recent computational work supports this view.145 However, it appears that nitroalkanes do not give anomalous protontransfer behavior in the gas phase so the importance of a high degree of charge delocalization onto the nitro’s oxygens seems to be a solvation phenomenon.146 As noted in Section 4.3.3, solvation has marked effects on the stability of nitrosubstituted carbanions.
In a novel kinetic approach, Dorfman et al.147 developed methods for rapidly generating very reactive carbanions such as the benzyl anion in solvent mixtures containing water and alcohols. With pulsed radiolysis techniques, they have been able to study the fast and very exothermic reactions of carbanions with these solvents. The studies have shown that despite the high exothermicity, the protonation is not diffusion controlled and depends on the nature of the carbanion’s counterion.
4.4. Carbon Acidities and Bond Strengths
A very useful thermodynamic cycle links three important physical properties: homolytic bond dissociation energies (BDE), electron affinities (EA), and acidities. It has been used in the gas phase and solution to determine, sometimes with high
accuracy, carbon acidities (Scheme 3.6).148 For example, the BDE of methane has been established as 104:9 0:1 kcal/mol149 and the EA of the methyl radical, 1:8
0:7 kcal/mol, has been determined with high accuracy by photoelectron spectroscopy (PES) on the methyl anion (i.e., electron binding energy measurements).55 Of course, the ionization potential of the hydrogen atom is well established, 313.6 kcal/ mol, and as a result, a gas-phase acidity ( Hacid) of 416:7 0:7 kcal/mol has been

REACTIVITY 97
|
|
BDE |
|
|
|
|
AH |
|
|
A |
+ |
H |
|
|
||||||
|
−EA(A ) |
|
|
|
||
A |
|
|
A– |
|
|
|
IP(H ) |
|
|
||||
H |
H + |
|
|
|||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|
|
|
AH |
∆HRXN |
A– |
+ |
H+ |
||
|
|
|||||
∆HRXN = BDE |
− |
EA(A ) + IP(H ) |
||||
Scheme 3.6
determined for methane.54 The cycle can also be used to calculate BDEs using acidity and EA data. Accurate bond strengths in fundamental species such as acetylene150 and benzene151 have been determined in this way. Finally, the same set of equations can be applied to condensed-phase data with the terms taking slightly different meanings (e.g., instead of EA, the reduction potential of the radical is used). This approach has been widely exploited by Bordwell and co-workers152 who have used their extensive set of acidity measurements in DMSO as a foundation for determining a wide range of C H BDE values. Note that earlier, Breslow153 applied a related set of equations and used electrochemical data to estimate the acidity of very weak carbon acids.
5. REACTIVITY
Carbanions play critical roles in a wide variety of reaction pathways. As stated in the Introduction, this chapter will not focus on the synthetic utility of carbanions, but will instead focus on their mechanistic significance. In this section, a sample of important reaction mechanisms that involve transient or relatively short-lived carbanion intermediates will be introduced. As you will see, the key element in these mechanisms is the ability to form a carbanion that is reasonably stable, and often the kinetics of the reactions are dominated by carbanion stability. The role of carbanion intermediates in elimination reactions will be presented in some detail as a way to illustrate some of the methods that have been developed to probe for carbanion intermediates in reaction mechanisms. Other processes including additions and rearrangement reactions will be presented in less detail, but the role of carbanion stability in these reactions will be outlined.
5.1. Carbanion Intermediates in Elimination Reactions
It is well known that base-induced elimination reactions can proceed either by
a single, concerted step (E2), or by two steps, proton transfer and leaving group expulsion, with a carbanion intermediate (E1cB) to yield an alkene.154–156 The

98 CARBANIONS
deciding factor between the two pathways is whether the carbanion intermediate is stable enough such that the leaving group expulsion step has a barrier on the potential energy surface. In simple alkyl halide systems (e.g., ethyl bromide), the carbanion is a high-energy species and the leaving group expulsion step does not have a barrier so the two steps, merge into one and an E2 mechanism is observed. However, if powerful carbanion stabilizing groups are introduced at the b-carbon, it is possible to shift the system to an E1cB pathway.
|
|
|
|
|
|
|
δ – |
|
|
|
‡ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
k E2 |
B |
|
|
|
|
|
|
||
|
|
|
|
|
H |
|
|
|
|
|
|||
|
H |
E2 |
|
|
|
|
|
|
C |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
B– + |
|
|
|
|
|
|
|
X δ – |
|
|
|
||
C C |
|
|
|
|
|
|
|
|
|
BH + C C + X – |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
E1cB |
|
|
|
|
|
|
|
|
|
|
||
|
X |
|
k1 |
|
|
|
|
|
|
||||
|
|
|
|
|
– |
|
|
k |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
BH |
+ |
C |
C |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
k-1 |
|
|
X |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Scheme 3.7
As indicated in Scheme 3.7, the first step of an E1cB mechanism can be reversible and therefore deprotonation at the b-carbon does not always lead to product formation. By applying a steady-state approximation to the carbanion concentration, the following rate law is obtained for an E1cB reaction:
rate ¼ kobs½RX&½B & kobs ¼ |
|
|
|
k2k1 |
|
|
ð14Þ |
|
k |
1 |
½ |
BH |
& þ |
k |
2 |
||
|
|
|
|
|
||||
The carbanion can be destroyed in two ways, k2 or k 1, and two limiting types of behavior are expected for E1cB mechanisms. If k2 k 1[BH], then the carbanion always decomposes to the alkene product and the rate law simplifies to kobs ¼ k1. In other words, the rate is only dependent on carbanion formation and the rate law has a form that is identical to what would be obtained in a concerted E2 reaction. This has been referred to as an E1cBIRR mechanism, where IRR indicates that deprotonation is irreversible. On the other hand, if k2 k 1[BH], then carbanion formation rarely leads to the product and the rate law simplifies to the following:
k2k1 |
ð15Þ |
kobs ¼ k 1½BH& |
These reactions often have been run in buffer solutions where [B ] and [BH] represent the concentrations of the buffer’s components. In Eq. 15, it can be seen that the rate depends on the concentration of the proton donor in the buffer solution. The

REACTIVITY 99
factor k1/k 1 also appears in the expression and is a measure of the relative acidities of the buffer acid [BH] and the elimination substrate [RX] (i.e., the more acidic the substrate, the higher k1/k 1 and kobs). The limiting behavior defined by Eq. 15 has been referred to as E1cBR, where R indicates reversible deprotonation. Establishing experimental evidence for the E1cB mechanisms has proven to be challenging because their rate laws are nearly indistinguishable under many circumstances. As noted above, the E1cBIRR mechanism shares the same rate law as an E2 mechanism. Moreover, the rate law for an E1cBR mechanism takes the same form under common experimental conditions. Often in these elimination reactions, the solvent is the conjugate acid of the base (e.g., MeO / MeOH solutions). In this case, BH becomes a constant and Eq. 15 simplifies to kobs ¼ k2k1=k 1, the same form that is expected for an E2 or an E1cBIRR mechanism (i.e., kobs is independent of any concentrations). Generally, it has taken the assembled data from a set of experiments to elucidate the mechanisms of E1cB processes.
There are a few obvious differences in the mechanisms that can be exploited in an effort to distinguish between them. First, the reversible nature of the first step in an E1cBR mechanism allows for the possibility of hydrogen/deuterium (H/D) exchange on the b-carbon in competition with elimination. Second, large primary deuterium isotope effects are expected for E2 and E1cBIRR mechanisms because Cb H cleavage is part of the rate-determining step, whereas the preequilibrium nature of an E1cBR mechanism should lead to a much smaller deuterium isotope effect. Third, isotope or substituent effects associated with the leaving group should be most evident in E2 or E1cBR mechanisms because leaving group cleavage is part of the rate-determining step. Finally, the concentration of the conjugate acid of the base only appears in the rate law of an E1cBR mechanism. The work of Keeffe and Jencks157,158 on the eliminations of p-nitrophenylethylammonium ions provides a good illustration of the strategies needed to solve this complex mechanistic problem. In this case, isotope exchange offers one clue to the mechanistic pathway. If an E1cBR mechanism is active, then isotope exchange at the b-carbon should be possible because in this mechanism, the b-carbon should be deprotonated/reprotonated multiple times before the elimination occurs (i.e., the first step is fast relative to the second one in the E1cBR mechanism). For example, when the substrate in Scheme 3.8 was treated with a basic buffer in D2O, the 1H NMR spectrum indicates that the b-hydrogens in the substrate are almost completely replaced by deuterium by the time that the elimination reaction has reached 50% completion.
|
|
|
|
|
+ |
|
|
|
O2N |
CD2 CH2 |
N |
|
+ |
B– |
+ |
|
|
O2N |
CH2 CH2 N |
|
|
|
|
D2O |
|
||||
|
|
|
|
||
After 50% conversion to alkene |
|
O2N |
CH CH2 + O2N |
CD CH2 |
|
|
|
|
|
||
Scheme 3.8

100 CARBANIONS
It has been argued that the occurrence of isotope exchange at the b-carbon does not prove an E1cBR mechanism, only that a carbanion is formed under the reaction
conditions—it is possible that an E2 process is responsible for product formation (i.e., k1 > kE2 > k2k1/k 1[BH]).159 In other words, the carbanion is formed and
exchanges quickly, but the elimination from the carbanion intermediate (k2) is
slow relative to a concerted E2 reaction. To further probe the mechanism, Keeffe and Jencks157,158 examined the effect of buffer concentration and solvent
isotope (H2O vs. D2O) on the rate. In their system, they found that increasing [B ] while keeping [B ]/[BH] constant led to a curved plot of rate versus [B ]. This result is consistent with Eq. 14 (i.e., kobs is dependent on [BH] and changes with increasing buffer concentration) and suggests a situation where k 1[BH] must at least be of comparable magnitude to k2 (i.e., not an E1cBIRR mechanism). Here, increasing [B ] and [BH] causes the rate of deprotonation and reprotonation to increase, shifting the system toward the E1cBR extreme (Eq. 15). They also found a large, inverse solvent isotope effect, which again is consistent with Eq. 14. In D2O, k 1 is diminished by a primary isotope effect, and therefore the carbanion intermediate has a longer lifetime and a greater propensity for forming the alkene product. Taken together, the data clearly point to an E1cB mechanism where k2 is either partly or entirely rate determining (i.e., E1cBR).
Identifying E1cBIRR reactions presents special problems because the rate law takes the same form as an E2 reaction and, like an E2 reaction, it should display a large primary kinetic isotope effect when the b hydrogens are substituted with deuterium. Distinguishing between them requires evidence concerning the cleavage of the C X bond in the rate-determining step. For an E2 reaction, there should be extensive cleavage of this bond, but in an E1cBIRR reaction, it is only moderately weakened by a hyperconjugative interaction of the carbanion lone pair with the C X bond. Curvature in linear free-energy relationships based on substituents attached to the leaving group has been used as evidence for the emergence of an E1cBIRR mechanism. Because the leaving group will bear a smaller negative charge in an E1cBIRR than an E2 mechanism, it should be less susceptible to the effects of electron-donating or -withdrawing groups. In the case of fluorenylmethyl benzenesulfonates (11) reacting with amine bases,160 distinct curvature and a shift to a shallower slope (i.e., substituent has smaller effect on rate) is observed in a Hammett-type107 substituent effect plot when electron-donating groups are added to the benzenesulfonate. Of course, these groups make the benzenesulfonate a weaker leaving group (i.e., stronger base) and apparently provide marginal stability to the carbanion intermediate and shift the mechanism from E2 to E1cBIRR.
O
αO S
H |
β O |
Z |
β |
|
|
H
α X
11 |
12 |
