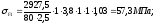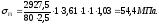1-3 / курксовая / Моё / 4 РАСЧЕТ ЗАКРЫТОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ(ГОСТ)

4 РАСЧЕТ ЗАКРЫТОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ

Исходные данные:

n₁=424 мин^-1 ; ω₁=44,4 рад/с Т₁=117,1 ; Р₁=5,2 КВт;

n₂=106 мин^-1 ; ω₂=11,1 рад/с Т₂=441,4 ; Р₂=4,9 КВт;

U=4 t_р=12500 ч

4.1 Выбор механических характеристик материалов передачи и определение допускаемых напряжений:

4.1.1 Выбор материала, термообработки и твёрдости.

Шестерня: сталь 45 (ГОСТ 1050 – 88);

Обработка улучшением, твёрдость заготовки 248НВ₁.

Зубчатое колесо: сталь 45 (ГОСТ 1050 – 88);

Обработка нормализация, твёрдость заготовки 193НВ₂.

4.1.2 Число циклов нагружения зубьев:

для зубьев шестерни: N₁=60·n₁·t_p;

N₁=60·424·12500=318·10⁶.

для зубьев колеса: N₁=60·n₂·t_p;

N₁=60·106·12500=795·10⁵.

4.1.3 Определение допустимых контактных напряжений:

Допустимые напряжения при расчёте на усталостную контактную прочность:

для шестерни

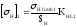
для колеса ,

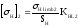где - предел выносливости зубьев при контактном нагружении:

для шестерни

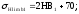
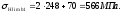
для колеса

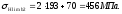
S_H-коэффициент безопасности, S_H=1,1;

K_HL-коэффициент долговечности;

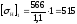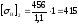МПа;

МПа.

В качестве допускаемого контактного напряжения принимаем

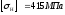
4.1.4 Определение допустимых изгибных напряжений:

для шестерни ;

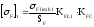для колеса ;

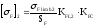где -предел выносливости зубьев при изгибном нагружении

для шестерни

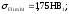
для колеса

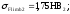
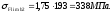
S_F-коэффициент безопасности (S_F=1,1);

K_FС-коэффициент реверсивности(K_FC=1 для нереверсивной передачи).

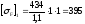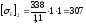МПа;

МПа.

4.2 Определение межосевого расстояния:

,

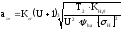где K_α-коэффициент, для прямозубых передач K_α=495;

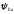-коэффициент ширины зубчатого венца. При симметричном расположении 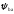=0,4.

K_Hβ- коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба. Для прирабатывающихся зубчатых колёс K_Hβ=1.

мм.

Округлим до стандартного значения: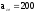мм

4.3 Определение модуля зубьев:

m_n= (0,01…0,02) · а_ω=0,015·200=3, возьмем стандартное значение m_n=2,5

4.4 Суммарное число зубьев шестерни и колеса:

z_∑ = ;

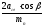где β – угол наклона зубьев, у прямозубых колес β =0º

z_∑ = .

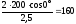4.5 Число зубьев шестерни:

z₁ =.

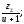z₁ =.

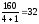4.6 Число зубьев колеса:

z₂ = z_∑ - z₁;

z₂ =160-32=128.

4.7 Фактическое передаточное число:

U_ф =

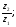
U_ф =

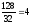
4.8 Диаметр делительной окружности:

шестерни d₁ =

d₁ =

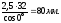
колеса d₂ =

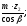
d₂ =

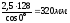
4.9 Диаметр окружности вершин зубьев:

шестерни d_a1 = d₁ + 2·m;

d_a1 =80+2·2,5=85мм.

колеса d_a2 = d₂ + 2·m;

d_a2=320+2·2,5=325мм.

4.10 Диаметр окружности впадин зубьев:

шестерни d_f1 = d₁ – 2,5 · m;

d_f1 =80-2,5·2,5=74мм.

колеса d_f2 = d₂ – 2,5 · m;

d_f2 =320-2,5·2,5=314мм.

4.11 Ширина зубчатых венцов:

колеса b₂ = ψ_ba · a_ω;

b₂ =0,4·200=80мм.

шестерни b₁ = b₂ + 3;

b₁ =80+3=83мм.

4.12 Окружная скорость зубчатых колес:

υ = ω₁ ·

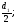
υ

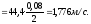
степень точности = 9.

4.13 Силы в зацеплении:

Окружные F_t1 = F_t2 =

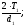
F_t1 = F_t2 =

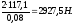
Радиальные F_r1 = F_r2 =

F_r1 = F_r2 =

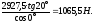
Схема действия сил представлена на рисунке 4.1.

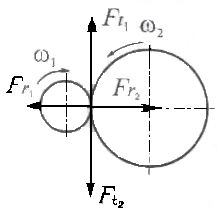
Рис. 4.1 – Схема действия сил

4.14 Контактное напряжение:

σ_н = К’_a

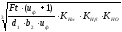
К’_a - коэффициент, К’_a = 436; _Нα – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями,К_Нα = 1,0; К_Нβ– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба, К_Нβ = 1; К_НО – коэффициент динамической нагрузки, К_НО = 1,1.

σ_Н = 436 ·

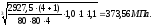
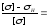
Проверка: 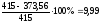% - недогруз.

4.15 Напряжение изгиба:

для зубьев шестерни σ_F1 =

для зубьев колеса σ_F2 = ,

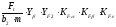Y_β- коэффициент, учитывающий наклон зубьев, Y_β=1; Y_F – коэффициент формы зуба, Y_F1=3,8, Y_F2=3,61; К_Fα– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, К_Fα=1; К_Fβ– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба, К_Fβ=1; К_Fυ– коэффициент динамической нагрузки, К_Fυ=1,03.

25