Раздел 1. Цепи постоянного тока.

Задача 1.1

Определить

Ответ:

Задача 1.2

Определить

Ответ:

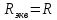
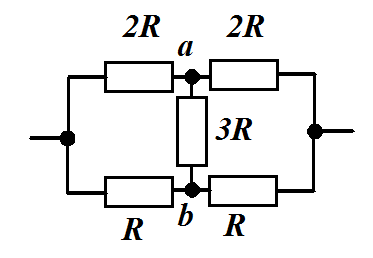
Задача 1.3

Определить

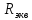
1) Потенциалы узлов а и b равны. Сл. это

Ответ: Проверить преобразованием треугольника в звезду

Задача 1.4

Определить

Ответ:

Задача 1.5

До коммутации ток в цепи 1А. Определить ток после коммутации ключа.

Ответ: 1.5А

Задача 1.6

До коммутации ток в цепи 1А. Определить ток после коммутации ключа.

Ответ: 3А

Задача 1.7

Определить схемы в случае подключения ее к зажимамab и ac. Сопротивление ветви каждого из участков равно R.

Ответ:

Задача 1.8

Определить (R_АВ ) схемы

Ответ:

Задача 1.9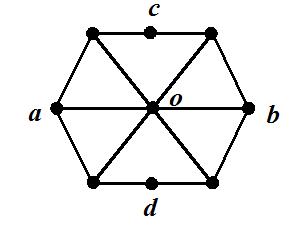

Определить 1) 2)Сопротивление каждой ветвиR

Ответ: ,

Решение:

1) В силу симметрии ток в узле o отсутствует, т.е. эта точка есть точка равного потенциала

2) Потенциал точек а и b одинаков. Схему можно представить как

Сопротивление ромба R. Сопротивление половины цепи вдоль cd 2R, следовательно

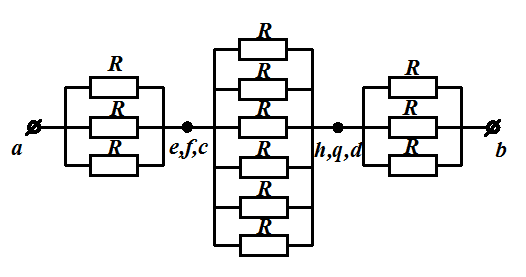
Задача 1.10

Сопротивление ребра куба R.

Определить 1) R_АВ ; 2) R_АС ; 3) R_AD

Решение:

1. Потенциалы точек c, f, e одинаковы – это одна точка, а точки h, q, d – другая точка

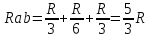
2. Точки одинакового потенциала c и f, точки q и d

4. 

3) Точки f и c и точки n и q имеют равные потенциалы. Эквивалентная схема.

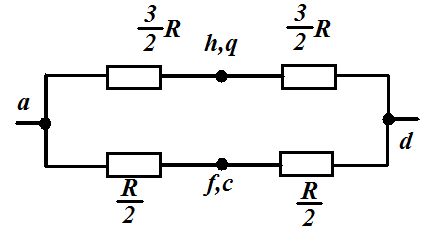
Узлы n, q и f, c имеют одинаковый потенциал сопротивление R/2 между ними можно не учитывать, так как ток через него не идет.

Ответ: 1) 2)3)

Задача 1.11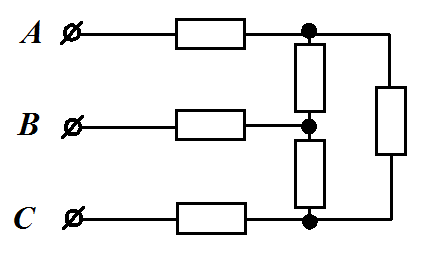

Решение: В левой схеме одинаковое сопротивление по 3 Ома. Определяем радиус правой схемы, чтобы они были эквивалентными.

В левой схеме преобразуем треугольник в звезду

В правой схеме преобразуем внешний треугольник в звезду.

Точки О и О’ имеют одинаковый потенциал и могут быть соединены.

Отсюда общее сопротивление

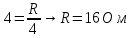
Задача 1.12

E=17 В

R₁=R₂=R₃=R₄=3 Ом

R₅=5 Ом

Решение:

Преобразуем треугольник(1,2,3) в звезду(1,2,3)

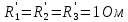
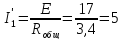
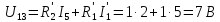
В исходной схеме:

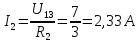
Баланс мощностей:

Задача 1.13. Определить .

Ом

Ом

Ом

Ом

Ом

Ом

Ответ: Ом

Задача 1.14. Определить токи в ветвях.

В

В

А

Ом

Ом

Ом

Решение:

На основании законов Кирхгофа:

В схеме 5 ветвей (b = 5) и 3 узла (y = 3)

По уравнений

(1 узел)

(2 узел)

По 2 закону Кирхгофа

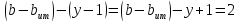
Обход контуров по часовой стрелке.

(1 контур)

(2 контур)

Ответ: А

А

Задача 1.15. Определить токи в ветвях.

В

В

А

Ом

Ом

Ом

Решение:

Применяем метод контурных токов.

Независимых контуров два . Добавлен третий контур с источником тока У, его контурный токА

Уравнение цепи:

где

;

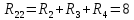отсюда токи: 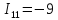А

А

Произвольно выберем направление токов ветвей и найдем их.

А

А

А

А

Ответ: А

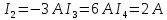
Задача 1.16. Определить токи по М.У.Н.

В

В

А

Ом

Ом

Ом

Решение:

Примем за опорный узел 3.

Составим уравнение по М.У.Н.

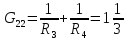
откуда

В

Уравнение баланса мощности:

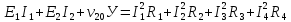
408 Вт = 408 Вт

Ответ: А

Задача 1.17. Решить задачу №14 методом наложения

С помощью закона Ома рассчитываем токи в цепи от действия каждого источника

Токи от действия источника :

Токи от действия источника :

Токи от действия источника тока J

Токи исходной цепи:

Задача 1.18. Схема задачи №1.14.

Определить ток первой ветви методом эквивалентного генератора

Решение: Разрешаем цепь относительно первой ветви

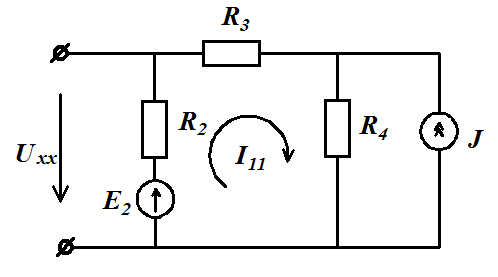
Для определения определяем токметодом контурных токов из уравнения

,откуда и

Задача 1.19

Определить токи ветвей

Ответ:

Баланс мощностей:

Источник работает в режиме генератора, источник– потребляет энергию

Задача 1.20.

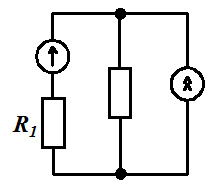
Определить токи

Ответ:

Задача 1.21.

Определить токи методом контурных токов

Ответ:

Задача 1.22

Определить токи методом контурных токов

Ответ:

Задача 1.23.

Определить токи и

1. Методом двух узлов

2. Методом наложения

Ответ:

Задача 1.24.

Определить токи методом узловых напряжений

Ответ: