Informatika_met_ukazania

ББК 73я73

И 741

Составитель Н.Э. Унру, канд. техн. наук, доц.

Рецензенты:

И.С. Грузман, д-р техн. наук, проф., С.П. Новицкий, д-р техн. наук, проф., В.П. Разинкин, д-р техн. наук, проф., В.Р. Снурницин, канд. техн. наук, доц., С.В. Тырыкин, канд. техн. наук, доц.

Работа подготовлена на кафедре радиоприемных и радиопередающих устройств

© Hовосибиpский государственный технический университет, 2009

2

3

ПРЕДИСЛОВИЕ

Среди широко распространенных математических систем (MathCAD, Maple, Mathematica и др.) рассматриваемая в настоящих методических указаниях система MatLab (Matrix Laboratory) является не только самой обширной и мощной, но имеет и самую простую адаптацию к решению задач пользователя. В основу этой системы положена идея создания языка программирования для решения сложных научно-технических задач на базе представления данных в форме матриц с возможностью доступа пользователя к ее исходным кодам и возможностью ее практически неограниченного расширения [1].

Каждая лабораторная работа содержит помимо цели, пояснений, порядка выполнения работы также контрольные вопросы и задания. Перед работой над вариантом задания студенту рекомендуется ознакомиться с содержанием пояснений и выполнить имеющиеся там примеры. После предъявления преподавателю выполненного варианта задания лабораторная работа должна быть защищена.

Отчеты по лабораторным работам представляются по указанию преподавателя в твердой или электронной форме и должны помимо титульного листа с вариантом задания содержать: цель работы, тексты заданий, разработанные коды в виде М-файлов, графики и выводы.

4

Лабораторная работа № 1

ПЕРВОЕ ЗНАКОМСТВО С МАТЕМАТИЧЕСКОЙ СИСТЕМОЙ MATLAB

Цель работы – ознакомление с программной системой для математических расчетов MatLab R2007b и получение первоначальных навыков ее использования.

MatLab – это мощное и универсальное программное средство решения задач, возникающих в различных областях человеческой деятельности. Его можно использовать при матричном анализе, обработке сигналов и изображений, решении задач математической физики и оптимизационных задач, обработке и визуализации данных, работе с картографическими изображениями и многом другом.

Пользовательский интерфейс

Запуск MatLab R2007b производится стандартным для Windows способом. Типичный вид экрана монитора при работе с MatLab R2007b показан на рис. 1. Для установки вида окна, принятого по умолчанию, следует левой кнопкой мыши (ЛКМ) выбрать меню Desktop Desktop Layout Default.

Ограничимся рассмотрением только тех пунктов меню, которые не являются стандартными для Windows и представляют наибольший интерес при выполнении (в рамках настоящих методических указаний) математического моделирования радиотехнических цепей и процессов

Workspace As… позволяет сохранить значения всех переменных и настройки текущей рабочей среды в файле с расширением mat. Это рекомендуется делать после завершения очередного этапа работы над проектом.

Пункты Clear Command Window, Clear Command History и Clear Workspace в меню Edit позволяют очистить соответственно командное окно, окно истории команд и окно переменных. Очистку указанных окон рекомендуется выполнять перед началом работы над новым проектом, например над новой лабораторной работой.

В меню Desktop имеется большой набор возможностей для придания рабочему столу удобного для работы вида.

5

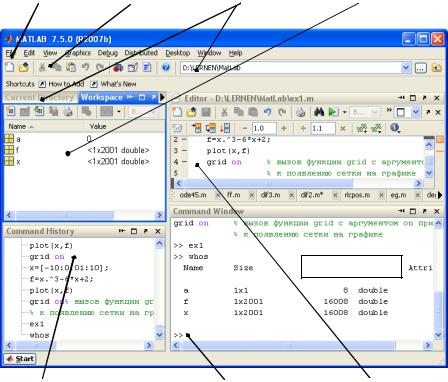
Окно переменных (Workspace) позволяет быстро и просто получить информацию не только о доступных переменных, но и проконтролировать их значения (двойным щелчком ЛКМ).

Окно текущего каталога (Current Directory) содержит информа-

цию о всех файлах, находящихся в текущем каталоге. Любой М-файл (в колонке Type у такого файла стоит запись M-file) двойным щелчком ЛКМ может быть загружен в редактор М-файлов (Editor). Перед началом выполнения нового проекта для хранения всех относящихся к нему материалов рекомендуется создать новую рабочую папку (например, C:\temp\Laba1), а во время работы с проектом делать эту папку текущей.

Командное окно

Рис.1. Рабочее окно MatLab R2007b

6

Окно История команд удобно тем, что позволяет быстро найти, вызвать, скопировать или удалить ранее уже набранную команду. Для удаления команды ее следует выделить ЛКМ и стандартным для Windows способом (клавиша <Delete>) удалить.

В Командном окне содержатся перечень последних поданных команд, результаты их выполнения и служебные сообщения.

Каждое из перечисленных выше четырѐх окон может быть легко

(щелчком ЛКМ по иконке (Undock − вывести из дока)) сделано самостоятельным окном; обратная процедура выполняется аналогично

щелчком ЛКМ по иконке (Dock − поставить в док).

Некоторые из основных приемов работы в MatLab

В MatLab используются все буквы латинского алфавита и арабские цифры от 0 до 9. В MatLab, как и в С++, большие и малые буквы различаются. Кроме букв латинского алфавита используются все специальные символы клавиатуры компьютера. Все символы после символа «%» до конца текущей строки рассматриваются как комментарии.

Выполнение арифметических вычислений. Используются сим-

волы: «+», «–», «*», «/» и «^» (возведение в степень). Для установления приоритета выполнения действий следует использовать круглые скобки «()», а для подавления печати результата вычислений необходимо применять символ «;». Пусть необходимо вычислить следующее вы-

23.2

ражение: 4.7 4 5.6 .

Щелкнем ЛКМ в командной строке (там после этого должен появиться мигающий курсор), наберем последовательность символов 2^3.2/4.7-4*5.6 и нажмем на клавишу <Enter>. В рабочем окне появится запись

>> 2^3.2/4.7-4*5.6 ans =

-20.4448

>>

В конце будет расположен мигающий курсор.

7

Если набрать последовательность символов 2^3.2/4.7-4*5.6; и тоже нажать на клавишу <Enter>, то в рабочем окне появится другая запись:

>> 2^3.2/4.7-4*5.6;

>>

с мигающим курсором в конце. Печать результата вычислений здесь подавлена символом «;». Результат хранится в переменной с именем ans, и для его получения следует в командной строке набрать ans<Enter>. Кроме того, в дальнейших вычислениях имя этой переменной (ans) можно подставлять вместо результата вычислений.

Если имеется необходимость повторно в командном окне вызвать ранее введенную запись, то это легче всего сделать, используя клави-

ши < > и < >.

Вообще говоря, имя переменной может состоять из букв латинского алфавита, знака подчеркивания и цифр, и оно обязательно должно начинаться с буквы. Для того чтобы проверить, занято ли уже какоелибо имя, следует набрать в командной строке exist(‘имя переменной’). Нулевой ответ при выполнении этой команды (вызова функции exist) говорит, что имя свободно.

Пример: >> exist('a6') ans =

0

Для изменения формата выводимых числовых данных можно поступить двумя способами. Первый состоит в вызове в командной стро-

ке функции format с одним из ее аргументов: short, short e, long, long e, short g, short eng, long g, long eng, bank, compact, loose.

Пример:

>> format short

Второй способ состоит в вызове (ЛКМ через меню File Preferences…) окна Preferences, которое представлено на рис. 2. Здесь в ниспадающем списке элемента Numeric format: и следует выбрать желаемый числовой формат для выводимых данных. Помимо этого там же ниже в элементе Numeric display: можно изменить и вид выводимой в командном окне информации (компактный − compact или свободный − loose). Завершить выбор следует щелчком ЛКМ по кнопке <OK>.

8

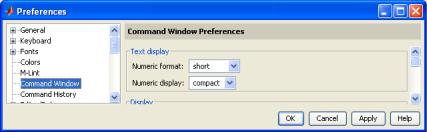
Рис. 2. Окно Preferences

Массивы и работа с ними. Все данные MatLab представляет в виде массивов. Простое число представляется в виде двумерного массива размером один на один. Массив − это упорядоченная, пронумерованная совокупность однородных данных, имеющая имя. Массивы бывают одномерными (вектор-столбцы и вектор-строки), двумерными и многомерными. В MatLab нумерация элементов массивов начинается с единицы.

Ввод вектор-строки осуществляется в квадратных скобках. Элементы следует отделять друг от друга пробелом или запятой.

Пример:

>> a=[0.8 2.3 9.1] a =

8.0000e-001 2.3000e+000 9.1000e+000

Примечание. Если в результате описанных выше действий на экране появилась запись тех же чисел, но в другом виде, например

a =

0.8000 2.3000 9.1000,

то это означает, что в MatLab установлен другой формат выводимых числовых данных и его при желании можно изменить, как было показано выше.

Ввод вектор-столбца также осуществляется в квадратных скобках, но при этом элементы отделяются друг от друга точкой с запятой.

Пример:

>> b=[-2.2;5.9;0.7] b =

-2.2000e+000 5.9000e+000 7.0000e-001

9

Над векторами определены следующие операции: вычисление длины, транспонирование, сложение, вычитание, умножение на число, скалярное и векторное (только для трехэлементных векторов) произведение, как показано ниже:

y=

-4.3000 1.1000 0.1000

Векторы могут быть элементами при определении новых векторов, например:

>> ac=[a,c] ac =

0.8000 2.3000 9.1000 0.2000 0.7000 0.9000 >> act=[ar;c']

act = 0.8000 2.3000 9.1000

10