Лекции_тервер

аддитивность вероятности (аксиома P3), а затем теорему умножения 6.3,

Теорема 7.3 (формулы Байеса12). Пусть H1, H2, . . . – полная группа событий и A — некоторое событие положительной вероятности. Тогда условная вероятность события Hk при условии, что событие A произошло, для любого k вычисляется по формуле

P(Hk)P(A|Hk) P(Hk|A) = ∑∞ .

P(Hi) P(A|Hi)

i=1

Доказательство. По определению условной вероятности имеем

где последнее равенство следует из теоремы умножения и формулы полной вероятности.

§8. Повторные испытания

Рассмотрим испытание (опыт) M, имеющий конечное пространство, состоящее из m элементарных исходов, заданное рядом распределения

см. опред. 4.5. Примеры таких опытов нам встречались: подбрасывание ломаного гроша, см. прим. 4.6.2); подбрасывание игральной кости или двух костей; подбрасывание выпуклого многогранника, см. прим. 4.6.3). Многие математические модели случайных явлений связаны с опытом, который называется схемой повторных испытаний.

Определение 8.1. Схема повторных испытаний — это новый опыт N, состоящий в последовательном проведении n раз одного и того же испытания M или, что одно и то же, одновременное проведение n одинаковых испытаний M.

12Томас Байес (Reverend Thomas Bayes, 1702 — 1761), английский математик и пресветерианский священник.

31

Случай Бернулли m = 2.

При m = 2 испытание M можно интерпретировать как подбрасывание ломаного гроша, а опыт N состоит в подбрасывании ломаного гроша n раз.

Задача о ломаном гроше. Какова вероятность, обозначим её через Pn(k), того что в результате n подбрасываний орёл выпадет k раз (0 ≤ k ≤ n)?

Заметим, что остальные n−k раз выпадет решка. Ясно, что опыт N имеет конечное пространство элементарных событий Ω = {0, 1, 2, . . . , n}, потому что орёл может либо не выпасть ни разу, или выпасть 1 раз, или 2 раза, ... , или n раз. На этот вопрос отвечает следующая теорема.

Теорема 8.2. Для любого k Ω имеет место формула Бернулли

Pn(k) = Cnkpk(1 − p)n−k = Cnkpkqn−k.

Доказательство. Рассмотрим один из благоприятных элементарных исхо-

дов: o, o, ..., o, p, p, ..., p. Через o и p обозначены соответственно появления

| {z } | {z }

k раз n−k раз

орла и решки. Поскольку испытания независимы, то по опред. 5.1 вероятность элементарного исхода, состоящего в том, что первые k раз выпал орёл, и в остальные n − k раз выпадет решка, равна pk(1 − p)n−k.

Другие элементарные исходы, благоприятствующие выпадению k орлов, отличаются от рассмотренного исхода o, o, ..., o, p, p, ..., p лишь перераспре-

называется биномиальным распределением.

Название этого распределения связано с тем, что сумма вероятностей из второй строки ряда распределения может быть вычислены по формуле бинома Ньютона, т.е.

32

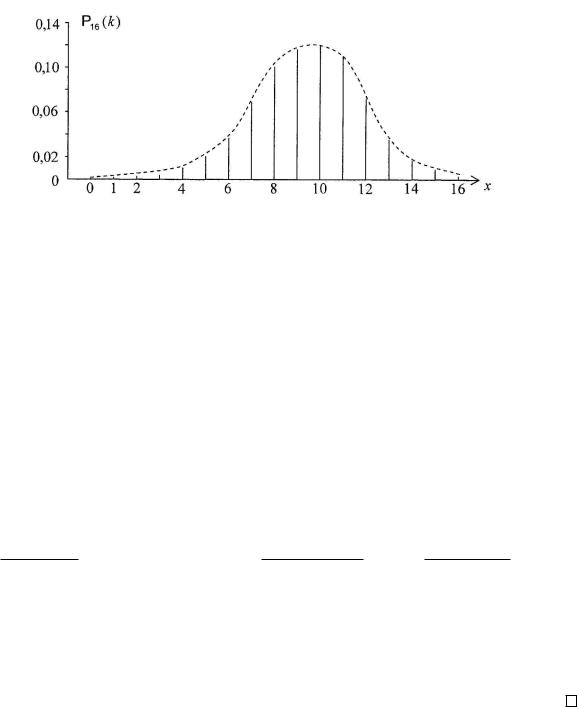
Рис. 12: График биномиального распределения при n = 16.

Возникает естественный вопрос. Какое число успехов при n испытаниях наиболее вероятно? Другими словами, при каком k достигается максимум функции Pn(k) = Cnkpkqn−k?

Теорема 8.4. Если в схеме Бернулли вероятность появления орла равна p, то в биномиальном распределении с n испытаниями наиболее вероятным числом орлов является либо

а) единственное число [np + p], если число np + p не целое, здесь [x] означает целую часть числа x, либо

б) два числа np + p и np + p + 1, если число np + p целое.

1.Pn(k) > Pn(k − 1) при np + p − k > 0, т.е. при k < np + p;

2.Pn(k) < Pn(k − 1) при np + p − k < 0, т.е. при k > np + p;

3.Pn(k) = Pn(k − 1) при np + p − k = 0, что возможно, лишь если np + p

— целое число.

Общий случай m ≥ 3.

При m ≥ 2 испытание M можно интерпретировать как подбрасывание выпуклого многогранника, имеющего m граней, см. прим. 4.6.3). Такое испытание имеет ряд распределения

33

где p1 + p2 + . . . + pn = 1. Опыт N состоит в подбрасывании многогранника n раз (n повторных испытаний).

Задача о многограннике. Какова вероятность, обозначим её через Pn(m1, m2, . . . , mk), того что в результате n подбрасываний

Ясно, что опыт N имеет пространство элементарных событий Ω, которое имеет конечное число элементарных событий равное числу неотрицательных решений уравнения ( ).

Пример 8.5. Асимметричный тетраэдр, грани которого обозначены ω1, ω2, ω3, ω4 подбрасывают 14 раз. Вероятности выпадения тетраэдра на эти

где m1, m2, . . . , mk ≥ 0. Эта формула мы докажем как след. 8.10; по аналогии c (bN) будем назвать её полиномом Ньютона.

Лемма 8.7 (о сумме полиномиальных коэффициентов). Сумма полиномиальных коэффициентов равна kn, т.е.

34

Доказательство. Подставим в полином Ньютона p1 = p2 = · · · = pk = 1, получим требуемый результат.

Лемма 8.8 (о сумме полиномиальных вероятностей). Если p1 + p2 + · · ·+ pk = 1, то сумма членов в правой части полинома Ньютона равна единице,

Доказательство. Подставим в полином Ньютона p1 + p2 + · · · + pk = 1, получим требуемый результат.

Теорема 8.9 (о повторных подбрасываниях многогранника). Для опыта, состоящего из n подбрасываний многогранника имеет место формула

Доказательство. Рассмотрим один элементарный результат n кратного подбрасывания многогранника:

Это один из благоприятных исходов: сначала событие ω1 произошло m1 раз, затем событие ω2 произошло m2 раз, ..., и, наконец, событие ωk произошло mk раз. Вероятность этого элементарного исхода равна pm1 1 pm2 2 . . . pmk k .

Все остальные благоприятные исходы отличаются лишь расположением событий из того же набора событий на n местах. Число таких исходов равно числу способов расставить на n местах m1 событий ω1, потом m2 событий ω2,

..., и, наконец, mk событий ωk. По теор. 1.3 и 1.6 это число равно

Cnm1 · Cnm−2m1 · Cnm−3m1−m2 · ... · Cnm−km1−m2−···−mk 1 =

Теперь ясно, откуда взялся ответ в прим. 8.5.

Следствие 8.10. Справедлива формула полинома Ньютона (pN), см. стр. 34.

35

Глава 2. ТЕОРИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

§9. Случайные величины

Пусть (Ω, A, P) — произвольное вероятностное пространство. Определение 9.1. Функция ξ : Ω → R называется случайной величи-

ной на σ-алгебре событий A, если для любого числа x R прообраз луча ξ−1((−∞, x]) = {ω Ω ξ(ω) ≤ x} является событием из σ-алгебры A.

Замечание 9.2. 1) Самая простая функция ξ : Ω → R — это постоянная функция, заданная для любого ω Ω по формуле ξ(ω) = c. Она принимает одно значение и является не случайной, а детерминированной. Она рассмат-

ξ−1((−∞, x]) = {ω Ω ξ(ω) ≤ x} обозначают короче: {ξ ≤ x}.

3) Оказывается, что другие случайные величины (ξ(ω) ≠ ω) могут быть описаны через случайную величину ξ(ω) = ω. Это будет показано в § 12.

Определение 9.3. Функцией распределения случайной величины ξ называется функция Fξ : R → [0, 1], определённая по формуле

Fξ(x) = P(ξ ≤ x).

Очевидно, что 0 ≤ Fξ(x) ≤ 1.

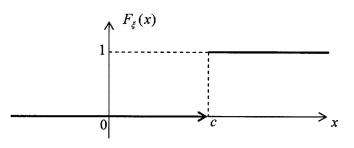
Рис. 13: Функция распределения детерминированной величины.

Примеры 9.3.1. 1) Детерминированная (вырожденная случайная) величина ξ : Ω → R имеет пространство элементарных событий, состоящее из одного элементарного события, Ω = {ω}. Она принимает только одно значение ξ(ω) = c = const R с вероятностью равной 1, т.е. имеет ряд распределения

ющая значения 1 (успех) и 0 (неудача) с вероятностями соответственно p и

36

Рис. 14: Функция распределения Бернулли.

3) Случайная величина ξ — номер грани при подбрасывании игральной кости имеет функцию распределения, показанную на рис. 15.

Рис. 15: Функция распределения выпадения числа на игральной кости.

4) Случайная величина ξ — номер появления успеха в геометрическом рас-

функцию распределения, показанную на рис. 16.

В дальнейшем мы будем использовать следующие обозначения для пределов функций слева и справа соответственно:

где всегда ε > 0.

Функция распределения Fξ(x) обладает следующими свойствами.

Теорема 9.4. 1) Fξ(x) — неубывающая функция, другими словами, если x1 < x2, то Fξ(x1) ≤ Fξ(x2).

37

Рис. 16: Функция геометрического распределения при p = 12 .

3) Fξ(x) непрерывна справа: для любой точки x0 R имеем Fξ(x0 + 0) =

Fξ(x0).

Теорема 9.5. (О связи вероятности событий-интервалов с функцией распределения.) Для любых точек x, a, b R, где a < b, имеем

1)P(ξ < x) = Fξ(x − 0),

2)P(ξ = x) = Fξ(x) − Fξ(x − 0),

3)если Fξ непрерывна в точке x, то P(ξ = x) = 0,

4)P(a < ξ ≤ b) = Fξ(b) − Fξ(a),

5)P(a ≤ ξ ≤ b) = Fξ(b) − Fξ(a − 0),

6)P(a < ξ < b) = Fξ(b − 0) − Fξ(a),

7)P(a ≤ ξ < b) = Fξ(b − 0) − Fξ(a − 0).

2) P(ξ = x) = P({ξ ≤ x} r {ξ < x}) = P(ξ ≤ x) − P(ξ < x) = Fξ(x) − Fξ(x − 0).

3) P(ξ = x) = Fξ(x)−Fξ(x−0) = Fξ(x)−lim Fξ(x−ε) = Fξ(x)−Fξ(x) = 0.

ε→0

4) P(a < ξ ≤ b) = P ({ξ ≤ b} r {ξ ≤ a}) = P(ξ ≤ b) − P(ξ ≤ a) = Fξ(b) − Fξ(a).

5) — 7) доказать самостоятельно.

38

Следствие 9.6. Если функция распределения Fξ(x) непрерывна, то

P(a ≤ ξ < b) = P(a < ξ < b) = P(a ≤ ξ ≤ b) = P(a < ξ ≤ b) = Fξ(b) − Fξ(a).

§10. Абсолютно непрерывные случайные величины

Определение 10.1. Случайная величина ξ называется абсолютно непрерывной, если существует такая неотрицательная функция fξ(x) (возможно обобщённая, см. §11), что для любого x R функция распределения Fξ(x)

представима в виде 13

∫x

Fξ(x) = fξ(t)dt.

−∞

При этом функция fξ(x) называется плотностью вероятности случайной величины ξ

Замечание 10.2. Если Fξ(x) — дифференцируемая функция распределения, то название «плотность вероятности» имеет следующее объяснение. С одной стороны, используя формулу дифференцирования интеграла по верхнему пределу, имеем = fξ(t)|t=x = fξ(x). С другой стороны, по определению производной имеем:

Поэтому

fξ(x) = P(x < ξ ≤ x + dx) dx

есть отношение вероятности попадания случайной величины ξ в интервал (x, x + dx] к длине этого интервала dx, что физически означает плотность вероятности («массы») случайной величины ξ в точке x.

Теорема 10.3. Плотность обладает свойствами:

1) fξ(x) ≥ 0 для любого x;

∞∫

2)fξ(t)dt = 1.

−∞

13В дальнейшем мы рассматриваем только такие случайные величины, для которых все связанные с ними несобственные интегралы и суммы бесконечных рядов сходятся абсолютно.

39

Доказательство. 1) По теор. 9.4.1) функция распределения Fξ(x) — неубы-

Определение 10.4. Пусть область U Rn имеет меру µ(U). Говорят, что в области U функция h : U → R удовлетворяет некоторому свойству P почти всюду, если подмножество A U, в котором свойство P не выполняется, имеет меру 0, т.е. µ(A) = 0.

Докажем свойства абсолютно непрерывных случайных величин.

Теорема 10.5. Если случайная величина ξ абсолютно непрерывна, то

1)её функция распределения Fξ(x) непрерывна в R и дифференцируема почти всюду в R, т.е. равенство fξ(x) = dxd Fξ(x) справедливо почти всюду,

2)P(ξ = x) = 0 для любого x R,

Во-вторых, функция Fξ(x) имеет не более чем счётное множество скачков, поэтому она не дифференцируема не более чем в счётном множестве точек. Любое счётное множество точек на прямой имеет нулевую меру (длину). По-

Остальные равенства следуют из 9.6.

Примеры абсолютно непрерывных случайных величин

Определение 10.6. Случайная величина ξ имеет равномерное распреде-

Графики функций Fξ(x) и fξ(x) показаны на рис. 17. Заметим, что в точках a и b функция распределения Fξ(x) не дифференцируема, поэтому

40