
alekseev дискретная математика 2012
.pdfНижегородский государственный университет им. Н.И. Лобачевского
Национальный исследовательский университет
Учебно-научный и инновационный комплекс
"Модели, методы и программные средства"
Основная образовательная программа
010300 «Фундаментальная информатика и информационные технологии», общий профиль, квалификация (степень) бакалавр
Учебно-методический комплекс по дисциплине
«Дискретная математика»
Основная образовательная программа
010400 «Прикладная математика и информатика», общий профиль, квалификация (степень) бакалавр
Учебно-методический комплекс по дисциплине
«Дискретная математика»
В.Е. Алексеев, Л.Г. Киселева, Т.Г. Смирнова
СБОРНИК ЗАДАЧ ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
Электронное учебно-методическое пособие
Мероприятие 1.2. Совершенствование образовательных технологий, укрепление материально-технической базы учебного процесса
Нижний Новгород
2012
СБОРНИК ЗАДАЧ ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ. Алексеев В.Е., Киселева Л.Г.,
Смирнова Т.Г. Электронное учебно-методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2012. – 80 с.
В сборнике задач содержится краткий теоретический материал и предлагаются задачи различной степени сложности по основным разделам курса ―Дискретная математика‖: теории множеств, бинарным отношениям, комбинаторике, теории графов, алгебре логики и основам алфавитного кодирования. Раздел "Контрольные задания" представлен контрольными работами по теории множеств и комбинаторике.
Электронное учебно-методическое пособие предназначено для студентов первого курса дневного и вечернего отделений факультета ВМК, обучающихся по направлениям подготовки 010400 «Прикладная математика и информатика» и 010300 «Фундаментальная информатика и информационные технологии», изучающих курс «Дискретная математика».
2

1. Множества и операции над ними
Терминология и обозначения
{a1 , a2 ,..., an } – множество, состоящее из n элементов a1 , a2 ,..., an .
{x | P( x)} – множество, состоящее из таких элементов x , которые обладают свойством P .
x A – элемент x принадлежит множеству A .
x A – элемент x не принадлежит множеству A .
– пустое множество (не содержащее ни одного элемента).
U – универсальное множество (универс), т. е. множество всех элементов.
A B – множество A является подмножеством множества B ( A включено
в B , A содержится в |
B ), это означает, что каждый элемент множества A |
|
является элементом множества B . |
|
|
A B означает, что |
A B и |
A B , т.е. A является собственным |
подмножеством B . |
|
|
2 A {X | X A} — множество всех подмножеств A . |
||
A U A — дополнение множества A .
A B {x | x A или x B} – объединение множеств A и B .
A B A B {x | x A и x B} – пересечение множеств A и B .
A B {x | x A и x B} – разность множеств A и B .
A B ( A B) (B A) – симметрическая разность множеств A и B .
Некоторые свойства операций над множествами
1. |
A A; |
A ; |
||||
2. |
A U U ; |
A U A; |
||||
3. |
A A A; |
A A A; |
||||
|
|
|
|
|
|
|
4. |
A A U ; |
A A ; |
||||
5.A A;
6.коммутативные законы:
A B B A; |
AB BA; |
7. ассоциативные законы: |
|
|
3 |

A (B C) ( A B) C ; |
A(BC) ( AB)C ; |
|||||||||||||||||
8. |
дистрибутивные законы: |
|
|
|
|
|
|
|
|
|
||||||||
A(B C) ( AB) ( AC) ; |
A (BC) ( A B)( A C) ; |
|||||||||||||||||
9. |
законы де Моргана: |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B A B ; |
|
A B A B ; |
||||||||||||||
10. законы поглощения: |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
A A B A; |
A (A B) A; |
|||||||||||||||
|
|
|
|
|
B) AB ; |
|||||||||||||
11. |
|
A |
A |
B A B ; |
A( |
A |
||||||||||||
12.A B A B .
13.A B A B A B .
Операцию пересечения считаем более сильной, чем другие. Это означает, что при отсутствии скобок она выполняется первой. Например, формула ( AB C) CD эквивалентна (( A B) C) (C D).
1.1.Какие из следующих утверждений верны:
1) |
b {a, b}; |
5) |
b {a,{b}}; |
9) |
{ }; |
2) |
b {a,b}; |
6) |
b {a,{b}}; |
10) |
{ }; |
3) |
{b} {a,b}; |
7) |
{b} {a,{b}}; |
11) |
; |
4) |
{b} {a,b}; |
8) |
{b} {a,{b}}; |
12) |
? |
1.2.Сколько элементов в каждом из множеств:
1) |
1, 2, 3, 1, 2, 3 ; |
4) |
; |
2) |
{1,{1},2,{1,{2,3}}, }; |
5) |
, ; |
3) |
; |
6) |
, ? |
1.3.Известно, что A B и a A. Какие из следующих утверждений верны:
1) |
a B ; |
6) |
a A B ; |
2) |
a B ; |
7) |
a A B ; |
3) |
A B ; |
8) |
a A; |
4) |
a A B; |
9) |
a A; |
|
|
|
4 |
5) |
a A B; |
|
|
|
|
|
10) |
|
a B ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.4. |
Известно, что |
B A C , |
|
a A и |
a B . |
|
Какие |
из следующих |
||||||||||||||||||||||
утверждений верны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
a С ; |
|
|
|
|
|
9) |
|
a A С ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
a C ; |
|
|
|
|
|
10) |
|
a A C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3) |
a A B; |
|
|
|
|
|
11) |
|
a A C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4) |
a A B; |
|
|
|
|
|
12) |
|
a A B С ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
5) |
a A B ; |
|
|
|
|
|
13) |
|
|
|
A |
|
B |
|
C |
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6) |
a B A; |
|
|
|
|
|
14) |
|
|
|
B |
|
|
|
|
A |
; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
a |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7) |
a A B; |
|
|
|
|
|
15) |
|
|
|
A |
|
B |
|
C |
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8) |
a A C ; |
|
|
|
16) |
|
a B A C ? |
|
|
|
|
|
|
|
|
|||||||||||||||
1.5. |
Дан |
универс |
|
|
U {1,2,3,4,5,6,7,8} |
|
и |
|
|
|
его |
подмножества |
||||||||||||||||||
A {x | 2 x 6}, |
B {x | x четно} , |
C {x | x 4}, |
D {1,2,4}. Найти |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
A B , |
|
CD , B C , |
|
|
|
|
|
|
|
( A B) (C D) , |
|
|
|
|
|
, |
||||||||||||
множества |
|
A (BD) , |
|
|||||||||||||||||||||||||||
|
|
A |
B |
C |
||||||||||||||||||||||||||
2 A 2B , 2D 2B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.6. |
Дан |
универс |
|
|
U {1,2,3,4,5,6,7,8} |
|
и |
|
|
|
его |
подмножества |
||||||||||||||||||
A {x | x четно}, |
B {x | x кратно |
четырем} , |
|
|
|
C {x | x простое}, |
||||||||||||||||||||||||
D {1,3,5}. Найти множества A B , |
CD , A B , A B C D , C D , |
|||||||||||||||||||||||||||||
|
|
|
|
|
, C A D , 2 A 2B , 2 D 2C . |
|
|
|
|
|
|
|
|
|||||||||||||||||
( A B) (C D) , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
A |
B |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1.7.Пусть M 2 , M 3 , M 5 обозначают подмножества универса , состоящие
соответственно из всех чисел, кратных 2, 3, 5. С помощью операций над множествами выразить через них множества всех чисел:
1)делящихся на 6;
2)делящихся на 30;
3)взаимно простых с 30;
4)делящихся на 10, но не делящихся на 3.
Используя теоретико-множественную символику, записать утверждения:
1) 45 делится на 15;
5

2)42 делится на 6, но не делится на 10;
3)каждое число из множества {8, 9, 10} делится хотя бы на одно из чисел 2, 3, 5, но не делится на 6.
1.8.Для каждого i 1,2,..., n даны множества
Ai {(i, j) | j 1,2,..., n} |
и Bi {( j,i) | j 1,2,..., n}. |
Выразить через них с помощью операций , ,– множества:
1){(i, j) |1 i k, 1 j k, k n};
2){(i,i) | i 1,2,..., n};
3){(i, j) |1 i j n}.
1.9.Выяснить, обладают ли операции – , свойствами коммутативности и ассоциативности.
1.10.Выяснить, какие из следующих дистрибутивных законов справедливы для любых множеств A, B,C :
1)A (B C) ( A B) ( A C);
2)A (B C) ( A B) ( A C) ;
3)A (B C) ( A B) ( A C) ;
4)A B C ( A B)( A C) ;
5)A (B C) ( A B) ( A C) ;
6)A B C ( A B)( A C) ;
7)A (B C) ( A B) ( A C) ;
8)A(B C) A B AC ;
9)A (B C) ( A B) ( A C) ;
10)A (B C) A B AC ;
11)A (B C) ( A B) ( A C) ?
1.11.Доказать тождества:
1) A A B A; 10) A B A B A B ;
2) A( A B) A; |
11) |
A ( A B) B ; |
||||||||
|
A |
|
|
B A B ; |
12) |
A B A A B ; |
||||
3) |
A |
|||||||||
|
A( |
|
B) A B ; |
13) |
A B ( A B) A B ; |
|||||
4) |
A |
|||||||||
|
A ( A B) A B; |
|
|
|
|
|
||||
5) |
|
A B |
|
B A B U ; |
||||||
14) |
A |
|||||||||
|
|
|
|
|
|
6 |
|
|
|
|
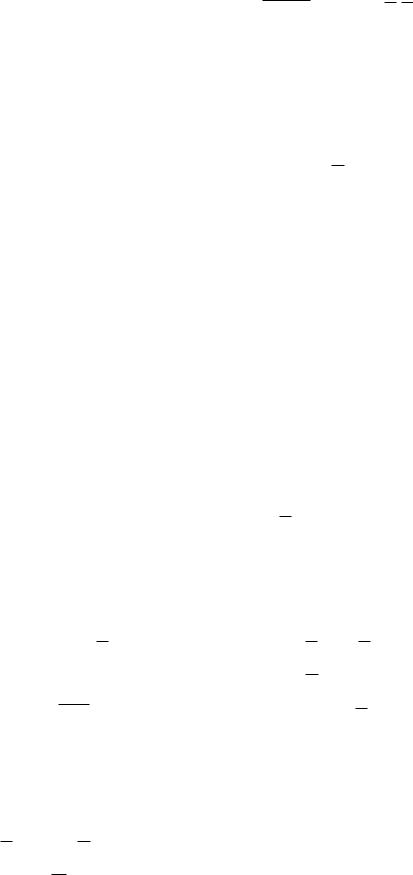
6) A A B A B ; 15) A B A B A B ;
|
A(B A) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7) |
|
A |
|
|
|
|
|
B A B ( A B) ; |
|||||||||
16) |
B |
A |
|||||||||||||||
|
A (B A) A B ; |
|
|
|
|
|
|
|
|
||||||||
8) |
|
A |
|
|
B A |
|
B B A B ; |
||||||||||
17) |
A |
A |
|||||||||||||||
|
A B A |
|
A; |
18) |
A (B C) ( A B)( A C) ; |
||||||||||||
9) |
B |
||||||||||||||||
19)( A B) C ( A C) (B C) A (B C);
20)A (B C) ( A B) AC ( A B) ( A C) ;
21)( A B) C ( A C) (B C) ;
22)A B C ( A B) (B C) (C A) ABC ;
23)A BC ( A B) ( A C) ABC A;
24)A(B C) A B C A B C A B ;
25)( AB A) (BC C) ( AB BC) ( A C);
26)( A B) (B C) ( A C) B ( AB BC) ( A C).
1.12.Выразить:
1)через , ;
2)через , ;
3)и через , – .
1.13.Доказать, что A B равносильно AB .
1.14.Доказать, что A B равносильно A B .
1.15.Упростить систему условий:
A B C B; 1) ABC D;
AD B C .
C A B;
A D B C; 3) B D C;
BC D.
A B C;
C D;
2)
AD B C D;
B CD.
7

1.16. Выяснить, равносильны ли следующие системы условий:
X Z W ,
1)Y W ,
X Y Z W
C D A,
2)B D A C,A D C B
X Z , и Y W .
A CD,
и B C A,A C D.
|
B |
|
, |
A C B , |
CD |
||
C D B, |
|||
|
|
||
3) C B D, |
и |
||
|
AC D, |
||
AC B D |
|
||
|
A B BC. |
||
1.17. Решить уравнение: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) |
A X B ; |
16) |
|
A X B X A ; |
|||||||||||||||
|
A X B ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
17) |
|
A X B ( X A) B ; |
||||||||||||||||
|
A X B ; |
|
|
|
|
|
|
|
|
|
|||||||||
3) |
18) |
|
A X B X ; |
||||||||||||||||
4) |
A X B; |
19) |
|
X A B ( X A) ; |
|||||||||||||||
5) |
A X B X ; |
20) |
( A X ) B B X A; |
||||||||||||||||
6) |
A X B X ; |
21) |
|
X A B ( X A) ; |
|||||||||||||||
7) |
A X X B ; |
22) |
( A X ) X X B ; |
||||||||||||||||
|
( A X ) B X B; |
|
|
A X |
|
( X B) B ; |
|||||||||||||
8) |
23) |
|
A |
||||||||||||||||
|
A X ( X B) A; |
|
( A X ) B |
|
B X ; |
||||||||||||||
9) |
24) |
A |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A ( X B) B X ; |
|||||||||
10) |
|
X A ( X B) A; |
25) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
B X ( A X ) X ; |
|||||||||||
11) |
( A X ) B X B ; |
26) |
|
||||||||||||||||
12) |
( A X ) B B X ; |
27) |
|
A X B X A ; |
|||||||||||||||
|
|
|
|
|
( X B) A A X ; |
||||||||||||||
13) |
( X A) B A X ; |
28) |
|||||||||||||||||
14) |
( X A) B B X ; |
29) |
|
A X B A X ; |
|||||||||||||||
15) |
|
A X B B X ; |
30) |
|
X A (B X ) A. |
||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
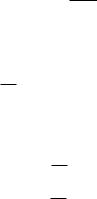
1.18. Найти множество X , удовлетворяющее системе уравнений, где A , B , C
– данные множества, B A C : |
|
|
|
A X B |
|
A X B |
|
1) |
; |
2) |
. |
A X C |
|
A X C |
|
1.19. Решить систему уравнений:
( A X )(B X ) C X
1) ;
BX C AX
AX B
B X C
3) ;
CX A B
AX B X C
5) ;
BX A X C
A B X X C
2) ;
AX B AX C
|
|
|
|
|
|
|
|
||
A X B |
|
|||
4) |
; |
|||
|
|
|
||
A X C |
|
|||
A X BX
6) .
AX C X
9

2. Бинарные отношения
Терминология и обозначения
A B a,b a A, b B – (множество всех упорядоченных пар) прямое
(декартово) произведение множеств A и B .
Любое R A B называется бинарным отношением, определенным на паре множеств А и В (далее просто отношением).
A2 A A (декартов квадрат множества А). Если R A2 , то R называется
отношением на множестве А.
x R y означает, что ( x, y) R ( x и y находятся в отношении R).
R 1 {(a,b) | (b, a) R} – отношение, обратное к R .
R1 R2 |
– произведение отношений R1 и R2 : если R1 A B , R2 B C , то |
R R1 |
R2 A C и xR y существует такой z B , что xR1 z и zR2 y . |
Важнейшие свойства отношений
Отношение R на множестве A называется
(1)рефлексивным, если для любого x A справедливо xR x ;
(2)симметричным, если из xR y следует yR x ;
(3)антисимметричным, если из xR y и yR x следует x y ;
(4)транзитивным, если из xR y и yR z следует xR z .
|
Рефлексивное, симметричное и транзитивное отношение называется |
отношением эквивалентности (или просто эквивалентностью). |
|
|
Рефлексивное, антисимметричное и транзитивное отношение называется |
отношением порядка (или просто порядком). Порядок R на множестве A |
|
называют линейным, если для любых x, y A имеет место xR y или yR x . |
|
2.1. |
Пусть A {1, 2, 3} и B {a, b}. Определите A B, A A, B A, B B, |
A , 2 A , 2 B , B 2 B . |
|
2.2. |
Пусть A , B { } и C { ,{ }}. Определите A B, A C, B C, |
B B, C C , 2 A , 2 B , 2C , B 2 B , B 2C , C 2 B .
10
