3.4. Параметры струйки и гидравлическое уравнение неразрывности

Площадь поперечного элементарно малого сечения струйки жидкости называется живым сечением. Живое сечение нормально к линиям тока (рис. 3.2).

Рис. 3.2. Элементарная струйка

Скорость движения частиц в живом сечении - скорость струйки .

Расстояние вдоль струйки при известной скорости струйки .

За определенное время движущиеся частицы из сечения 1-1 переместятся в сечение 2-2, пройдя путь, равный .

Таким образом, за время через первое живое сечение площадью пройдет количество жидкости, равное объему элементарного цилиндра:

.

Объем жидкости, отнесенный к единице времени , - объемный расход (элементарный расход), который определяется по формуле, м³/с,

(3.9)

Количество жидкости, проходящей через живое сечение, можно представить через массу и вес жидкости.

Массовый расход струйки, кг/с,

(3.10)

Весовой расход струйки, Н/с,

(3.11)

Расходом жидкости называется количество жидкости, проходящей через живое сечение за единицу времени.

Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении (рис. 3.3). Выделим в элементарной струйке объем между двумя сечениями 1-1 и 2-2 в некоторый момент времени. Используем свойства элементарной струйки и закон сохранения вещества (массы).

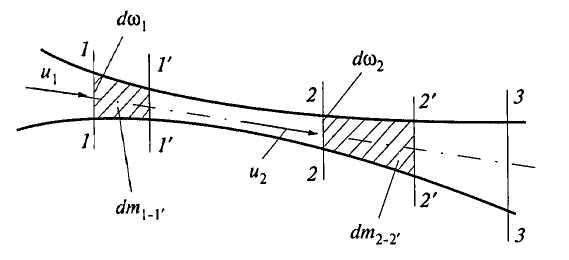
Рис. 3.3. К выводу уравнения неразрывности

За время масса жидкости , находящаяся между сечениями 1-1 и 2-2, переместится в положение 1'-1' и 2'-2'.

Массы жидкости между сечениями

где и - элементарные массы жидкости, проходящие через сечения 1-1 и 2-2.

Масса жидкости остается неизменной при ее перемещении:

Следовательно, Масса жидкости, проходящая через любое сечение, равна

.

Масса жидкости, проходящая через первое и второе сечения струйки за время , составляет

где - плотность жидкости, находящейся в трубке тока.

Таким образом,

(3.12)

Аналогично можно получить соотношение скоростей и элементарных площадей для других сечений струйки.

Например,

Таким образом, для любого сечения струйки .

Уравнение неразрывности для элементарной струйки при установившемся движении утверждает, что элементарный расход во всех сечениях струйки постоянен.

Уравнение неразрывности записывается в следующем виде:

(3.13)

Скорости движения в разных сечениях струйки согласно (3.13) обратно пропорциональны элементарным площадям живых сечений струйки:

(3.14)

где - произвольное живое сечение струйки, скорость струйки в нем .

3.5. Поток жидкости и его параметры

Согласно струйчатой модели поток жидкости - совокупность элементарных струек. Сечение потока , ограниченного конечными поверхностями, равно сумме живых сечений струек . Это сечение называется живым сечением потока жидкости. Живое сечение должно быть нормальным к векторам скорости струи , т.е. нормально к линиям тока:

. (3.15)

Общий объемный расход жидкости для потока жидкости в целом будет представлять собой сумму элементарных расходов струек:

. (3.16)

Расход жидкости можно представить в виде объемной фигуры, ограниченной, например, параболой, основание которой будет площадь живого сечения (рис. 3.4).

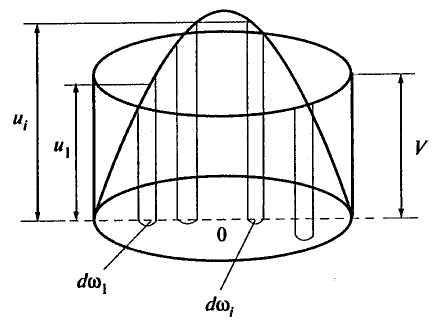
Рис. 3.4. К определению средней скорости

Объем этой фигуры .

Чтобы определить расход, необходимо иметь аналитическую зависимость значения скорости от конечного положения элементарной площади струйки . Скорость струйки является функцией координат : . В связи с этим представляется весьма сложным произвести интегрирование уравнения расхода (3.16).

Для упрощения определения расхода потока жидкости вводится понятие о средней скорости. Принимается условие, что скорости струек по всему живому сечению потока постоянны, . Таким образом, все частицы жидкости, проходящие через площадь , имеют одинаковую скорость .

Объему фигуры, ограниченной параболой вращения, соответствует объем цилиндра, высота которого равна средней скорости:

(3.17)

Если живое сечение струек будет нормальным к вектору скорости в сечении потока жидкости, тогда элементарные струйки (линии тока) представляются в виде системы прямых параллельных друг другу линий, а живые сечения являются плоскими.

Движение жидкости, при котором имеет место некоторое расхождение линии тока (струек), что характеризуется малым углом и незначительной кривизной, называется плавно изменяющимся движением.

В случае плавно изменяющегося движения можно считать живые сечения плоскими, нормальными к вектору скорости.

На рис. 3.5 показано живое сечение цилиндрической трубы, по которому движется поток воды со средней скоростью , вектор которой нормален к поперечному сечению.

Рис. 3.5. Гидростатический напор в плоскости живого сечения

К точкам 1, 2, 3 поперечного сечения трубы присоединены пьезометры. Положение точек относительно плоскости сравнения 0-0 - ,, и. Пьезометрические высоты - , , имеют разные значения.

Сумма величин и , определяющих гидростатический напор, постоянна, т.е.

Таким образом, для любой точки живого сечения гидростатический напор относительно выбранной плоскости сравнения постоянен:

Установившееся движение, при котором поперечные сечения потока и средняя скорость в них одинаковы, называется равномерным движением. Примерами равномерного движения могут служить движения воды в трубе постоянного диаметра или в канале с постоянной глубиной и формой поперечного сечения.

Неравномерным называют установившееся движение, при котором поперечное сечение и средняя скорость изменяются по длине потока. Движение воды в трубе переменного диаметра является неравномерным.

Движение потока жидкости может быть напорным или безнапорным. При напорном движении поток ограничен твердыми поверхностями и жидкость полностью заполняет поперечные сечения по его длине. Поток жидкости не имеет свободной поверхности, и движение происходит за счет перепада напоров по длине.

Безнапорным движением называют движение, когда поток частично ограничен твердой поверхностью и имеет свободную поверхность. В большинстве случаев свободная поверхность граничит с атмосферой. Давление на свободную поверхность в этом случае будет равно атмосферному - . Примером может служить движение в трубах с не полностью заполненными поперечными сечениями или поток в канале, реке.

Гидравлические элементы потока жидкости

Контур живого сечения, соприкасающегося с твердой поверхностью стенки, называется смоченным периметром . Для круглой трубы смоченный периметр равен периметру живого сечения.

Гидравлический радиус представляет собой отношение площади живого сечения к смоченному периметру :

(3.18)

Гидравлический радиус характеризует форму живого сечения потока жидкости.

Гидравлический диаметр

. (3.19)

Для круглой трубы диаметром при напорном движении

(3.20)

При напорном движении в трубе прямоугольного сечения (шириной , высотой )

(3.21)

Для безнапорного движения жидкости в прямоугольном канале с шириной по дну , глубиной жидкости