Глава 3. Основы кинематики и динамики жидкости

3.1. Задачи кинематики и динамики

Жидкая среда состоит из множества ее частиц, не связанных между собой, и при ее движении частицы перемещаются в пространстве независимо друг от друга. Жидкая среда является сплошной средой, в которой отсутствуют пустоты и разрывы. Скорость в определенной точке области, занятой жидкостью, а также плотность и давление являются функцией координат этой точки и времени.

Кинематика изучает характеристики движений жидкости и газов. Задачей кинематики является определение скоростей и ускорений в любой точке пространства жидкой среды и распределение скоростей. Для упрощения исследования движения жидкость полагают идеальной и однородной. В этом случае не учитываются силы, обусловленные вязкостью.

Динамика жидкости изучает законы движения в результате действия на нее поверхностных, массовых сил с учетом вязкости.

Основными задачами в динамике являются рассмотрение движения жидкости в трубах, открытых руслах и в гидросооружениях, а также задачи, связанные с обтеканием жидкостью твердых тел и движением тела в жидкости.

При исследовании движения реальной жидкости необходимо рассматривать возникновение и влияние касательных напряжений, т.е. сил сопротивления движению. Если скорости и давления в определенной области будут зависеть от одной из координатных осей, то такие движения называются одномерными. В случае, когда скорости зависят от двух или трех координат, движения являются двухмерными или трехмерными.

При исследовании жидкости используются следующие схемы (модели):

• струйчатая схема (модель) движения. Поток жидкости с целью упрощения рассматривается в виде движения множества отдельных элементарных струек;

• модель движения множества частиц жидкости образует сплошную среду. В этом случае рассматривается движение отдельных частиц и течение жидкости представляется в виде дифференциальных уравнений, которые отражают основные кинематические и динамические характеристики.

3.2. Аналитические методы исследования движения жидкости

Существует два аналитических метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

Метод Лагранжа

Метод Лагранжа изучает кинематику движения в пространстве какой-либо частицы жидкости. Координаты частицы в начальный момент времени :,,. Движущаяся частица имеет определенные текущие координаты ,,, которые фиксируются относительно начальных координат ,,. Кинематическая картина движения частицы определяется следующими функциональными зависимостями:

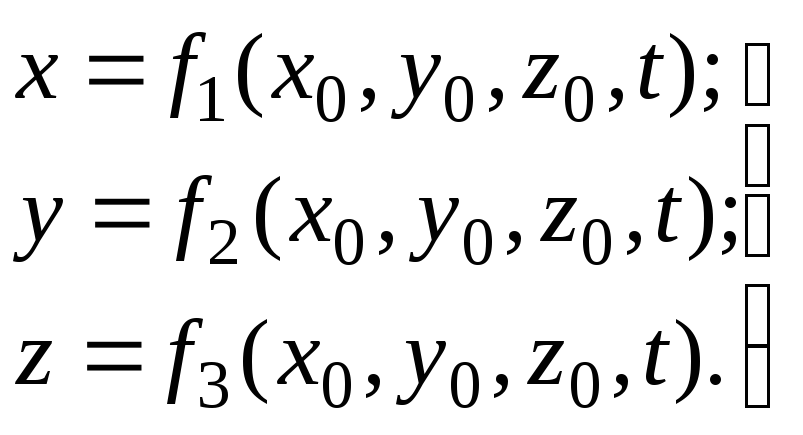(3.1)

Зная текущие координаты частицы, можно построить ее траекторию движения в определенной области пространства. Имея траекторию движения, можно разбить ее на малые участки длиной , проходимые частицей за время . Проекции скорости в точке, где находится частица:

(3.2)

Величины , , являются проекциями пути движения частицы на участке траектории за время на соответствующие координаты.

Поток жидкости будет характеризоваться траекториями движения определенных частиц в течение определенного времени. Метод Лагранжа в технической гидромеханике из-за его сложности не получил достаточно широкого применения.

Метод Эйлера

Метод Эйлера изучает определенную область движения жидкости. В этой области пространства фиксируются точки, которые являются неподвижными при прохождении через них жидкости. В этом случае не рассматриваются траектории движения частиц, как в методе Лагранжа. Метод Эйлера позволяет исследовать изменение скоростей, ускорений в разных точках выбранной области пространства жидкости. Скорости рассматриваются относительно неподвижной системы координат. Составляющие абсолютной скорости , , зависят от нахождения точки в пространстве, т.е. от координат ,, и времени .

Составляющие скорости выражаются следующими функциональными зависимостями:

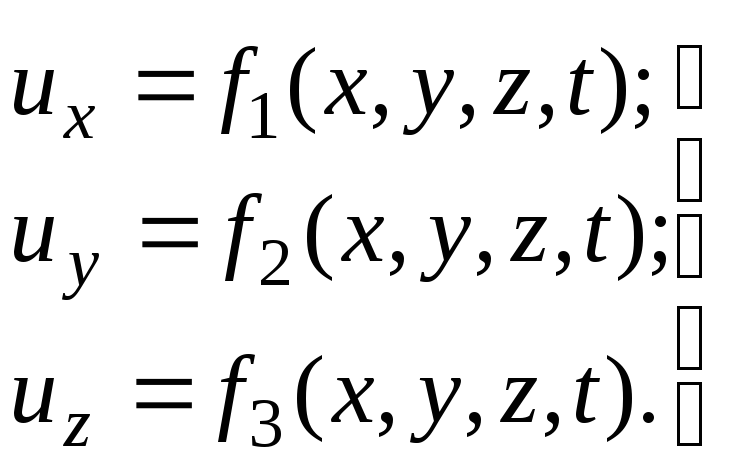(3.3)

Следует отметить, что давление в точке также является функцией координат:

(3.4)

Метод Эйлера позволяет получить распределение скоростей в определенной области. В случае движения жидкости, когда скорости частиц, проходящих через определенную точку в пространстве, зависят не только от координат расположения точки , но и времени (формула (3.3)), такое движение называется неустановившимся (нестационарным).

Установившимся (стационарным) движением является движение, когда скорости в точке не зависят от времен. Зависимости, определяющие скорости, в этом случае выглядят так:

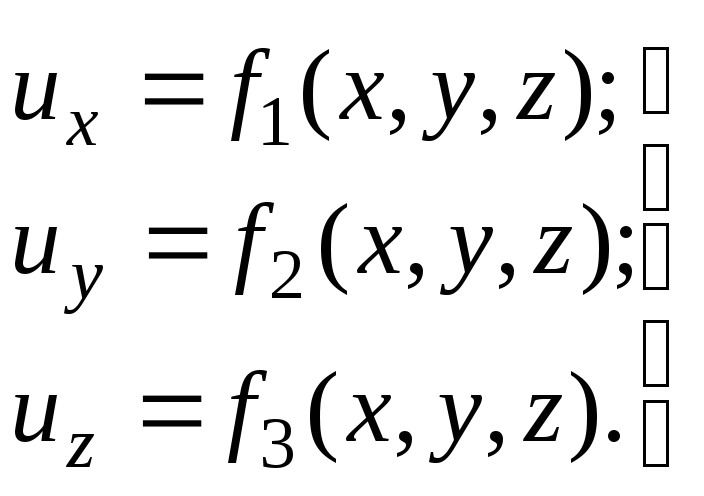(3.5)

Так как абсолютная скорость является функцией координат и времени , то полный дифференциал скорости в местных производных

(3.6)

Абсолютное ускорение в точке

(3.7)

Составляющие скорости

(3.8)

При исследовании движения жидкости по методу Эйлера ее геометрическими характеристиками являются линии тока.

Частичка жидкости при движении может изменять свою форму при сохранении своего объема и массы. Частица может двигаться поступательно или вращательно, при этом по сравнению с твердым телом она деформируется.