Лекция 5. Вихревое движение жидкости
5.1. Циркуляция и вихревое движение несжимаемой жидкости
Особенностью движения жидкости на криволинейных участках является возможность образования циркуляционного течения. Пусть поле скоростей жидкости искривлено (рис. 5.1, а).
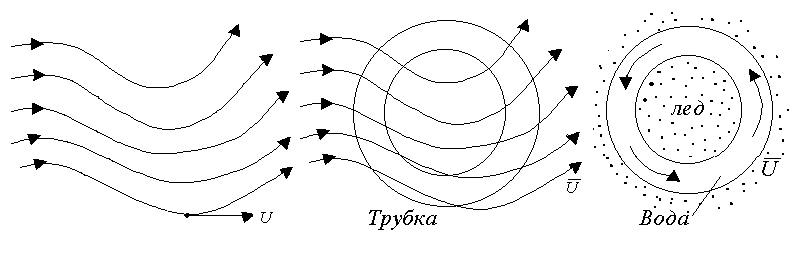
Рис. 5.1. Образование циркуляции в поле скоростей жидкости
Поместим в жидкость замкнутую трубку в виде петли постоянного сечения. При мгновенном замораживании жидкости, находящейся вне трубки, в ней сохранится импульс. Жидкость будет двигаться и приобретет циркуляцию равную произведению средней касательной компоненты скорости на длину контура обхода.
Если в жидкости провести отрезок кривой АВ (рис. 5.2), то криволинейный интеграл в векторном поле скоростей равен
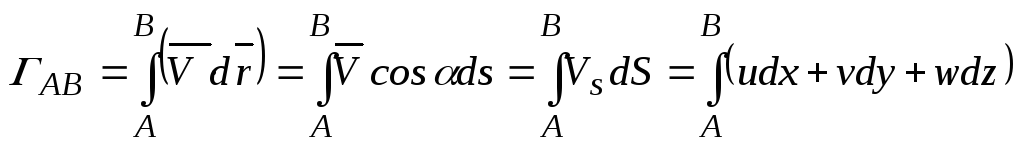(5.1)
и определяет циркуляцию скорости на участке АВ.
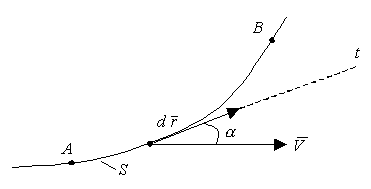
Рис.5.2. Определение циркуляции скорости на участке АВ незамкнутого контура
Для замкнутого контура запишем
.
(5.2)
Рассмотрим вращение твердого тела (рис. 5.3)
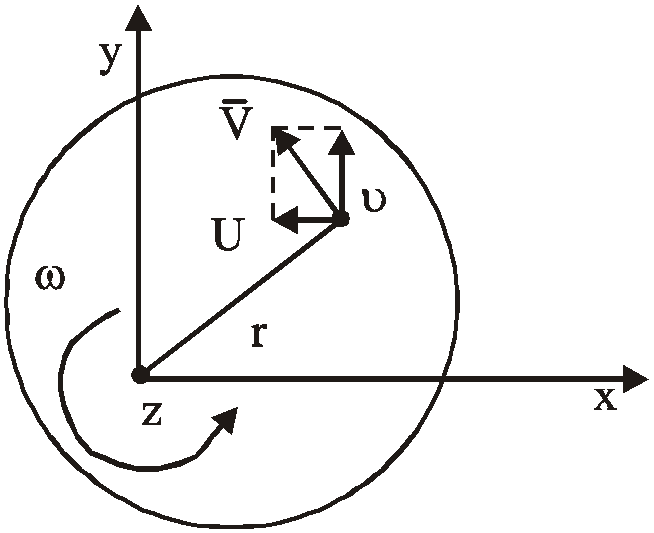
Рис.5.3. Вращение твердого тела
Если
угловая скорость вращения
относительно оси Z,
то скорость точки тела
М равна
а ее проекции на оси X
и Y
будут
(5.3)
Определив
значения
и
получим величину завихренности
(5.4)
т.е.
-компонента
вектора завихренности связана с
-компонентой
вектора угловой скорости вращения
жидкой частицы
соотношением
Аналогично можно получить компоненты
(5.5)
Вихрь
вектора скорости жидкой частицы
определяется через вектор угловой
скорости
(5.6)
Вихревое движение может быть и ламинарным и турбулентным.
5.2. Потенциальное движение несжимаемой жидкости
Если
то течение становится потенциальным
(безвихревым). При этом будет выполняться
условие
(5.7)
что
возможно при существовании функции
удовлетворяющей условиям:
(5.8)
Такое течение называется потенциальным. В этом случае циркуляция скорости на участке АВ определяется разностью потенциалов скоростей в точках А и В:
(5.9)
5.3. Вихревые линии и вихревые трубки
Вихри скоростей образуют вихревое поле, в котором находятся вихревые линии и вихревые трубки. Из определения вихревой линии и вихревой трубки следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.
Вводя понятие потока вектора вихря скорости, равного
(5.10)
где
- площадь поверхности;
- нормаль к поверхности, найдем, что
поток вектора вихря скорости через
вихревую поверхность будет равен нулю:
(5.11)
Поток вектора вихря скорости сквозь произвольное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки (рис. 5.4):
(5.12)
Рис.5.4. Вихревая трубка
Это утверждение составляет вторую теорему Гельмгольца.
Поток вихря характеризует интенсивность вихревой трубки
(5.13)
При
постоянной величине вихря
получим
(5.14)
откуда следует:
1) сечение вихревой трубки нигде не может стать равным нулю, т.к. бесконечно большая скорость вращения частиц физически невозможна;
2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца, либо «опираются» на стенку или на свободную поверхность.
Другой важной теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру один раз опоясывающему вихревую трубку, т.е.
(5.15)
где
-
длина контура.