Контрольные вопросы

1. Как вы понимаете оптимальность, применительно к данной задаче?

2. В чём экономический смысл целевой функции?

3. В чём состоит экономический смысл ограничений?

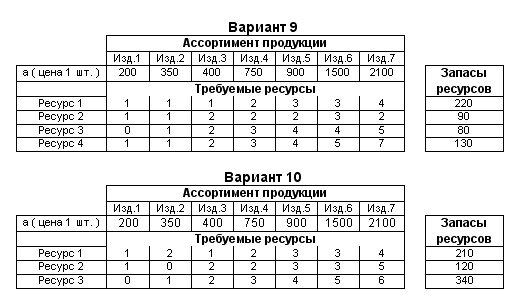
Варианты заданий к лаб. раб.№2

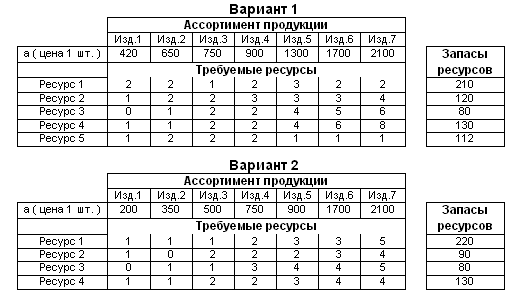
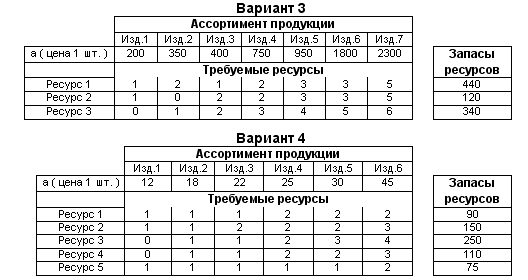
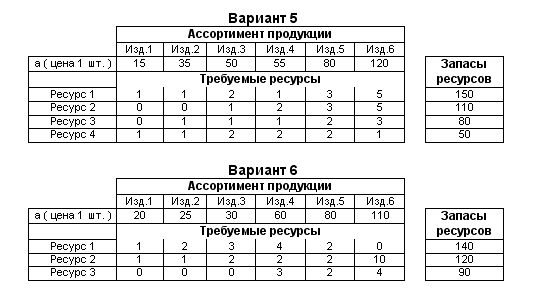
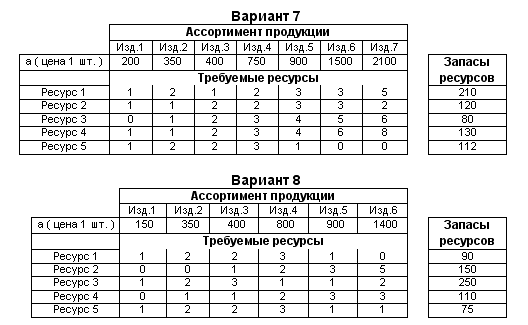
Практическая работа № 3 определение парных коэффициентов корреляции

Цель работы. Познакомиться с экономическим смыслом парных коэффициентов корреляции. Освоить математический инструментарий их нахождения. Исследовать результаты наблюдений на предмет их пригодности для моделирования производственной функции.

Пример решения задачи

Исходные данные

Допустим, в результате наблюдений за процессом была получена исходная информация с целью нахождения производственной функции. Перед моделированием следует проверить параметры х₁, х₂, х₃ на мультиколлинеарность и выявить уровень их значимости для Y.

№ п/п	х1	х2	х3	Y
1	2	7	5	45
2	18	6	26	80
3	14	17	31	134
4	15	16	33	190
5	6	17	14	170

Создание матрицы отклонений от среднего:

Найти среднее арифметическое значение каждого столбца.

Отнимая от каждого элемента столбца соответствующее среднее значение, получим матрицу отклонений от среднего:

№ п/п	х1- х1ср	х2- х2ср	х3- х3ср	Y- Yср
1	-9	-5,6	-16,8	-78,8
2	7	-6,6	4,2	-43,8
3	3	4,4	9,2	10,2
4	4	3,4	11,2	66,2
5	-5	4,4	-7,8	46,2

Каждый из 4-х столбцов полученной матрицы можно рассматривать как многомерный вектор. В связи с этим, все дальнейшие действия по определению парных коэффициентов корреляции рассматривают как нахождение косинусов углов между любыми двумя векторами.

Например, даны два вектора А(а₁;а₂) и В(b₁;b₂). Косинус угла между ними равен результату от деления скалярного произведения данных векторов на произведение их модулей:

Cos φ=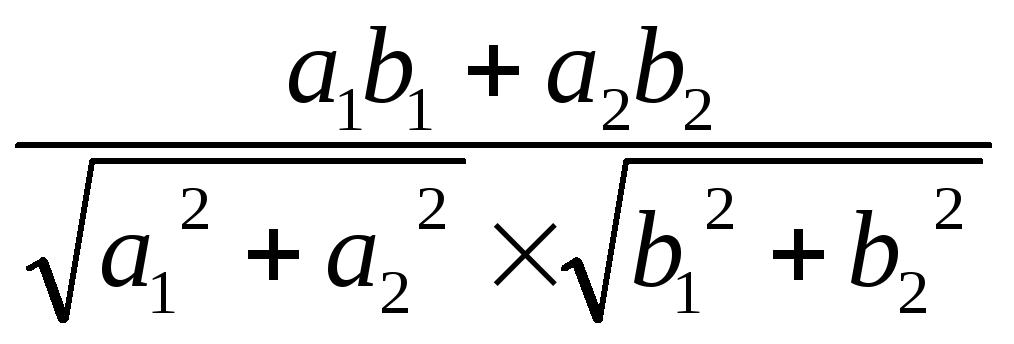

Вычисления упростятся, если векторы будут нормированы (приведены к векторам с единичным модулем). В этом случае знаменатель дроби будет равен 1 и Cos φ будет равен скалярному произведению векторов.

Нормирование матрицы отклонений от среднего

Найти модули всех 4-х векторов по формулам:

│х₁- х_1ср│=≈13,42

│х₂- х_2ср│=≈11,19

│х₃- х_3ср│=≈23,89

│Y- Y_ср│=≈121,44

Разделив каждый элемент столбца матрицы отклонений на соответствующее значение модуля, получить нормированную матрицу отклонений. В геометрической интерпретации каждый из 4-х столбцов представляет собой многомерный вектор, «длина» которого равна 1. Поэтому, в обозначениях столбцов полученной матрицы нормированных отклонений используют индекс 0.

№ п/п	х01	х02	х03	Y0
1	-0,67	-0,50	-0,70	-0,65
2	0,52	-0,59	0,18	-0,36
3	0,22	0,39	0,39	0,08
4	0,30	0,30	0,47	0,55
5	-0,37	0,39	-0,33	0,38

Вычисление парных коэффициентов корреляции

Вычисление парных коэффициентов корреляции сводится к скалярному произведению пар полученных нормированных векторов:

rх0₁х0₂=≈0.06

rх0₁х0₃=≈0.91

rх0₁Y₀=≈0.29

rх0₂х0₃=≈0.41

rх0₂Y₀=≈0.89

rх0₃Y₀=≈0.56

Используя таблицу определения критических значений коэффициента парной корреляции, можно сформулировать вывод о том, что гипотеза наличия линейной связи между парами входных факторов и выходного результата не подтверждена (обязательно разберитесь, почему, и обоснуйте в выводе к лабораторной работе)

На основании полученных значений парных коэффициентов корреляции, можно сделать вывод:

• по признаку значимости ни одним из параметров нельзя пренебречь, т. к. 0,29›0,05; 0,89›0,05; 0,56›0,05;

• между параметрами х₁ и х₃ наблюдается мультиколлинеарность, т. к. 0,91›0,88. При моделировании влияние каждого из этих параметров, в отдельности, будет определить достаточно сложно, поэтому один из них должен быть удален из процесса моделирования, либо параметры х₁ и х₃ должны быть объединены в один.

Указания к выполнению работы

9. Среднее арифметическое каждого из столбцов матрицы исходных данных удобно найти с помощью функции СРЗНАЧ.

10. Для определения модуля каждого из векторов отклонений удобно использовать функции СУММКВ (сумма квадратов) и КОРЕНЬ.

11. На этапе вычисления парных коэффициентов корреляции нужно попарно скалярно умножить векторы. Умножение сразу всех векторов можно сделать, умножив нормированную матрицу отклонений на транспонированную. Результатом будет являться матрица, содержащая все парные коэффициенты корреляции. Диагональ полученной матрицы будет заполнена единицами. Косинус угла между совпадающими векторами равен 1.

	х01	х02	х03	Y0
х01	1	0,06	0,91	0,29
х02	0,06	1	0,41	0,89
х03	0,91	0,41	1	0,56
Y0	0,29	0,89	0,56	1

12. Парные коэффициенты корреляции можно также найти с помощью функции КОРРЕЛ из категории статистических.