Построение графика функции
Используя алгоритм поиска решения, вы должны задать диапазоны значений переменной x в которых будет осуществляться поиск точных значений экстремумов. Поэтому, для наглядности, следует обязательно построить график исследуемой функции. Выбрав удобный для вашего варианта задания диапазон x и шаг, постройте график. С целью экономии места на листе, данные для построения графика оформляйте в виде столбцов.
В данном случае удобно выбрать x, меняющийся от -5 до 5 с шагом 0,5.
На графике хорошо видно, что при x ≈ -1,5 функция имеет максимум, а при x ≈ 2,5 — минимум. Таким образом, диапазон поиска максимума можно ограничить значениями -2 ≤ x ≤ -1, а минимума — 2 ≤ x ≤ 3
Решение
После того, как границы поиска экстремумов определены, формулы целевых функций составлены, из всплывающего меню «Сервис» вберите пункт «Поиск решения...». Возникнет окно «Поиск решения» .
В качестве целевой ячейки поиска решения, курсором мыши укажите ячейку целевой функции «Максимум». После этого, в поле ввода «Установить целевую ячейку» появится абсолютная ссылка на неё, в данном случае С30 (см. рисунок ниже). Убедитесь в том, что точечный переключатель установлен на поиск максимального значения целевой ячейки.
Потом установите текстовый курсор в окно «Изменяя ячейки» и с помощью мыши укажите ячейку, в которой будет найдено значение x, соответствующее максимуму функции (D30).
Теперь нужно указать границы поиска максимума. Для этого воспользуйтесь текстовой кнопкой «Добавить» в рамке «Ограничения». Используя возникшее окно «Добавление ограничения», укажите, что значение в изменяемой ячейке (в данном случае D30) не должно выходить за пределы диапазона поиска. В данном случае, первое ограничение устанавливает, что D30 ≤ -1, а второе — D30 ≥ -2.
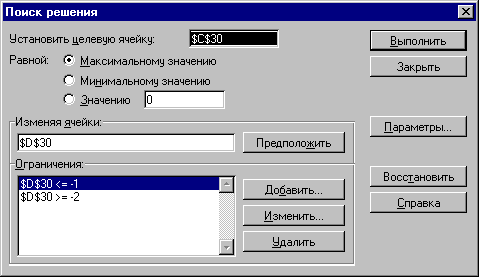
Когда все приготовления будут сделаны (указана ячейка целевой функции, изменяемая ячейка и границы диапазона поиска), нажмите кнопку «Выполнить». В результате будет найдено максимальное значение целевой функции, и соответствующее значение x.
Аналогичным способом найдите точку минимума функции. В результате решения задачи будут найдены значения функции в точках экстремумов и соответствующие значения x. На основании полученных результатов сделайте вывод.
Контрольные вопросы
Для чего можно использовать алгоритм поиска решения? К чему сводится его работа?
Что такое целевая функция?
Что такое изменяемая ячейка?
Что такое ограничение?
Можно ли при решении рассмотренной здесь задачи указать границы поиска минимума функции от -5 до 5? Почему?
Задания для самостоятельного выполнения:
Решить задачу определения минимума и максимума заданной функции
-
№ варианта
Исследуемая функция
1
y=(x-2)(x -3)(x+3)
2
y=(x+5)(x+1)(x-4)
3
y=x3+2x2-6x+9
4
y=-x3+8x2-5x-7
5
y=-x3-9x2-4x+15
6
y=(6-x)(x+4)(x-3)
7
y=(7-x)(4-x)(x+5)
8
y=х(x-2)(x+5)
9
y=х(3-x)(7-x)
10
y=х(2x+2)(4-x)